3. Равнопеременное вращение.

Вращение тела называется равнопеременным, если его угловое ускорение постоянно .

.

.

,

,

.

.

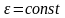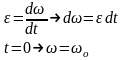
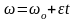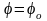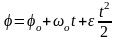Эти формулы получены для равноускоренного вращения. В случае равнозамедленного движения в формуле перед 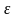стоит знак минус.

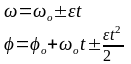
4. Линейные скорости и ускорения точек вращения.

Ввиду того, что при вращении тела его отдельные точки движутся неодинаково, представляет интерес определение их кинематических характеристик.

Рассмотрим тело, вращающееся вокруг неподвижной оси (Рис. 5).

Рис. 5

Выберем неподвижную точку А, которая движется по окружности радиуса R.

Через некоторый промежуток времени точка А переместится по окружности в А₁ на величину дуговой координаты S, а радиус R повернется на угол φ. Тогда,

.

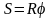Продифференцируем по t:

.

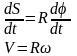Т.к. , то линейные скорости точек пропорциональны их расстояниям от оси вращения, направлены по касательной к траектории, следовательно – перпендикулярно радиусу.

Т.к. движение по окружности есть частичный случай криволинейного движения, то при вращении тела, его точки будут обладать касательным и нормальным ускорениями.

.

.

Лекция № 8 плоскопараллельное движение твердого тела

1. Определение и уравнения плоскопараллельного движения

2. Скорости при плоском движении

3. Векторная формула ускорения плоского движения

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 111 – 124.

1. Определение и уравнения плоскопараллельного движения.

Плоским называется движение тела, при котором все его точки движутся в параллельных плоскостях. Поступательное и вращательное движение относительно неподвижной оси, являются частными случаями плоского движения.

Рассмотрим тело, совершающее плоское движение. Пересекая тело неподвижной плоскостью Р, получим в сечении фигуру S (Рис. 6).

Рис. 6

Из определения плоского движения следует, что фигура S, перемещаясь вместе с телом, все время должна оставаться в плоскости Р, а точки, лежащие на линии АВ, должны двигаться так же, как и точка С. Следовательно, для изучения плоского движения тела достаточно рассмотреть движение только одной плоской фигуры.

Пусть плоская фигура движется в неподвижной системе координат xoy.

Выберем в произвольной точке С фигуры, которую назовем полюсом, начало координат системы x₁cy₁, неизменно связанной с фигурой и двигающейся вместе с ней. Положение фигуры в неподвижной системе координат будет полностью определяться положением системы x₁c y₁ , т.е. параметрами x_c и y_c,, характеризующими положение полюса, и углом φ поворота и вокруг полюса.

Таким образом, будем иметь:

.

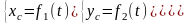1) 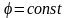, т.е. во время движения оси подвижной системы координат остаются параллельными осями неподвижной системы. Следовательно, в этом случае плоская фигура совершает только поступательное движение.

2) 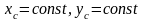, т.е. фигура совершает только вращательное движение, поворачиваясь на угол вокруг полюса С.

Таким образом, плоское движение можно представить как сочетание поступательного движения вместе с произвольно выбранным полюсом и вращательного движения вокруг полюса. В общем случае, эти движения совершаются одновременно.

Докажем, что поступательная часть движения зависит от выбора полюса, а вращательная не зависит.

Положение плоской фигуры вполне определяется положением двух ее точек или отрезка прямой, соединяющей эти точки (Рис. 7).

Рис. 7

Рассмотрим отрезок АВ и его новое положение А₂В₂. Перемещение из положения АВ в положение А₂В₂ будем рассматривать как сочетание как поступательного и вращательного движения.

Выберем за полюс точку А. Тогда, в результате поступательного перемещения вместе с полюсом отрезок АВ займет положение А₂В_1, а в результате вращательного движения вокруг полюса повернется по часовой стрелке на угол 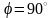до положения А₂В_2.

Выберем теперь за полюс точку В. Тогда, в результате поступательного перемещения вместе полюсом отрезок АВ займет положение А₁В₂ , а в результате вращательного движения вокруг полюса, повернется по часовой стрелке на угол до положения А₂В₂ .

Таким образом, в первом случае поступательное перемещение равно отрезку АА₂ , а во втором ВВ₂ , т.е. различно в зависимости от выбора полюса. Вращательная же часть в обоих случаях одинакова, равна по величине и направлению одному и тому углу и, следовательно, от выбора полюса не зависит.