Раздел 2. Кинематика

Тема 4. Кинематика точки лекция № 6 основные понятия кинематики. Кинематика точки

1. Основные понятия кинематики

2. Способы задания движения (векторный, координатный, естественный)

3. Взаимосвязь способов задания движений

4. Равнопеременное движение точки

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 85 – 100.

1. Основные понятия кинематики

Кинематика изучает механическое движение, под которым понимают перемещения тел относительно друг друга. При этом не рассматриваются причины, вызывающие движении, а рассматривается лишь геометрическая сторона явления.

Всякое движение тела в пространстве – относительно, т.к. оно может наблюдаться лишь по отношению к каким-либо другим телам. Такие тела и связанные с ними системы координат в механике называют системами отчета; они могут быть движущимися или условно неподвижными. Абсолютно неподвижных тел в природе не существует.

Основными кинематическими характеристиками движущегося тела являются: уравнение движения по траектории, скорость и ускорение как всего тела, так и различных его точек. Все кинематические величины рассматривают как функции времени. При этом пространство считается однородным и трехмерным, а время – непрерывным и одинаково протекающим во всех точках пространства.

Под траекторией понимают линию, которую описывает тело при своем движении в выбранной системе отсчета. По виду траектории движение можно разделить на прямолинейное и криволинейное.

Векторная величина, характеризующая быстроту и направление движения, называется скоростью.

Векторная величина, характеризующая быстроту изменения направления и модуля скорости, называется ускорением.

Все тела можно рассматривать как совокупность материальных точек. Материальная точка – точка, обладающая массой, способностью двигаться и взаимодействовать, если размерами тела можно пренебречь.

2. Способы задания движения.

Движение точки считается заданным, если в любой момент времени можно указать ее положение на траектории, определить скорость и ускорение. Существует несколько способов задания движения.

2.1. Векторный способ

При векторном способе задания движения точки ее положение на траектории в любой момент времени определяется радиус-вектором, проведенным из неподвижного центра (Рис. 1).

Рис. 1

,

,

.

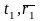
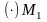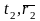
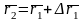Вектор 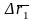характеризует изменение вектора 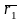за время 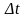по величине и направлению, т.е. определяет перемещение точки за время и называется вектором перемещения.

Уравнение движения в векторной форме записывается в виде: . Оно позволяет в любой момент времени определить положение движущейся точки по соответствующему радиус-вектору.

Для нахождения скорости точки, рассмотрим два ее положения на траектории (Рис. 2).

Рис. 2

- ,

- ,

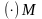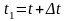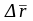- перемещение .

Средняя скорость точки, как характеристика быстроты изменения ее положения на траектории за время , может быть найдена по формуле:

,

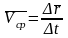т.к. , следовательно .

Устремляя к 0, найдем мгновенное значение скорости в виде:

.

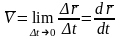Вектор скорости 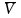будет направлен в сторону движения точки по касательной к траектории.

Для определения ускорения точки рассмотрим два ее положения на траектории (Рис. 3):

Рис. 3

Найдем . Чтобы определить величину и направление , перенесем 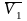в (·) 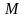и построим векторный параллелограмм, считая его диагональю.

Найдем мгновенное ускорение точки:

.

Это уравнение отражает векторную производную, которая учитывает изменение скорости как по величине, так и по направлению.

Вектор ускорения 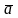располагается в плоскости кривизны траектории с направлением в сторону ее вогнутости.

Этот метод более употребителен в теоретических исследованиях.

2.2. Координатный способ.

Координатный способ задания движения применяется тогда, когда траектория движения точки заранее неизвестна. В этом случае положение точки на траектории определяется ее координатами (Рис. 4)..

Рис 4.

где 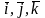- орты.

Известно, что любой вектор можно представить в виде суммы трех векторов, в данном случае через его составляющие по осям x, y, z.

.

Т.к. проекции радиус-вектора на оси равны координатам x, y, z точки , то будем иметь:

.

При перемещении точки по траектории будут изменяться во времени и ее координаты.

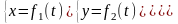– параметрическая форма записи уравнений.

Для получения уравнения траектории движения точки в координатной форме, необходимо из полученных уравнений исключить время.

Найдем выражение для скорости точки :

,

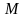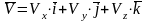где - проекции вектора скорости.

.

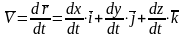Сравнивая эти выражения, получим:

.

Т.е. проекции скорости равны первым производным по времени от соответствующих координат.

Модуль скорости определится:

,

а ее направление – через направляющие косинусы:

;

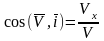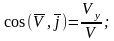
Получим теперь выражение для ускорения точки

,

.

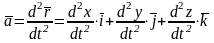Сравнивая полученные выражения, получим:

.

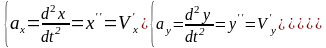Модуль ускорения:

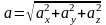
Направление ускорения:

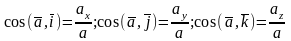
2.3. Естественный способ.

Этот способ применим, когда заранее известна траектория движения точки. В этом случае положение точки на траектории может быть охарактеризовано дуговой координатой (Рис. 5):

.

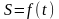Рис. 5

Дуговая координата характеризует только положение точки на траектории движения, а не пройденный путь:

Скорость: .

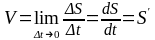Знак скорости определяет направление движения точки.

Ускорение может быть представлено в виде суммы двух составляющих (Рис. 6):

Рис. 6

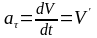- касательное ускорение,

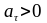- ускоренное движение,

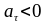- замедленное движение,

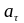- характеризует изменение скорости по величине.

нормальное ускорение,

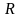- радиус кривизны траектории,

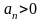- всегда,

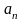- изменяет скорость по направлению,

,

.
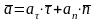
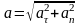