Для однородного тела во всех его точках плотность одинакова.

В этом случае в формулах  и g, как общие множители, выносится за знак суммы и сокращается с  и g в знаменателе. В результате из формул получим

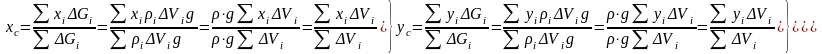
где - объем тела.

Из уравнений следует, что положение центра тяжести однородного тела зависит только от его геометрической формы, а от величины  не зависит.

Поэтому точку С, координаты которой определяются вышеуказанными формулами называют центром тяжести объема V.

Если тело представляет собой материальную поверхность, то

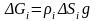
Здесь 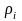- поверхностная плотность;

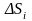- элемент поверхности, выраженный в единицах площади.

Путем аналогичных рассуждений легко найти, что если тело представляет собой тонкую однородную пластину, то для нее

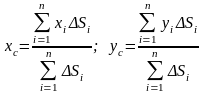
где 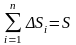- площадь всей пластины

Точку С, координаты которой определяются формулами называют центром тяжести площади S.

(Для однородной пластины центр тяжести пластины совпадает с центром тяжести площади; у неоднородной - не совпадает)

Суммы произведений вида

называются статическими моментами площади относительно соответствующих осей x и y.

Статическим моментом площади относительно оси, лежащей в плоскости сечения, называется сумма произведений из элементарных площадок на расстояния от центра тяжести этих площадок до оси.

Размерность статического момента площади – [м³]

Точно так же получаются формулы для координат центра

тяжести линии.

Здесь

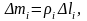
где - линейная плотность;

- длина элемента линии.

Тогда ,

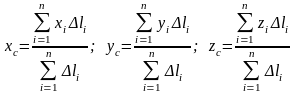где 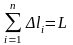- длина всей линии.

По этим формулам находят центры тяжести изделий из тонкой проволоки постоянного сечения.

Таким образом, центр тяжести однородного тела определяется как центр тяжести соответствующего объема, площади или линии.

3. Способы определения координат центра тяжести

При определении координат центров тяжести можно указать конкретные методы.

1. Симметрия

а) Если однородное твердое тело имеет плоскость геометрической симметрии, то центр тяжести этого тела находится в этой плоскости симметрии.

б) Если однородное твердое тело имеет ось геометрической симметрии, то центр тяжести находится на этой оси.

в) Если однородное твердое тело имеет центр геометрической симметрии, то центр тяжести совпадает с этим центром.

Из свойств симметрии следует, что центр тяжести однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре (центре симметрии) этих тел.

2. Метод разбиения тела на части.

Если тело модно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно определить непосредственно по вышеуказанным формулам. При этом число слагаемых в каждой из сумм будет равно числу частей, на которые разбито тело.

3. Метод отрицательных масс

Предположим, что твердое тело имеет пустые полости, то есть, полости в которых нет массы. Пусть, например, пустая полость имеет объем V_II ; координаты ее центра тяжести С₂ (x₂,, y₂, z₂) и радиус-вектор .

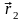Центр тяжести тела, фактически дополненного материей (без V_II) обозначим С₁, а объем этого тела V_I .

Используя метод разбиения на части , выразим радиус-вектор центра тяжести всего V , в таком виде

где 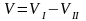- объем тела с пустой полостью.

Для координат центра тяжести соответственно имеем

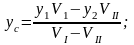
Из изложенного следует, что при вычислении координат центра тяжести тела, имеющего пустоты, в формулах статические моменты каждой пустоты ставятся со знаком «минус».

4. Метод интегрирования

Если тело нельзя разбить на несколько конечных частей, положение центров тяжести которых известны, то тело разбивают сначала на произвольные малые объемы , для которых формулы принимают вид:

и т.д.

где x_i, y_i, z_i – координаты некоторой точки, лежащей внутри объема .

Затем в равенствах (4.5) переходят к пределу при стремлении к нулю.

Тогда

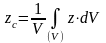
5. Экспериментальные методы

Центры тяжести неоднородных тел сложной конфигурации (самолет, паровоз и т.п.) можно определить экспериментально. Один из возможных экспериментальных методов – метод подвешивания – состоит в том, что тело подвешивают на нити или тросе за различные его точки, Направления нити, на которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела.

Другим возможным способом экспериментального определения центра тяжести является метод взвешивания.