2. Центр тяжести твердого тела.

Пусть точки А₁, А₂,…, A_n приложения параллельных сил являются фиксированными, то есть, не переносятся вдоль их линии действия. На линии действия равнодействующей имеется одна определенная фиксированная точка , вокруг которой поворачивается равнодействующая сила при повороте всех сил вокруг параллельных осей или просто их точек приложения на одинаковый угол в одну и ту же сторону.

Эту точку называют центром системы параллельных сил.

Центром системы , ,…, , параллельных сил называют точку, через которую проходит линия действия равнодействующей силы системы как угодно направленных параллельных сил.

Найдем координаты центра системы параллельных сил. Пусть имеем систему параллельных сил , ,…, , точки приложения которых А₁, А₂,…, A_n . Радиусы-векторы этих точек относительно начала координат системы Oxyz обозначим 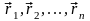. Точка С – центр этой системы, 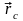- радиус-вектор точки С.

Введем единичный вектор 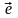, параллельный силам системы. Тогда

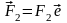= , ,…, и , где , ,…, и R – алгебраические значения параллельных сил.

По теореме Вариньона или

Заменяем векторы сил их выражениями через единичный вектор .

Тогда = или переместив скалярные множители в векторных произведениях, получим

=

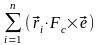
Перенеся все члены этого равенства в одну сторону, и вынося за скобку вектор , получим

=0

Вектор 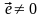. Следовательно, равна нулю разность в скобках, то есть,

Из этого равенства получим формулу, определяющую радиус-вектор точки С (центра параллельных сил):

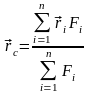
Проецируя обе части этого равенства на оси координат, получаем формулы для координат центра системы параллельных сил:

; ;

Суммы 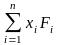; ; 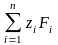называют статическими моментами системы параллельных сил относительно плоскостей yoz, zox и xoy.

Из формулы получаем, например,

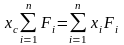
или, учитывая

то есть, статический момент системы параллельных сил относительно какой-либо плоскости равен статическому моменту равнодействующей силы относительно той же плоскости, если за точку ее приложения принять центр системы параллельных сил.

На все тела, расположенные в области притяжения Земли, действует сила притяжения. Если тело разбить на отдельные элементарные частицы малых объемов, то на каждую малую частицу будет действовать сила земного притяжения. При изучении многих явлений, происходящих под действием силы притяжения Земли, можно считать, что Земля представляет собой однородный шар. Тогда земное притяжение, действующее на любую материальную точку, выразится силой, приложенной к этой материальной точке и направленной к центру Земли.

Для тел, размеры которых очень малы, по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела.

Поле сил тяжести, в котором выполняются эти два условия, называют однородным полем тяжести.

Равнодействующую сил тяжести действующую на частицы данного тела, обозначим . Модуль этой силы называется весом тела и определяется равенством

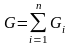
При любом повороте тела силы 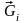остаются приложенными в одних и тех же точках тела и параллельными друг другу, изменяется только их направление по отношению к телу. Следовательно, равнодействующая сил будет при любых положениях тела проходить через одну и ту же неизменно связанную с телом точку С, являющуюся центром параллельных сил тяжести Эта точка и называется центром тяжести.

Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве. Координаты центра тяжести, как центра параллельных сил, определяются по формулам:

,

где x_i , y_i , z_{i -} координаты точек приложения сил тяжести , действующих на частицы тела.

Центр тяжести (т. С) – это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).

Координаты центров тяжести тел, объемов, плоских фигур и линий.