3. Равновесие с учетом силы трения

Изучение равновесия тел с учетом трения сводится к рассмотрению предельного положения равновесия, когда сила трения достигает максимальной величины . Поскольку реальная реакция связи шероховатой поверхности имеет две составляющие , то при изменении силы трения от нуля до максимальной, реакция меняется от 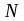до предельной величины , а угол ее отклонения от нормали будет изменяться от нуля до предельного :

÷ ÷ ÷ .

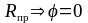Наибольший угол , который реакция образует с нормалью к поверхности, называют углом трения:

Статический коэффициент трения равен тангенсу угла трения. Если 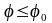, то тело находится в равновесии.

Рис. 3

Круговой конус с вершиной в точке О и с образующими, составляющими угол с нормалью, называют конусом трения (Рис. 3). До тех пор, пока реакция связи будет находиться внутри конуса трения, тело будет оставаться неподвижным.

Тема 3. Центр тяжести лекция № 5 центр тяжести

1. Центр параллельных сил

2. Центр тяжести твердого тела

3. Способы определения координат центра тяжести

Литература: Парфенов Ю.М., Теплов Г.Д., Цыглин В.А. Механика, ч.1, СПБВМИ, 2006,

стр. 70 – 84.

1. Центр параллельных сил.

Понятие о центре параллельных сил используется при решении некоторых задач механики, в частности при определении положений центров тяжести тел.

Рассмотрим способ сложения параллельных сил системы и определения положения центра приложения равнодействующей этих сил. Начнем с двух параллельных сил.

Пусть к твердому телу в точках А₁ и А₂ приложены две параллельные силы и , направленные в одну сторону (Рис. 1) . Эта плоская система сил имеет равнодействующую = + 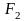, линия действия которой параллельна слагаемым силам и проходит через некоторую точку С, лежащую на прямой А₁А₂ . Положение точки с можно найти с помощью теоремы Вариньона.

Рис. 1

Согласно этой теореме

или

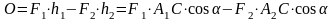
откуда 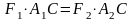или

где 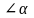- угол между прямой А₁ А₂ и перпендикуляром к линии действия сил.

Из выражения следует, что точка приложения равнодействующей С, расположенная на отрезке А₁А₂ , делит этот отрезок на части, обратно пропорциональные силам.

В равенство входят модули сил F₁ и F₂ .

Если силы и повернуть около точек приложения их А₁ и А₂ в одну и ту же сторону на один и тот же угол, то образуются две новые параллельные силы и , имеющие те же модули F₁ и F₂. Следовательно для сил и , равенство сохраняется и линия действия их равнодействующей то же пройдет через точку С. Такая точка называется центром параллельных сил и .

Очевидно, для всякой системы параллельных сил, приводящейся к равнодействующей силе , при повороте всех сил вокруг параллельных осей на один и тот же угол, равнодействующая поворачивается на тот же угол.

Сложение системы параллельных сил.

Пусть дана система параллельных сил , ,…, , приложенных к точкам А₁, А₂,…, A_n

твердого тела, причем эти силы, как сонаправлены, так и противоположно направлены (Рис. 2).

Рис. 2

Для сложения сил данной системы сил используем способ последовательного сложения:

- сложим последовательно силы системы одного направления и найдем их равнодействующую ;

- затем сложим последовательно силы системы противоположного направления и также найдем их равнодействующую .

В результате сложения всех сил системы получим две силы и - параллельные и

противоположно направленные. Их равнодействующая равна алгебраической разности и направлена в сторону большей силы. При этом могут быть три случая:

- система параллельных сил имеет равнодействующую, то есть приводится к равнодействующей (общий случай);

- система параллельных сил приводится к паре сил ( , ) и не имеет равнодействующей;

-силы и уравновешиваются, то есть, система параллельных сил является уравновешивающейся ( , ,…, ,)  0.

В дальнейшем при сложении системы параллельных сил будем рассматривать только общий случай, когда система параллельных сил эквивалентна равнодействующей .