
- •Вариант 1
- •Вариант 2
- •А. Исследовать и решить систему уравнений:
- •Найти собственные значения и собственные векторы матрицы:
- •Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 31
- •Вариант 32
- •Вариант 33
- •Вариант 34
- •Вариант 35
- •Вариант 36
- •Вариант 37
- •Вариант 38
- •Вариант 39
- •Вариант 40
Вариант 1
а. Исследовать и решить систему уравнений:

б. Найти
фундаментальную систему решений:

с. Решить
матричное уравнение:

Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
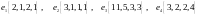 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
 в этом базисе.
в этом базисе.а. Найти ортогональную проекцию вектора
 на подпространство, натянутого на
векторы:
на подпространство, натянутого на
векторы:
 .
.
б. Найти матрицу линейного
преобразования (в базисе, в котором
заданы координаты всех векторов),
переводящего векторы
 в векторы
в векторы
 соответственно:
соответственно:

V. Найти угол между
вектором
 и подпространством, натянутым на векторы
и подпространством, натянутым на векторы
 ,
,
 ,
,
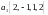 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
 к каноническому виду и написать этот
канонический вид.
к каноническому виду и написать этот
канонический вид.
2. Определить форму, размеры и расположение поверхностей заданных уравнениями:

Вариант 2
А. Исследовать и решить систему уравнений:
б. Найти
фундаментальную систему решений:

с. Решить
матричное уравнение:

Найти собственные значения и собственные векторы матрицы:
Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
а. Ортогонализовать и дополнить до ортонормированного базис
 ,
,
 ,
,
 .
.
б. Найти матрицу линейного
преобразования, переводящего векторы
 ,
,
 ,
,
 соответственно в векторы
соответственно в векторы
 ,
,
 ,
,
 .
.
Найти угол между вектором
 и подпространством, натянутым на векторы
и подпространством, натянутым на векторы
 и
и
 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
 к каноническому виду. Выписать
канонический вид формы.
к каноническому виду. Выписать
канонический вид формы.
2. Определить вид, размеры и расположение поверхностей заданных уравнениями:

Вариант 3
а. Исследовать и решить систему уравнений:

б. Найти
фундаментальную систему решений:

с. Решить
матричное уравнение:

Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
 в этом базисе.
в этом базисе.а. Ортогонализовать и дополнить до ортонормированного базис
 ,
,
 ,
,
 .
.
б. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы в векторы соответственно:

Найти угол между вектором
 и подпространством, натянутым на векторы
и подпространством, натянутым на векторы
 и
и
 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
 к каноническому виду. Выписать
канонический вид формы.
к каноническому виду. Выписать
канонический вид формы.
2. Определить вид, размеры и расположение поверхностей заданных уравнениями:

Вариант 4
а. Исследовать и решить систему уравнений:

б. Найти
фундаментальную систему решений:

с. Решить
матричное уравнение:

Найти собственные значения и собственные векторы матрицы:

Показать, что векторы
 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
 в этом базисе.
в этом базисе.а. Ортогонализовать и дополнить до ортогонального базис
 ,
,
 ,
,
 .
.
б. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы в векторы соответственно:

Найти угол между вектором и подпространством, натянутым на векторы
 и
и
 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
 к каноническому виду. Выписать
канонический вид формы.
к каноническому виду. Выписать
канонический вид формы.
2. Определить вид, размеры и расположение поверхностей заданных уравнениями:

