Задача 6.

Х

Дано:

S ₀ = 400 м

S₁= 61,0 м

S₂ = 13,6 м

_β⁰ = 30”

S₂ = 1/2000

m_β -?

β

С′

С

m_у

m_х

М

У

Рис. 4 Визначення положення точки

способом полярних координат

Розв’язання.

Положення точки С, яке виражене через полярну відстань S і кут β, характеризується координатами: х = S cos β ,у = S sin β.

Середня квадратична похибка зміщення точки С відносно проектного зображення:

М² = m²_х + m²_у,

де: m_х, m_у, - середні квадратичні похибки зміщення точки С по осям відповідно Х та У.

Їх знаходять як функцію полярного кута β і відстані S:

де: m_s .m_β – середні квадратичні похибки відкладення на місцевості полярної відстані S і кута β.

Тоді:

М² =

Застосовуючи принцип однакового впливу на точність розпланування споруди лінійних і кутових вимірювань.

Обчислюють значення похибки лінійних і кутових вимірювань:

M_s = M/ =2 / = 1,4мм

m _β = М / 2S = 206265 х 0,02 / 2 х61 =33,8′′

Отже, потрібна точність розпланування споруди може бути забезпечена застосуванням сталевої рулетки і теодоліта точністю 30′′.

З адача 7.

Д ано:

D = 78,32м

γ₁ = 19⁰ 50′

γ

γ₁

₂ = -1⁰43′

m

H

γ₂

_γ = 15′′

m_s = ± 0,02м

m _н - ?

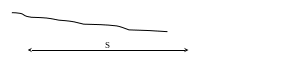
Рис. 5 Визначення висоти споруди

тригонометричним нівелюванням.

Розв’язання.

Висоту споруди обчислюють за формулою тригонометричного нівелювання,

H = S х ( tg γ_{1 +} tg γ₂),

де: tg γ_1,+ tg γ₂ – тангенси кутів нахилу;

Н = 88,46х ( tg14⁰ 42′ + tg1⁰65′) = 26,42м

Середня квадратична похибка значення висоти як функція виміряних величин:

m_n = ,

де: = tg γ_1,+ tg γ₂ = 0,28;

Звідси:

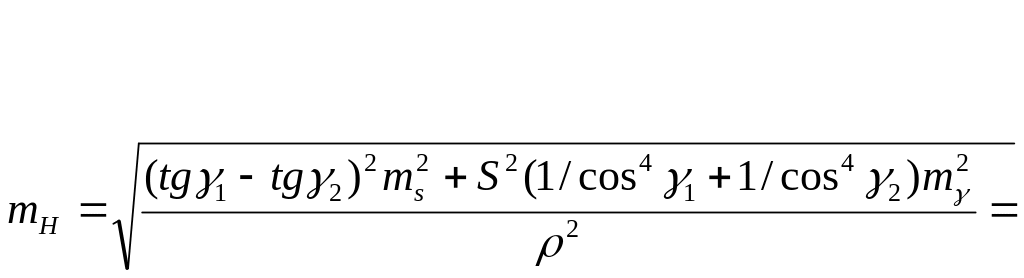
= =  м

Отже, середня квадратична похибка визначе ння висоти споруди тригонометричного нівелювання:

m_H = ± м

Зм.

Лист

№ докум.

Підп.

Дата