Арк.
РГР
00000018
Д
ано:
L
Lпр.
Lз = 113,68 м
∆
Р1
Р2
Lзвор..
Рис.1 Вимірювання
сторони теодолітного ходу в
прямому і зворотному напрямках.
∆′ - ? Lсер. - ?
Розв’язування.
Різниця результатів вимірювання:
∆ = Lп - Lз = 113,66 – 113,68 = -0,02 м.
Середнє арифметичне з результатів двох вимірювань:
Lсер. = 0,5 х (Lп + Lз) = 0,5 х (113,66+113,68) = 113,67 м.
Відносна похибка вимірювання довжини сторони теодолітного ходу в прямому і зворотному напрямках:
∆′ = ∆/ Lсер. = -0,02/113,67 = -1/5683<1/3000
Оскільки ∆′ = ∆доп., за остаточну довжину сторони теодолітного ходу приймають середнє арифметичне за результатами двох вимірювань: Lсер. =113,67м.
Задача 2
Дано:
С
Д
β
А
В
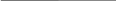
β2 = 64001′
β3 = 64002′
β4 = 63059′
β5 = 64001′
β
β
Р1
Р2
mсер. - ? ∆сер. - ?
Рис. 2 Вимірювання кута теодолітом
Розв’язування.
Розрахунки виконуються в табличній формі. Похибка одного вимірювання кута теодолітом:
∆1 = β1 - х = 630 58′ - 640 00 ′ = -02′ ∆2 = β2 - х = 640 01′ - 410 00′ = +01′
∆3 = β3 - х = 640 02′ - 640 00′ = +02′ ∆4 = β4 - х = 630 59′ - 410 00′ = -01′
∆5 = β5 - х = 640 01′ - 640 00′ = +01′ ∆6 = β6 - х = 630 59′ - 410 00′ = -01′
Визначення середньої і середньоквадратичної похибок одного вимірювання.
-
Номер вимірювання
Результати вимірювання, βі
Дійсна похибка
∆і
∆і2
Оцінка точності
1
63059′
-02
4
∆сер. = -4/6 = 0,66′
m =
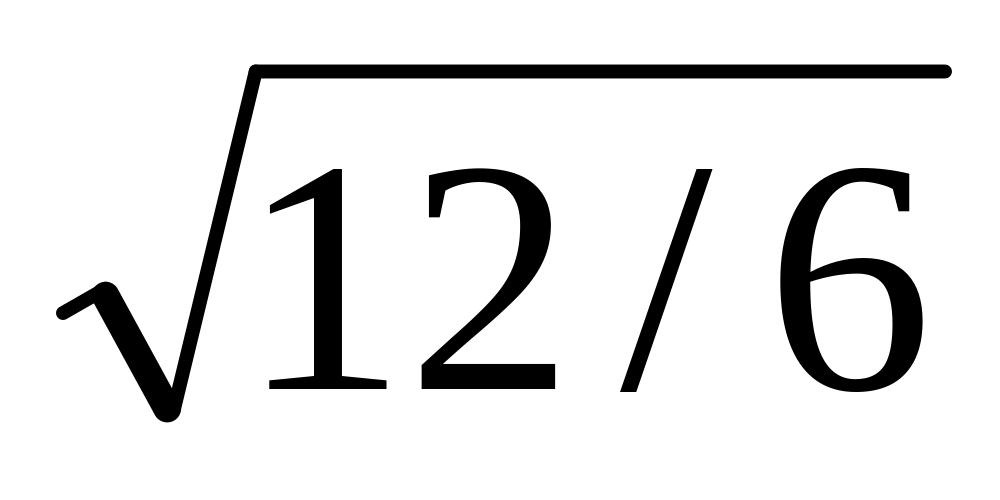= 1,68′2
64002′
+01
1
3
64058′
-02
4
4
63058′
-01
1
5
64002′
+01
1
6
63058′
-01
1
n = 6
Х = 64000′
(∆) = -4
(∆2) = 12
Середня похибка одного вимірювання:
∆сер. = (|∆1| + | ∆2 | + | ∆3 |+ | ∆4 | + | ∆5 | + | ∆6 |) / 6,= 8:6 = 1,33′
де: |∆1| , | ∆2 |,…. абсолютні дійсні похибки окремих вимірювань. Середньоквадратична похибка одного вимірювання:
m
=
=
=1,68′
Задача 3.
Д
ано:
L1 = 439,934м L4 = 439,941м
L2 = 439,948м L5 = 439,935м
L3 = 439,949м L6 = 439,938м
P = 0,9973
n = 6
x
- ? m
- ? М - ?
- ?
Розв’язування.
Обчислення проводять в табличній формі. Найімовірніше значення сторони полігонометрії:
Х = [L] / n = (L1 + L2 + L3 + L4 + L5 + L6) / 6 = 439,940
де: [L] – сума результатів вимірювань довжини сторони;
n – кількість вимірювань
Визначення найімовірнішого значення довжини сторони,
ймовірних похибок окремих вимірювань і середньоквадратичної похибки одного вимірювання.
-
Номер вимірювання
Вимірювання довжини сторони, м
Остача
Еп, мм
Ймовірна похибка
Vп, мм
Vп2
Оцінка точності
1
439,934
34
-5
25
Х = 439,95
м = ± 5,9 мм
М = ± 14,4 мм
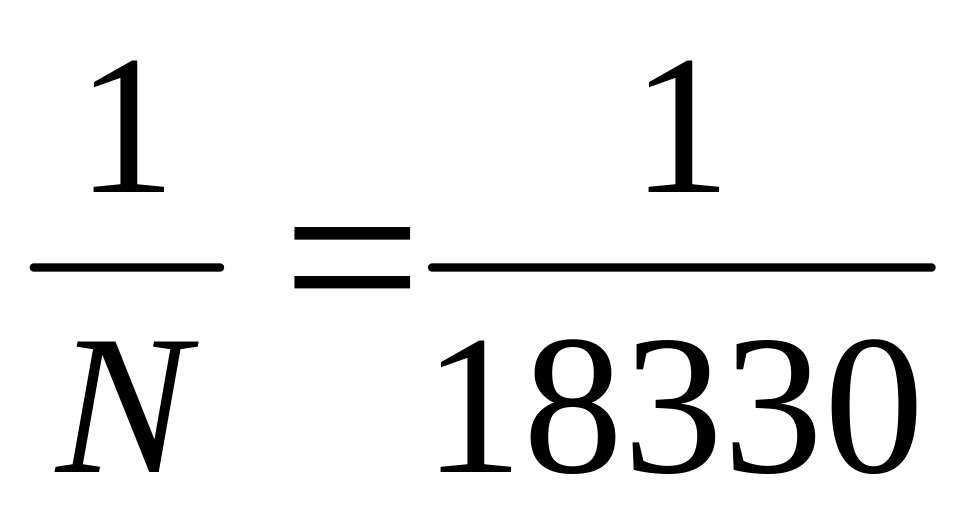
2
439,948
48
+7
49
3
439,949
49
+9
81
4
439,941
41
+0,9
0,81
5
439,935
35
-4
16
6
439,938
38
-2
4
Lсер. = 439,9
[Е] = 245
[V] = +5.9
175,8
Похибки окремих вимірювань: Vі = Lі – х; = 439,934 – 439,94 = - 0,005 (5)
Середньоквадратична похибка одного вимірювання:
m
=
=
±5,9
мм
де: [ V] – сума квадратів найімовірніших похибок окремих вимірювань.
Середня квадратична похибка арифметичної середини:
М
= m
/
=
± 2,4
мм
Відносна похибка найімовірнішої довжини сторони полігонометрії:
1/N = М / х = 1/18330
L = L0 = ( Е1 + Е2 + Е3 + … + Е ) /п = 439,9+ 0,245/6= 439,94
Межова похибка середньоарифметичного значення довжини сторони полігонометрії з довірчою ймовірністю:
∆0 = М t = 14,5 х 5,50 = 79,2 мм
де: М – середньоарифметична похибка арифметичної середини;
t – число, залежне від прийнятої довірчої ймовірності і кількості додаткових вимірювань N = (n – 1) = 5 (згідно з таблицею t = 4,04).
Отже , дійсне значення довжини сторони полігонометрії знаходять з інтервалу:
(Х- ∆0)≤ L ≤(Х+ ∆0),
тобто:
439,900 – 0,079≤ L ≤ 439,900 + 0,079
або:
439,821≤ L ≤ 439,979