1. Свободные механические колебания. Колебания- процесс повторяющийся во времени. Если время каждого колебания одинаково: ПЕРИОД КОЛЕБАНИЯ.(это время одного колебания. В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают свободные колебания. Свободными колебаниями называются колебания, которые происходят в системе, предоставленной самой себе, после выведения ее каким-либо способом из положения равновесия.

Собственными называются свободные колебания, возникающие в колебательной системе в отсутствие сил сопротивления (трения).

Колебания в подобной системе описываются уравнением вида

,

а сама система называется гармоническим осциллятором. Это дифференциальное уравнение свободных колебаний. Где х-координата, а амега0-циклическая частота собственных колебаний. Решение уравнения: x(t) A соs (_ot + ) , где А- амплитуда колебаний А=х max, Ф- фаза колебаний скобки. фи-начальная фаза (т=0).

2. Математический и пружинный маятники. Математический маятник

Это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити.

Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает. Далее процесс повторяется. Период колебаний математического маятника зависит от его длины, определяется по формуле

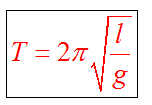
т- период колебания мат-го маятника, l-длина нити маяка, ускорение свободного падения джи.

Пружинный маятник

Это груз, прикрепленный к пружине, массой которой можно пренебречь.

Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости.

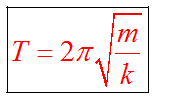
м-масса маятника, к- жесткость пружины.

3. Сложение гармонических колебаний одного направления и одинаковой частоты. Векторные диаграммы колебаний: 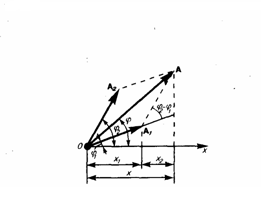векторы A₁ и A₂ вращаются с одинаковой угловой скоростью ω₀, то разность фаз (φ₂ - φ₁) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет 

 амплитуда А и начальная фаза φ соответственно определяются выражениями      

Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз  в зависимости от разности фаз (φ₂ - φ₁):  1) φ₂ - φ₁ = ±2mπ (m = 0, 1, 2, ...), тогда A=A₁+A₂, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;  2) φ₂ - φ₁ = ±(2m+1)π (m = 0, 1, 2, ...), тогда A=|A₁–A₂|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.  Когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями. 

(φ₂ - φ₁) складываемых колебаний.

4. Свободные электрические колебания. При электромагнитных колебаниях в колебательной системе происходят периодические изменения физических величин, связанных с изменениями электрического и магнитного полей . Простейшей колебательной системой такого типа является колебательный контур, то есть цепь, содержащая индуктивность и емкость.

Рассмотрим электрическую цепь, состоящую из катушки индуктивностью L и конденсатора электроемкостью C. Если предварительно зарядить конденсатор , то получим колебательный контур

 В начальный момент времени конденсатор имеет максимальный заряд, обладает максимальной энергией W_C.  В следующий момент времени конденсатор начинает разряжаться. В цепи появляется ток. По мере разрядки конденсатора ток в цепи и в катушке нарастает. Из-за явления самоиндукции это происходит не мгновенно. Энергия катушки W_L становится максимальной.  Электрические заряды вновь накапливаются на конденсаторе, но обкладка конденсатора, первоначально заряженная положительно, будет заряжена отрицательно. Энергия конденсатора максимальная.

 Конденсатор разряжается, но ток протекает уже в обратном направлении.

Этот процесс будет повторяться снова и снова. Возникнут электромагнитные колебания. Если отсутствуют потери (R=0), то сила тока, заряд и напряжение со временем изменяются по гармоническому закону.

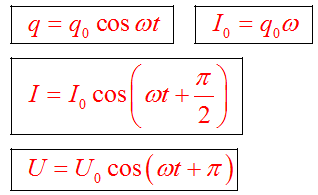
Период колебаний. Формула Томсона

Наименьший промежуток времени, в течение которого происходит переход зарядов с одной обкладки конденсатора на другую и обратно, называется периодом свободных электромагнитных колебаний.

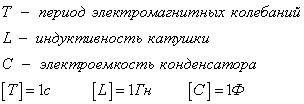
Энергия колебательного контура

Если пренебречь потерями (R=0), то полная энергия колебательного контура остается постоянной. Выполняется закон сохранения энергии.

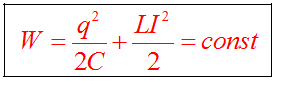
5. Затухающие колебания.

Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления. где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ  или и обозначим:

где   представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

в случае малого сопротивления среды   , решением уравнения будет Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину   обычно называют периодом затухающих колебаний коэффициент затухания есть физическая величина, обратная промежутку времени τ, в течение которого амплитуда убывает в е раз. Величина τ называется временем релаксации.

6. Переменный эл. Ток. Закон Ома для цепи переменного тока.

Переменный ток-это ток, сила или направление которого (или то и другое в месте) изменяются во времени. Закон Ома- физический закон определяющий зависимость между электрическими величинами напряжением, сопротивлением и током для проводников. I=U/R, но только если цепь состоит из одних активных сопротивлений к которым относятся эл. проводники. Если в цепи есть спирали с большим количеством витков или спирали надетые на железные сердечники то формула: Z=(2+X2)в степени 1/2 . Активное сопротивление на индуктивное сопротивление = общее сопротивление. и тогда закон Ома: I=U/Z .

7. Интерференция света.

Интерференцией называется явление перераспределения энергии в пространстве при наложении когерентных волн.

Когерентными называются волны одного направления, с одинаковыми плоскостями колебаний светового вектора, одинаковой частотой и с постоянной во времени разностью фаз.

Когерентные волны можно получить, разделяя одну световую волну на две с помощью отражения и преломления света.

Условия наблюдения максимумов и минимумов интерференции определяются разностью фаз складываемых колебаний.

Разность фаз интерферирующих волн связана с оптической разностью хода

  l₂ – l₁ ,

где l – оптическая дина пути световой волны. При этом l = Sn, где S – геометрическая длина пути световой волны в однородной среде с показателем преломления n. Кроме того, при нахождении l надо учитывать, что при отражении от оптически более плотной среды световая волна меняет фазу на . В этом случае к оптической длине пути надо прибавить (или отнять) ₀/2.

Связь разности фаз с оптической разностью хода дает общие условия наблюдения интерференционных максимумов и минимумов.

8. Методы наблюдения интерференции. Интерференцией называется явление перераспределения энергии в пространстве при наложении когерентных волн.

Когерентными называются волны одного направления, с одинаковыми плоскостями колебаний светового вектора, одинаковой частотой и с постоянной во времени разностью фаз.

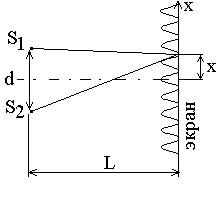
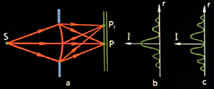
1. Интерференция наблюдается на экране, расположенном параллельно двум когерентным источникам в виде щелей (опыт Юнга, зеркала Френеля, бипризма Френеля) (Рис. 6).

L – расстояние от экрана до источников, отстоящих друг от друга на расстоянии d (d << L);

x – расстояние от центра интерференционной картины до k-ой интерференционной полосы.

Тогда

2. Интерференция при отражении от тонких пленок. При падении света на тонкую пленку происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные волны 1 и 2, которые могут интерферировать (рис. 7). При этом

,

где d – толщина пленки, n – показатель преломления,  – угол падения, ₀/2 – добавочная разность хода, учитывающая смену фазы на  при отражении 1-й волны от более плотной среды (пленки).

d

n



1

2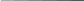

3. Кольца Ньютона – пример полос равной толщины, наблюдаемых при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 8).

Тогда радиусы темных колец Ньютона в отраженном свете , (50) а радиусы светлых колец Ньютона в отраженном свете

. (51)

Здесь R – радиус кривизны линзы, n – показатель преломления вещества между линзой и пластинкой.

r

R

n

9. Интерференция света в тонких пленках. . Интерференция при отражении от тонких пленок. При падении света на тонкую пленку происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные волны 1 и 2, которые могут интерферировать (рис. 7). При этом

,

где d – толщина пленки, n – показатель преломления,  – угол падения, ₀/2 – добавочная разность хода, учитывающая смену фазы на  при отражении 1-й волны от более плотной среды (пленки).

d

n



1

2

10. Кольца Ньютона

Кольца Ньютона – пример полос равной толщины, наблюдаемых при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 8).

Тогда радиусы темных колец Ньютона в отраженном свете , (50) а радиусы светлых колец Ньютона в отраженном свете

. (51)

Здесь R – радиус кривизны линзы, n – показатель преломления вещества между линзой и пластинкой.

r

R

n

11. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракцией называется огибание волной препятствий. Дифракция выражена достаточно сильно, если длина волны соизмерима с размерами препятствия. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса: каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент. Для количественной оценки результатов дифракции и нахождения амплитуды результирующей волны в любой точке пространства Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. дифракции Френель предложил разбивать фронт волны не на бесконечное множество точечных источников, а на конечное число зон. Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на /2. длина волны света/2. объясняет прямолинейность распространения света в свободной от препятствий однородной среде.

Колебания, приходящие в точку наблюдения P от аналогичных точек двух соседних зон, будут находиться в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на .

Радиус внешней границы k-ой зоны Френеля в этом случае

где а – расстояние от источника света до фронта волны, b – расстояние от точки наблюдения до вершины фронта волны О.

Для плоской волны радиус находится как .

12, Дифракция Френеля на круглом отверстии и диске. Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на /2. длина волны света/2. Для качественной оценки результата дифракции на малом круглом отверстии достаточно найти количество зон Френеля, попавших в это отверстие. Если количество зон четное, то в точке Р будет минимум, если нечетное – максимум.

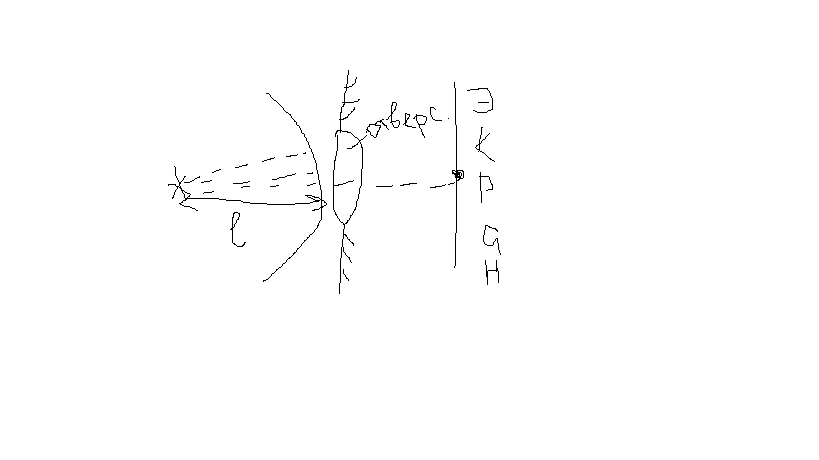
d- отверстие

l=d в квадрате/лямбду(длину волны света) l- расстояние от источника до отверстия.

на круглом отверстии и

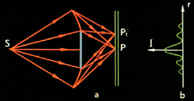
на круглом диске.

Если открыто ровно m первых зон Френеля, то амплитуда в точке P равна A=A₁-A₂+...±A_m.

Если m нечетное число, то эта формула преобразуется в следующую A=A₁/2+A_m/2, и в точке P поле усиливается, интенсивность I имеет максимум (b). r- расстояние на экране, отложенное от точки P.



=dsin

P

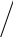
Если m четное число, то A=A₁/2-A_m/2 , и в точке P получается темное пятно

Если закрыть m первых зон Френеля, то амплитуда в точке P будет равна

A=A_m+1-A_m+2-...=A_m+1/2+(A_m+1/2-A_m+2+A_m+3/2)+...=A_m+1/2.

Таким образом, в центре геометрической тени, в точке P  будет светлое пятно

14. Дифракция Фраунгофера на дифракционной решетке. Большое практическое значение имеет дифракция Фраунгофера на так называемой дифракционной решетке. Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей

Расстояние d между серединами соседних щелей называется постоянной или периодом решетки. При этом в направлениях, для которых разность хода волн от соседних щелей равна целому числу длин волн, будут наблюдаться максимумы интенсивности, называемые главными. Таким образом, условие главных максимумов имеет вид

dsin = 2k/2, k = 0, 1, 2...

При этом интенсивность главных максимумов I_max пропорциональна интенсивности I_ , создаваемой в направлении  одной щелью. I_max = N²I ,

где N – общее число щелей решетки.

Дифракционная решетка служит спектральным прибором, разрешающая способность которого

где  – наименьшая разность длин волн двух близких спектральных линий с длинами волн  и +, при которых они еще воспринимаются раздельно (разрешаются).

Разрешающая способность дифракционной решетки может быть найдена по формуле

R=kN,

где k – порядок дифракционного спектра, N – общее число щелей решетки.

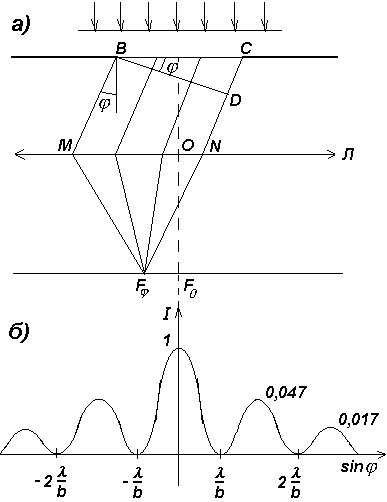
13. Дифракция Фраунгофера на одной щели. параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель ВС, имеющая постоянную ширину b и длину l>>b  Оптическая разность хода между крайними лучами ВМ и CN, идущими от щели под углом  к оптической оси линзы OF₀ =CD=bsin.Разобьем щель ВСна зоны Френеля, имеющие вид полос, параллельных ребру Вщели. Ширина каждой зоны выбирается (согласно методу зон Френеля) так, чтобы разность хода от кПри интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.Всего на ширине щели уместится D:

l/2= bsinj/(l/2) зон. Если число зон четное, т.е.

bsinj/(l / 2)=± 2mили bsinj=± ml , m=1,2,3-, 

то наблюдается дифракционный минимум (темная полоса).Если число зон нечетное, т.е.

bsinj/(l / 2)= ± (2m+1)или bsinj= ± (2m+1)  , m=1,2,3-, 

то наблюдается дифракционный максимум (светлая полоса).

раев этих зон была равна l/2.Углы, под которыми наблюдаются максимумы всех порядков, начиная с первого, зависят от длины волны света . Поэтому, если щель освещать немонохроматическим светом, то максимумы, соответствующие разным длинам волн, будут наблюдаться под разными углами и, следовательно, будут пространственно разделены на экране. Получим дифракционный спектр, в отличие от призматического спектра