МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

Лекція 10

Тема: " Транспортні мережі та потоки "

Дисципліна : "Дискретная математик"

Викладач Гусарова І. Г.

Харків 2014

1.Транспортні мережі та потоки. Постановка задачі

Нехай  орієнтований граф без петель, у якого кожній дузі приписане ціле ненегативне число  його пропускна здатність.

Визначення. Граф називається транспортною мережею (або, коротше, мережею), якщо

1) існує одна й тільки одна вершина (вхід), у яку не заходить жодна дуга;

2) існує одна й тільки одна вершина (вихід), з якої не виходить жодна дуга (мал. 4.44).

Рис. 4.44

Визначення. Вершини, відмінні від входу й виходу , називаються проміжними.

Позначимо через і множина всіх дуг графа , що заходять у вершину й, відповідно, що виходять із неї. Якщо  функція, задана на дугах графа ,  якеабо множина дуг, то через позначимо суму значень функції по всіх дугах множини :

.

Визначення. Функція , визначена на дугах мережі й приймаюча цілочисельні значення, називається потоком на цій мережі, якщо для кожної проміжної вершини

. (4.4)

і для кожної дуги

. (4.5)

Визначення. Дуга називається насиченої потоком , якщо ; вільної, якщо .

Замість того, щоб сказати, що на мережі заданий потік, часто говорять: через мережу пропущений потік. Будь-яка дуга входить (і притім точно по одному разі) у множини . З рівності (4.4) слідує:

.

Число називається величиною потоку . Одна з основних задач теорії мереж полягає в знаходженні максимального потоку по даній мережі.

Задачі такого типу часто зустрічаються при плануванні поставок, перевезень, різного роду розподілів; ряд інших задач безпосередньо зводиться до неї. Задачу про максимальний потік доводиться вирішувати й при додаткових умовах: ураховувати вартість перевезень, необхідний час, кількість транспортних одиниць, які на те або інший час можна залишити в проміжних пунктах і т.д.

2. Алгоритм знаходження максимального потоку

Пропустимо через мережу який-небудь початковий потік : наприклад, для будь-якої дуги . Описаний нижче алгоритм дозволить нам збільшити потік, або покаже, що наявний потік максимальний.

Пронумеруємо в довільному порядку проміжні вершини, позначаючи їх . Позначимо вхід знаком 0. Якщо  яка-небудь із уже позначених вершин, то позначимо її знаком всі вершини, у які заходять ненасичені дуги, що виходять із вершини (зокрема, +0 всі вершини, у які можна потрапити із входу по ненасиченій дузі). Знаком позначимо всі ті вершини , у які можна повернутися з позначеної вершини по невільній дузі в напрямку, протилежному її орієнтації. Інакше кажучи, вершину позначаємо знайомий , якщо існує невільна дуга, що виходить із і заходить у вже позначену вершину . Деякі вершини мережі при цьому можуть виявитися не позначеними, інші  позначеними кілька разів. У випадку, коли вихід не позначений, буде показано, що потік максимальний.

Допустимо, що вихід позначений (очевидно, знаком «+», тому що з нього не виходить жодна дуга). Відновимо порядок, у якому нам удалося позначити вихід, тобто з'єднаємо вхід з виходом ланцюгом (саме ланцюгом, а не шляхом), що проходить по позначених вершинах від вершини до вершини, позначеної або . Підкреслимо, що всі вершини ланцюга різні й позначені номерами попередніх вершин (і знаком «+» або «»).

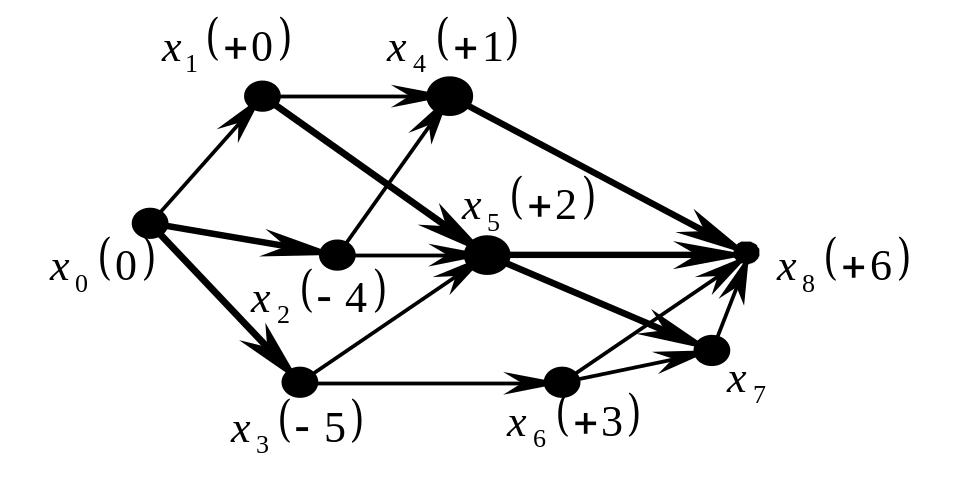
Рис. 4.45

На мал. 4.45 зображена мережа, насичені дуги якої показані жирними стрілками. По інших дугах іде потік, відмінний від нуля. При цьому умові вихід можна позначити (позначки вершин розставлені на мал. 4.45). Ланцюг позначених вершин має вигляд:

.

Частково порядок вершин у ній протилежний орієнтації дуг.

Визначимо наступну функцію на множині дуг мережі: , якщо дуга не належить до виділеного нами ланцюга ; , якщо й при русі по ланцюгу від входу до виходу дугу проходять у напрямку її орієнтації: якщо й при русі по ланцюгу від входу до виходу дугу проходять у напрямку, протилежному її орієнтації . Побудована в такий спосіб знову є потоком, нехай  довільна проміжна вершина. Якщо не належить ланцюгу, то , . Ці ж рівності справедливі й для вершини , що належить ланцюга , якщо вона є початком (або, відповідно, кінцем) двох дуг ланцюга (див. мал. 4.46).

Рис. 4.46 Рис. 4.47

Якщо ж точка належить ланцюгу , будучи початком однієї з дуг цього ланцюга й кінцем для іншої (див мал. 4.47), то або , , або , . У всіх випадках .

Крім того, якщо дуга належить ланцюгу і її напрямок збігається з напрямком руху по від входу до виходу, то вона ненасичена: . По визначенню . Якщо дуга належить ланцюгу і її напрямок протилежній напрямку руху по від входу до виходу, то вона невільна, . Тоді . У той же час величина потоку зросла на одиницю: . Незначна зміна цього алгоритму дає можливість прискорити процедуру, одержуючи більший приріст потоку.