5 Конвекция и диффузия (6 часов).

Лекция 10. Установившаяся одномерная конвекция и диффузия. Постановка задачи. Дискретный аналог. Существующие схемы решения. Схема против потока. Точное решение. Общая формулировка дискретного аналога. Методика и результаты применения различных разностных схем.

Лекция 11. Дискретный аналог для двух- и трех- мерных задач. Односторонняя пространственная координата. Условия на выходной границе. Схемная искусственная диффузия. Оценка неточности решения. Пористая стенка.

Лекция 12. Разностные схемы в STAR-CD. Методология использования разностных схем высшего порядка. Схема дискретизации первого порядка - дискретизации против потока. Схемы дискретизации по пространству высокого порядка: LUD, CD, QUICK, MARS, SFCD, Gamma, схема со смешанными разностями. Методология использования схем высокого порядка в STAR-CD.

Установившаяся одномерная конвекция и диффузия 5-1

Постановка задачи 5-1

Дискретный аналог 5-1

Существующие схемы решения 5-2

Схема против потока 5-3

Точное решение 5-3

Общая формулировка дискретного аналога 5-5

Методика и результаты применения различных разностных схем 5-6

Дискретный аналог для многомерных задач 5-7

Получение двухмерного дискретного аналога 5-7

Дискретный аналог для трехмерных задач 5-9

Односторонняя пространственная координата 5-9

Односторонние и двухсторонние координаты 5-9

Односторонний характер пространственной координаты 5-9

Условия на выходной границе потока 5-10

Схемная искусственная диффузия 5-11

Общий взгляд на искусственную диффузию 5-11

Анализ искусственной диффузии 5-12

Оценка точности по методу Рунге-Кутта 5-15

Пористая стенка 5-15

Схемы дискретизации первого порядка 5-16

Схема дискретизации против потока (UD) 5-16

Схемы дискретизации по пространству высокого порядка 5-16

Схема с линейной интерполяцией против потока (LUD) 5-17

Схема с центральным вычислением разностей (CD) 5-17

Схема вверх по потоку с квадратичной интерполяцией конвективной

кинематики (QUICK) 5-17

Монотоно адвективная (туманная) и перестраиваемая схема (MARS) 5-17

Самокорректирующаяся схема с центральными разностями (SFCD) 5-18

Схема Gamma - дискретизации (GAMMA) 5-18

Схема со смешанными разностями (BD) 5-19

Методология использования схем высокого порядка в STAR-CD 5-19

Установившаяся одномерная конвекция и диффузия Постановка задачи

Рассмотрим установившуюся одномерную задачу, в которой присутствуют только конвекция и диффузия. Дифференциальное уравнение сохранения имеет вид

, (5.1)

где u – скорость в направлении оси х. Для этого случая уравнение неразрывности записывается следующим образом

или .

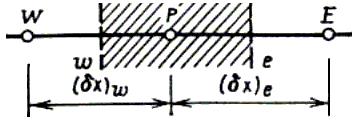
Рис. 5.1 Типичный шаблон узловых точек для одномерной задачи (заштрихованная область - КО)

Для получения дискретного аналога используем 3-точечный шаблон, показанный на рис. 5.1. Хотя действительное расположение граней контрольного объема e и w не должно влиять на окончательную форму записи, предположим, что грань e расположена посередине между узловыми точками P и E, а грань w - посередине между W и P.

Интегрируя уравнения (5.1) по КО, показанному на рис. 5.1, получаем

. (5.2)