Қос интегралдың анықтамасы.

Қос интегралдар екі айнымалы функция үшін анықталған интегралдың жалпыламасы болып табылады.

G – тұйық шектелген облыс, ал – G облысында анықталған және шектелген кез келген функция.

G облысының шекарасы және теңдеулерімен берілген қисықтардың ақырлы санынан тұрады деп ұйғарайық, мұндағы және – үзіліссіз функциялар.

G облысын аудандармен ортақ ішкі нүктелері жоқ n G_i бөлікке бөлейік (1-сурет). Әрбір G_i бөлікке кез келген нүктесін таңдап алып, G облысындағы функциясы үшін интегралдық қосынды деп аталатын қосынды құрамыз:

(1)

Осы облыстың шекаралық нүктелерінің ең үлкен ара қашықтығы диаметр деп аталады. Дербес G_i облыстардың ең үлкен диаметрін арқылы белгілеп , мынадай анықтама берейік:

Анықтама. (1) интегралдық қосындының ақырлы шегі

функциясының G облысы бойынша қос интегралы деп аталады және келесі символдардың бірімен белгіленеді:

(2)

Бұл жағдайда функциясы G облысында интегралданатын функция, ал G – интегралдау облысы, x және y – интегралдау айнымалылары, (немесе dxdy) – аудан элементі деп аталады.

1-теорема. G облысында үзіліссіз функциясы осы облыста интегралданады.

Алайда қос интеграл тек үзіліссіз функциялар үшін бар болады деп ойлауға болмайды. Анықталған интегралдар үшін орындалатын жалпыланған теореманың бұл жерде де орны бар.

2-теорема. G облысында шектелген және немесе үзіліссіз функцияларының графиктері болып табылатын қисықтардың ақырлы санында жататын нүктелерден басқа оның барлық жерінде үзіліссіз функциясы осы облыста интегралданады.

Қос интегралдың қасиеттері.

Қос интегралдың негізгі қасиеттері анықталған интегралдың сәйкес қасиеттеріне әбден ұқсас.

1⁰. Егер k – тұрақты сан және функциясы G облысында интегралданын болса, онда функциясы да G облысында интегралданады

,

яғни, тұрақты көбейткішті интеграл белгісінің алдына шығаруға болады.

2⁰. Егер және функциялары G облысында интегралданатын болса, онда олардың алгебралық қосындысы да осы облыста интегралданады және

.

3⁰. Егер G облысы әрқайсысында функциясы интегралданатын, ортақ ішкі нүктелері жоқ G₁ және G₂ облыстарының бірігуі болса, онда G облысында да бұл функция интегралданады және

.

4⁰. (Орта мән туралы теорема). Егер функциясы G облысында интегралданатын болса, онда осы облыста

,

орындалатындай нүкте табылады, мұндағы S – G фигурасының ауданы.

Қос интегралдарды есептеу тәсілдері.

Қос интегралды қайталанбалы түрге келтіру.

1. Тік бұрышты облыс. Координата осьтеріне параллель жақтары бар тік төртбұрыш бойынша алынған қос интегралды қарастырайық.

3-теорема. функциясы үшін тіктөртбұрышында

қос интегралы бар болсын.

кесіндісіндегі әрбір х үшін мынадай анықталған интеграл бар болсын

.

Онда

(3)

интегралы бар және келесі теңдік орындалады

. (4)

(4) формуланың оң жағында тұрған өрнек қайталанбалы интеграл деп аталады.

1-ескерту. Егер 3-теоремада х пен у орындарын ауыстырса, онда теорема қайталанбалы интегралдың бар болуын тұжырымдайды

(5)

және мына теңдік те орындалады

(6)

(4) және (6) формулалары қос интегралды қайталанбалы түрге келтіреді. Онда, мысалы, (6)-да интегралдау алдымен у тұрақты деп саналып, х бойынша жүреді, яғни, екі анықталған интеграл кезегімен есептеледі.

1-мысал. есептеңіз, мұндағы .

Шешуі: (6) формула бойынша

.

2-мысал. есептеңіз, мұндағы .

Шешуі: (4) формула бойынша

.

2. Қисық сызықты облыс. Енді қисық сызықты G облысы үшін қос интегралды қарастырайық.

4-теорема. функциясы облысында анықталсын, мұндағы және - үзіліссіз функциялар, үшін . Келесі қос интеграл бар болсын

,

және кесіндісінен әрбір х үшін

анықталған интеграл бар болсын. Онда мына қайталанбалы интеграл бар болады

және келесі теңдік орындалады

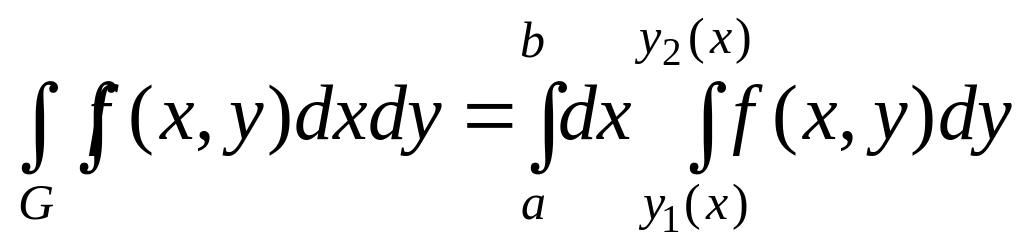. (7)

2-ескерту. Егер 4-теоремада х пен у орындарын ауыстырса, онда теорема қайталанбалы интегралдың бар болуын тұжырымдайды

және мына теңдік те орындалады

. (8)

3-мысал. есептеңіз, егер .

Шешуі: G – координата осьтерімен және түзуімен шектелген үшбұрыш.

Сондықтан, . (7) формула бойынша

.

Егер G облысында х және у орындарын ауыстырса, берілген интегралды (8) формула бойынша да есептеуге болады, Онда үшбұрыш мына теңсіздіктермен анықталады , осыдан , және

интегралы да сондай мәнге ие болатынын тексеру оңай.

4-мысал. қисықтарымен шектелген G облысы бойынша табыңыз (2-сурет).

Шешуі: Алдымен у, одан соң х бойынша интегралдап, мынаны аламыз:

;

Нәтижені интегралдау тәртібін өзгерту ақылы тексеруге болады.