2.4. Прямые и обратные задачи при начислении процентов и дисконтировании по простым ставкам

Как было показано выше, оба вида ставок (наращения и дисконтирования) применяются для решения сходных задач. Однако для ставки наращения прямой задачей является определение наращенной суммы, обратной – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении (табл. 2.2).

Очевидно, что рассмотренные два метода наращения и дисконтирования – по ставке наращения i и учетной ставки d – приводят к разным результатам даже тогда, когда i= d.

Таблица 2.2

Ставки	Прямая задача	Обратная задача
i	S = P (1 + ni)
d	P = S (1 – nd)

Учетная ставка отражает фактор времени более жестко. Влияние этого фактора усиливается при увеличении величины ставки.

Выбор конкретного вида процентной ставки заметно влияет на финансовые итоги операции.

2.4.1. Определение срока ссуды и величины процентной ставки. В тех случаях, когда известны величина долга в начале и в конце срока ссуды, а также процентная ставка, можно определить срок этой ссуды. Для простой ставки наращения срок ссуды определяется решением (2.3) относительно n:

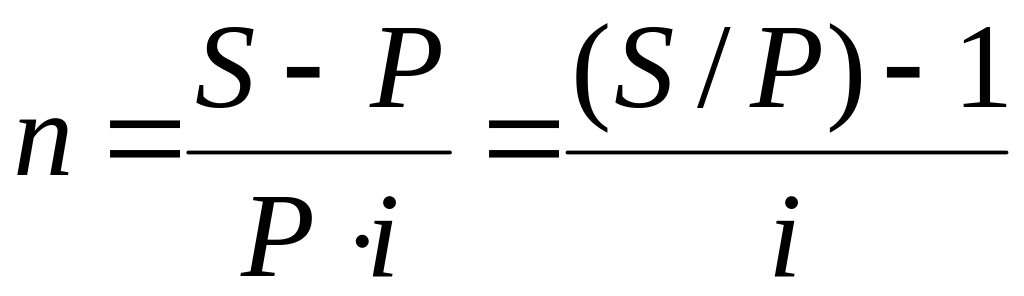. (2.15)

Для простой учетной ставки срок ссуды определяется решением (2.11) относительно n:

. (2.16)

Если необходимо определить срок в днях, то используют формулу (2.4).

Пример 2.9. Какова должна быть продолжительность ссуды в днях для того, чтобы долг, равный 9000 руб., вырос до 10000 руб. при условии, что простая ставка наращения равна 18,5% годовых при K=365?

Решение.

дней. 

В тех случаях, когда известны величина долга в начале и в конце срока ссуды, а также ее срок, можно определить процентную ставку этой ссуды. В этом случае процентную ставку называют доходностью ссудной операции. Для простой ставки наращения и простой учетной ставки срок ссуды определяется решением (2.3) и (2.11) относительно i и d соответственно:

; . (2.17)

Пример 2.10. В контракте предусматривается погашение обязательства в сумме 12000 руб. через 300 дней. Первоначальная сумма долга – 10000 руб. Определить доходность ссудной операции в виде простой годовой ставки наращения при K = 360.

Решение.

. 

Глава 3. Сложные проценты

В средне- и долгосрочных финансово-кредитных операциях, если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, применяют сложные проценты. База для начисления сложных процентов в отличие от простых не остается постоянной – она увеличивается с каждым шагом во времени. Таким образом, сложная процентная ставка наращения – это ставка, при которой база начисления является переменной, то есть проценты начисляются на проценты.

3.1. Формула наращения по сложным процентам

Формулу сложных процентов можно получить следующим образом. Предположим, что мы имеем P руб., которые можно инвестировать по процентной ставке наращения r. Через один период наращения (например, год) мы будем иметь P(1+r) руб. Если повторить этот процесс, инвестировав всю сумму P(1+r), то к концу второго периода будем иметь [P(1+r)](1+r) = P(1+r)². Продолжая процесс, видим, что показатель степени в формуле для наращенной суммы равен количеству периодов обращения. Приняв это число равным n, получим формулу сложных процентов.

S = P (1+ r)ⁿ, (3.1)

где S – наращенная сумма, P – первоначальный размер долга, r – сложная ставка наращения, n – срок задолженности (число периодов (лет) наращения), (1+r)ⁿ – множитель наращения по сложным процентам.

Пример 3.1. Какой величины достигнет долг, равный 1 млн. руб., через 5 лет при росте по сложной ставке 15,5% годовых?

Решение.

S = 1(1 + 0,155)⁵ = 2,055464 млн. руб. 

При наращении по сложным процентам наращенная сумма быстро растет при увеличении числа периодов (лет).

Формулу (3.1) используют и в том случае, когда срок для начисления процентов является дробным числом.

3.1.1. Переменные ставки. Формула (3.1) предполагает постоянную ставку на протяжении всего срока начисления процентов. В случае, когда изменения размеров ставок фиксируется в контракте, общий множитель наращения определяется как произведение частных, т.е.

S =  _... , (3.2)

где r₁, r₂, …, r_k – последовательные значения ставок;

n₁, n₂, …, n_k – периоды, в течение которых действуют соответствующие ставки.

Пример 3.2. Срок ссуды – 5 лет, договорная процентная ставка – 12% годовых плюс маржа 0,5% в первые два года и 0,75% в оставшиеся. Найти множитель наращения.

Решение.

м_н = (1+0,125)²(1+12,75)³ = 1,814. 

3.1.2. Начисление процентов при дробном числе лет. Часто срок в годах для начисления процентов не является целым числом. В некоторых коммерческих банках дробная часть долга отбрасывается и считается только целая часть. В большинстве случаев учитывается полный срок. При этом применяют два метода: 1) расчет по формуле (3.1); 2) смешанный метод, который предполагает начисление процентов за целое число лет по формуле сложных процентов и за дробную часть срока по формуле простых процентов:

S = P (1 + ai) (1+ r)^b, (3.3)

где a – дробная часть срока задолженности, b – целая часть срока задолженности, n = a + b – срок ссуды, i = r – при целой части сложный процент, при дробной – простой.

Пример 3.3. Кредит в размере 3 млн. выдан на 3 года и 160 дней под 16,5% годовых. Определить сумму долга на конец срока двумя способами, если K = 365*. Решение. 1) S = = 5,086593 млн. руб. 2) S = = 5,071932 млн. руб. * Если временная база не оговорена, то брать 360/360. 