Глава 8. Переменные ренты. Конверсия рент

В практике встречаются случаи, когда размеры членов потока платежей изменяются во времени. Такие изменения могут быть связаны с какими-либо обстоятельствами объективного порядка (например, условиями производства и сбыта продукции), а иногда и случайными факторами. Частным случаем такого потока является переменная рента. Переменной рентой называется поток платежей, у которого выплаты изменяются во времени по заданному закону (или условиям развития), а интервалы между выплатами постоянны.

Рассмотрим некоторые типы переменных рент.

8.1. Годовая рента постнумерандо с изменением выплат по закону арифметической прогрессии

Данный вид ренты еще называют рентой с постоянным абсолютным приростом платежей. Пусть выплаты изменяются по закону:

R, R+a; R+2a; R+3a; … R+(n – 1)a,

где R – выплата в конце первого года, a – постоянное годовое приращение выплат (темп роста платежей), n – срок ренты.

Определим современную стоимость такой ренты из суммы:

(8.1)

Умножим это равенство на (1 + r) и вычтем из обеих частей выражения соответствующие части равенства (8.1), после чего получим:

,

где – дисконтный множитель по ставке r;

– коэффициент приведения постоянной годовой ренты.

В итоге формулу для современной стоимости годовой ренты с изменениями платежей по закону арифметической прогрессии можно записать в виде:

(8.2)

Если известна современная стоимость годовой ренты, то её наращенная сумма может быть определена по формуле:

S = A(1 + r)ⁿ.

Подставив в эту формулу выражение для современной стоимости (8.2), получим:

(8.3)

Пример 8.1. Ожидается, что сбыт продукции будет увеличиваться каждый год на 2,5 тыс. руб. (или уменьшаться на 2,5 тыс. руб.) в течение 10 лет при поступлении денег в конце каждого года. Первая выплата равна 50 тыс. руб. Начисление процентов производится по ставке 12 % годовых. Определить современную стоимость и наращенную сумму переменного потока платежей.

Решение.

Современная стоимость исследуемого потока платежей определяется по формуле (8.2). Предварительно найдем коэффициент приведения постоянной ренты а_n;r:

.

Для а = 2,5 тыс. руб. современная стоимость потока платежей равна:

руб.

Для а = –2,5 тыс. руб. современная стоимость потока платежей равна:

руб.

Наращенная сумма исследуемого потока платежей определяется по формуле (8.3). Предварительно найдем коэффициент наращения постоянной ренты s_n;r:

.

Для а = 2,5 тыс. руб. наращенная сумма потока платежей равна:

руб.

Для а = –2,5 тыс. руб. наращенная сумма потока платежей равна:

руб. 

8.2. Годовая рента постнумерандо с изменением выплат

по закону геометрической прогрессии

Данный вид ренты еще называют рентой с постоянным относительным приростом платежей. Пусть выплаты изменяются по закону:

R, Rq; Rq²; … , Rq^n-1,

где R – выплата в конце первого года, q – темп роста ренты или знаменатель прогрессии, n – срок ренты.

Современная стоимость такой ренты определяется из суммы:

.

Если темп роста ренты представить в виде q = 1 + k, где k – темп прироста ренты, то формулу для современной стоимости годовой ренты с изменениями платежей по закону геометрической прогрессии можно записать в виде:

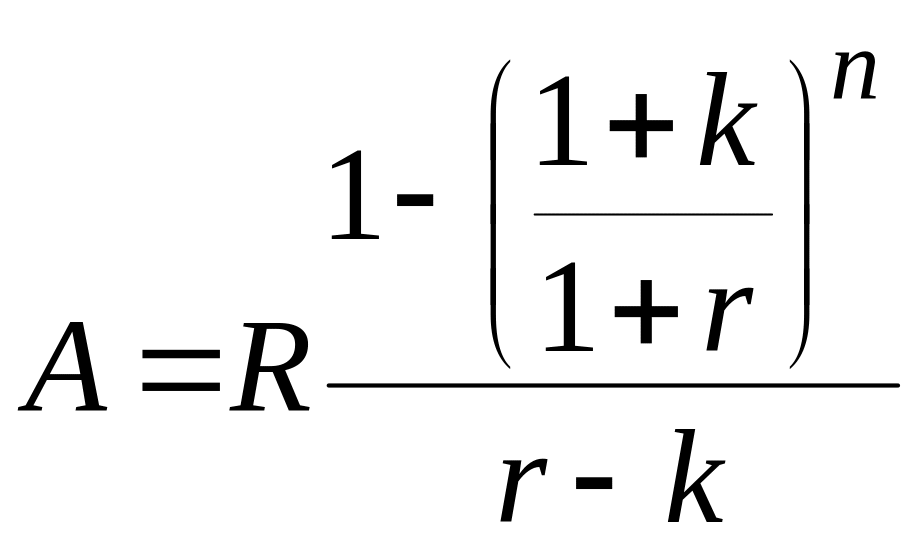. (8.4)

Заметим, что прирост может быть как положительным (k0), так и отрицательным (k0).

Наращенная сумма ренты находится как:

. (8.5)

Пример 8.2. Ожидается, что сбыт продукции будет увеличиваться каждый год на 5 % (или уменьшаться на 5 %) в течение 10 лет при поступлении денег в конце каждого года. Первая выплата равна 50 тыс. руб. Начисление процентов производится по ставке 12 % годовых. Определить современную стоимость и наращенную сумму переменного потока платежей.

Решение.

Современная стоимость исследуемого потока платежей определяется по формуле (8.4). Для k = 0,05 современная стоимость потока платежей равна:

руб.

Для k = –0,05 современная стоимость потока платежей равна:

руб.

Наращенная сумма исследуемого потока платежей определяется по формуле (8.5). Для k = 0,05 наращенная сумма потока платежей равна:

руб.

Для k = –0,05 наращенная сумма потока платежей равна:

руб. 

8.3. Конверсии рент

Виды конверсий. В практике иногда сталкиваются со случаями, когда на этапе разработки условий контракта или даже в ходе его выполнения необходимо в силу каких-либо причин изменить условия выплаты ренты. Иначе говоря, речь идет о конвертировании условий, предусматриваемых при выплате финансовой ренты. Основными видами конверсии являются:

1. замена ренты разовым платежом (выкуп ренты);

2. замена разового платежа рентой (рассрочка платежа);

3. объединение нескольких рент в одну (консолидация рент);

4. замена ренты с одними условиями на ренту с другими условиями.

Если предполагается, что конверсия не должна приводить к изменению финансовых последствий для каждой из участвующих сторон, то конверсия должна основываться на принципе финансовой эквивалентности (см. гл. 6).

Выкуп ренты. Данный вид конверсии сводится к замене ренты единовременным платежом. Искомый размер выкупа должен быть равен современной стоимости выкупаемой ренты. Для решения задачи выбирается та или иная формула расчета современной стоимости потока платежей (в зависимости от условий погашения задолженности). Применяемая при расчете современной стоимости процентная ставка должна удовлетворять обе участвующие стороны.

Рассрочка платежей. Если есть обязательство уплатить некоторую крупную сумму и стороны согласны, что задолженность будет погашена частями, т.е. в рассрочку, то ее удобнее осуществить в виде выплаты постоянной ренты.

Для решения задачи приравниваем современную стоимость ренты, с помощью которой производится рассрочка, сумме долга. Задача обычно заключается в определении одного из параметров этой ренты – члена ренты (платежа) или ее срока – при условии, что остальные параметры заданы. Такого рода задачи рассматривались в п. 7.4 (стр. 63), поэтому здесь нет смысла останавливаться на них.

Объединение (консолидация) рент. Объединение рент заключается, как правило, в замене нескольких рент одной. В этом случае из принципа финансовой эквивалентности следует равенство современных стоимостей заменяющей и заменяемых (консолидированных) рент, что соответствует равенству:

, (8.6)

где А – современная стоимость заменяющей ренты, А_q – современная стоимость q-й заменяемой ренты.

Объединяемые ренты могут быть любыми: немедленными и отсроченными, годовыми и p-срочными и т.д. Что касается заменяющей ренты, то следует определить ее вид и все параметры, кроме одного. Необходимо рассчитать размер неизвестного параметра исходя из равенства (8.6). Этим параметром является либо член ренты, либо ее срок.

Так, если задан срок заменяющей немедленной ренты постнумерандо n, то находится платеж заменяющей ренты из условия эквивалентности (8.6):

. (8.7)

В свою очередь, если задается сумма платежа (размер члена заменяющей ренты) и его периодичность, то находится новый срок ренты. Обычно задача сводится к расчету n по заданному значению коэффициента приведения а_n;r. Для немедленной ренты постнумерандо имеем:

. (8.8)

Если значение известно, то, определив на основе (8.8) величину n, получим:

. (8.9)

Пример 8.3. Три ренты постнумерандо – немедленные, годовые – заменяются одной отложенной на три года рентой постнумерандо. Согласно договоренности заменяющая рента имеет срок 10 лет, включая отсрочку. Характеристики заменяемых рент:

R_q = 100; 120; 300 тыс. руб., сроки этих рент: 6; 11 и 8 лет. Пересчет осуществляется по сложной ставке процентов 20% годовых. Определить заменяющий отложенный платеж.

Решение.

1) Определим сумму современных стоимостей заменяемых рент (табл. 8.1).

Таблица 8.1

Рента (q)	Rq, тыс. руб.	nq, лет	r, %		, тыс. руб.
1	100	6	20	3,32551	332,551
2	120	11	20	4,32706	519,247
3	300	8	20	3,83716	1151,148
Итого	520				2002,946

2) Зная сумму современных стоимостей заменяемых рент, определим размер заменяющего отложенного платежа:

R = 960,189 тыс. руб.

3) Если бы заменяющая рента была немедленной, без отсрочки, то платеж был бы равен:

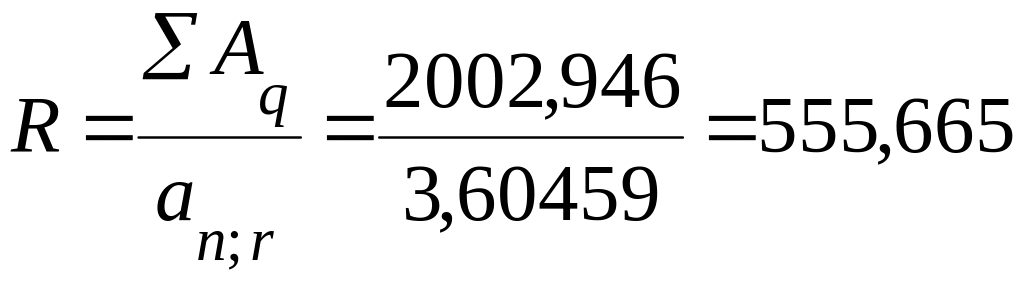тыс. руб.

Продолжим пример. Пусть теперь заданным является не срок, а сумма годового платежа, например, 1500 тыс. руб., и необходимо найти срок заменяющей ренты. В данном случае в начале определяется современная стоимость немедленной ренты, затем рассчитывается ее срок.

A = 2002,46  1,2³ = 3461,091 тыс. руб.

По формуле (8.9) получим:

года.

Округляем ответ до целого меньшего или целого большего (для кредитора – до меньшего n, заемщика – до большего n). В данном случае – 3 или 4 лет и компенсируем нехватку покрытия долга или излишки (см. пояснения в п. 7.4) при определении срока ренты. 

Пример 8.4. Три ренты заменяются одной р – срочной рентой с ежемесячными выплатами 3000 руб. в месяц. Параметры заменяемых рент:

1. годовая рента с ежегодными выплатами 10000 руб. в год в течение 7 лет, на которые начисляются проценты по ставке 15 % годовых;

2. годовая рента с ежегодными выплатами 10000 руб. в год в течение 7 лет, на которые начисляются проценты по номинальной ставке 15 % годовых, причем проценты начисляются поквартально;

3. рента с ежегодными поступлениями 10000 руб. в год в течение 7 лет, на которые начисляются проценты по ставке 15 % годовых, причем выплаты производятся поквартально, а проценты начисляются ежемесячно.

Пересчет осуществляется по процентной ставке 18 % годовых. Определить срок заменяющей ренты.

Решение. При составлении уравнения эквивалентности находят современную стоимость каждой из заменяемых рент, суммируют их и приравнивают эту сумму современной стоимости заменяющей р – срочной ренты, то есть:

= . (*)

1) Современная стоимость первой заменяемой ренты равна:

2) Современная стоимость второй заменяемой ренты равна:

3) Современная стоимость третьей заменяемой ренты равна:

4) Сумма современных стоимостей трех заменяемых рент равна:

=124800,73 руб.

5) Решая уравнение (*) относительно n, получим:

.

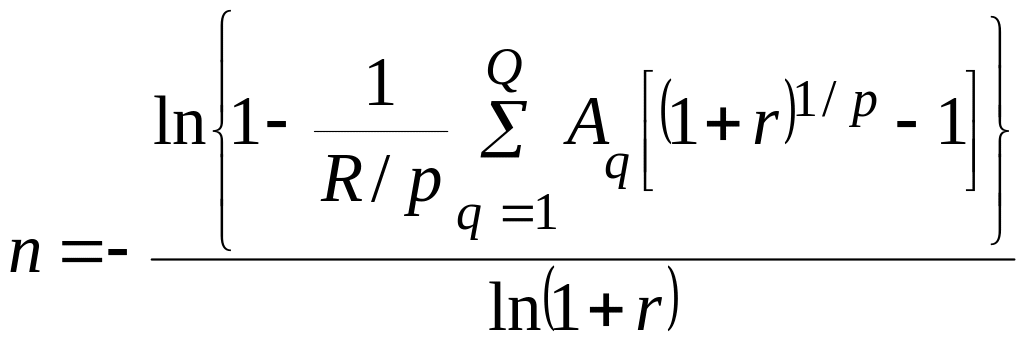Подставив сюда условия примера и сумму современных стоимостей трех заменяемых рент, найдем:

Округлим срок ренты до 5 лет и уточним величину ежемесячной выплаты. Ежегодная выплата заменяющей ренты определяется по формуле: .

Коэффициент приведения:

Ежегодная выплата:

Ежемесячная выплата: 