1.5. Построение планов ускорений
Рассмотрим построение плана ускорений для положения 2 (φ1=90º).
Положение 1, соответствующее холостому ходу.
Построение плана ускорений начинаем от входного звена ОА. Угловая скорость кривошипа ω1 = 70 рад/с.
Ускорение точки А определится как
aA = aAn + aAτ= ω12·ОА + ε1·ОА .
Так как ω1 = const, то ε1 = 0. Тогда
aA = aAn = ω12·ОА =702·0,15= 735,0 м/с2.
масштабный коэффициент плана находим как:
μа
= aA/
πa
= 735,0/100 = 7,35 м/с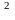
/мм
.
Из точки π , принятой за полюс плана, проводим вектор πa, направленный к центру вращения.
План ускорений для группы Ассура (2-3) строим, графически решая систему векторных уравнений
аB = аА + аnBA+ аτBA
аB= аC + аnВC + аτВC ,
В этой системе уравнений аА- ускорение точки А, аnBA- нормальное ускорение точки Bотносительно точки А, аτBA - тангенциальное ускорение точки Bотносительно точки. Поэтому
аτBA┴ АВ ;аτВC┴ ВС.
аnBA||АВ ; аnВC||ВС.
Найдем нормальные ускорения:
аnBA= ω22·АВ =3,22·0,65 = 6,66 м/с
аnВC= ω32·ВC = 15,542·0,65 = 157,0 м/с2 ,
Поделив полученные результаты на масштабный коэффициент, получаем длину векторов на плане ускорений.
nВA = аnBA/μа = 6,66/7,35 = 0,9 мм;
nВC = аnВC /μа = 157,0/7,35 = 21,4 мм;
Проводим все полученные векторы и получаем точку b.
Выходя из подобия получаем точку D:
dπ = DС·bπ/ВC = 0,23 ·36,9/0,65 =13,1 мм.
Чтобы построить план ускорений для группы Асура (4-5), решим систему уравнений:
aE = аD + аED
aE = вертикаль.
В этой системе уравнений aE – ускорение точки E, аED– относительное ускорение точки E относительно D, aD– ускорение точки D. Поэтому:
аED|| DE;
Проводим данные вектора в соответствующих положениях, находим точку е.
Рассчитываем полные ускорения точек центров масс звеньев (точки S5, S4), умножая длины соответствующих векторов πsiна масштабный коэффициент плана ускорений для положения 2 (φ1=90º).
aS2 = πs2·μа = 45,69·7.35 = 335,8м/с2 ;
aS3 = πs3·μа = 12,3·7.35= 90,4м/с2 ;
aS5 = πs5·μа = 10,5∙7,35 = 77,2м/с2 ;
Находим угловые ускорения звеньев:
ε2 = аτBA /AB = τAB·μа /AB = 119,9·7,35/0,65 = 13561/c2 .
ε3 = аτВC /BC = τВC·μа /BC= 30,1·7,35/0,65 = 340,41/c2 .
Для положения на холостом ходе построение плана ускорений аналогично.
Результаты расчетов сведены в таблицу 2.2.
Таблица 2.2 Линейные ускорения центров масс и угловые ускорения звеньев
-
Поло-
жение
φ1,
рад
Линейные ускорения, м/с2
Угловые ускорения, 1/с2
аS2
аS3
аS5
ε2
ε3
2
π/4
335,8
90,4
77,2
1356
340,4
7
7π/4
572,8
193
205,1
978,1
885,4
2. Силовой расчет рычажного механизма
2.1 Определение сил, действующих на звенья механизма.
Вычерчиваем на листе (см. лист 2) кинематическую схему механизма в положении 2 (φ1=90º). Переносим с листа 1 план ускорений механизма и определяем ускорения центров масс звеньев 2, 3 и 5 и угловое ускорение звеньев 2, 3 (см. п.1.4).
aS2 = πs2·μа = 45,69·7.35 = 335,8м/с2 ;
aS3 = πs3·μа = 12,3·7.35= 90,4м/с2 ;
aS5 = πs5·μа = 10,5∙7,35 = 77,2м/с2 ;
ε2 = аτBA /AB = τAB·μа /AB = 119,9·7,35 /0,65 = 13561/c2 .
ε3 = аτВC /BC = τВC·μа /BC= 30,1·7,35/0,65 = 340,41/c2 .
Рассчитываем величины сил инерции
Fи2= -m2·аs2 = 5· 335,8= 1679 Н,
Fи3= -m3·аs3 =6·90,4 = 542,4 Н,
Fи5= -m5·аs5 =8·77,2 = 617,6Н,
и моментов сил инерции
Mи2= -Js2·ε2 = 0,07·1356 = 94,92Нм
Mи3= -Js3·ε3 = 0,12·340,4 = 40,85Нм
Силы инерции прикладываются в центрах масс звеньев: в т. Е, S3, S2, в направлениях, противоположных векторам ускорений центров масс. Моменты сил инерции прикладываем к звеньям 2 и 3 в направлениях, противоположных угловым ускорениям, ε2 и ε3.
Сила производственного сопротивления постоянна на протяжении всего рабочего хода (по условию) и составляет Рпс= 450 Н.
Кроме силы производственных сопротивлений Рпс, сил инерции Fи3, Fи5 и моментов сил инерции Ми2, Mи3 на звенья механизма действуют силы тяжести G5, G3 , G2. Определяем силы тяжести
G2= -m2·g =5·9.81 = 49,0 Н,
G3= -m3·g = 6·9.81 = 58,9 Н,
G5= -m5·g = 8·9.81 = 78,5 Н,
Силы тяжести прикладываются в центрах масс звеньев вертикально вниз.
2.2 Замена сил инерции и моментов сил инерции
Для звена 3 заменяем момент сил инерции Ми3 на пару сил Fи3',и Fи3˝ равной по величине:
Fи3'=Fи3˝= Mи3/СB=40,85/0,65=62,9 Н
Для звена 2 заменяем момент сил инерции Ми2 на пару сил Fи2',и Fи2˝ равной по величине:
Fи2'=Fи2˝= Mи2/АВ=94,92/0,65=146,0 Н