1 Построение проверяющего и диагностических тестов для непрерывной

системы

1.1 Построение проверяющего теста для непрерывной системы

Системы железнодорожной автоматики, телемеханики и связи (СЖАТС) с непрерывными сигналами имеют те особенности, которые позволяют при их анализе отдать предпочтение логическим моделям. Применение логических моделей связано с допусковыми методами контроля, которые характеризуются тем, что заключение о техническом состоянии объекта составляют по результатам оценки значений сигналов в контрольных точках (значений контролируемых параметров объекта). Результаты контроля параметров при этом приводят к оценкам вида: « в норме – не в норме», т.е. к оценкам двузначного типа (1- единица или 0 - нуль). В этих случаях удобно применять логические модели и различные логические методы.

Логическая модель может быть построена для объекта диагноза, имеющего непрерывные сигналы, если он обладает следующими свойствами: объект можно разделить на несколько связанных между собой функциональных элементов; каждый функциональный элемент имеет два состояния - работоспособное и неработоспособное; для всех входных и выходных параметров всех элементов можно выделить области их допустимых и недопустимых значений; выходной параметр элемента является допустимым в том случае, если сам элемент работоспособен и все приложенные к нему входные воздействия допустимые.

В процессе построения логической модели можно выделить несколько этапов. На первом этапе построения модели систему разделяют на отдельные функциональные элементы, входы и выходы которых доступны для измерения. Выбор этих элементов определяется необходимой глубиной диагноза. На втором этапе построения модели составляют функциональную схему системы как объекта диагноза, в которой указывают все выделенные элементы и связи между ними. Затем для каждого элемента указывают значения допустимых входных и выходных воздействий.

Рассмотрим функциональную схему объекта диагноза, которая приведена на рисунке 1 . Эта схема содержит восемь элементов Э1 – Э8, имеет четыре внешних входных воздействия х₁– х₄ и формирует три выходные реакции у₆ - у₈ . Каждый элемент формирует свою выходную реакцию у_i , причем выходные реакции элементов Э6 –Э8 совпадают с выходными реакциями схемы. В том случае, если i –е входное воздействие или выходная реакция j – го элемента являются допустимыми, то примем, что х_i = 1 и у_i =1, в противном случае х_i = 0 и у_i = 0. Обозначим n – разрядным двоичным числом состояние системы, содержащей n элементов, в котором i – й разряд равен 1(0), если i – й элемент исправен (неисправен). В общем случае система, состоящая из n элементов, имеет 2ⁿ состояний, из которых одно исправное и 2^n-1 неисправных. В приводимом примере ограничимся рассмотрением только одиночных неисправностей

s₀ =11111111, s₁ =01111111, s₂ =10111111, s₃ =11011111, s₄ =11101111,

s₅ =11110111, s₆ =11111011, s₇ =11111101, , s₈ =11111110.

В случае использования логической модели предполагается, что на входы объекта диагноза поступает единственное входное воздействие, определяемое допустимыми значениями всех сигналов.

Следовательно, возможные элементарные проверки будут отличаться только наборами контрольных точек, в которых осуществляются измерения. При этом задача построения алгоритма диагноза сводится к выбору совокупности контрольных точек, достаточной для решения определенной задачи диагноза. Каждая проверка имеет 2^k исходов, где k – число контролируемых элементов. Общее число проверок 2ⁿ, где n- число элементов системы. На практике большое число проверок не может быть реализовано из-за отсутствия доступа к выходам некоторых элементов; невозможно подключиться сразу к выходам нескольких элементов и т.д.

В рассматриваемом примере будем считать, что возможны только те проверки, которые заключаются в измерении реакции на выходе одного элемента системы, причем для измерений доступны выходы всех элементов. Обозначим как π_i результат i – й элементарной проверки, т.е. контроль реакции на выходе i – го элемента (i {1,2, …,8}.

Таблица функций неисправностей (ТФН) для функциональной схемы объекта диагноза, которая представлена на рисунке 1, приведена в таблице 1

Таблица 1- Таблица функций неисправностей

Проверка	Результат Rij проверки для системы, находящейся в состоянии Si
	S0	S1	S2	S3	S4	S5	S6	S7	S8
Π1	1	0	1	1	1	1	1	1	1
Π2	1	0	0	0	0	0	0	0	1
Π3	1	0	1	0	1	1	1	1	1
Π4	1	0	0	0	0	0	0	0	1
Π5	1	0	0	0	0	0	0	0	1
Π6	1	0	0	0	0	0	0	0	1
Π7	1	0	0	0	0	0	0	0	1
Π8	1	0	0	0	0	0	0	0	0

В том случае, если система исправна (состояние S₀) и на всех входах присутствуют допустимые сигналы, то и на выходах всех элементов имеют место допустимые значения сигналов – 1. Отказ какого-либо элемента вызывает появление недопустимого значения сигнала на его выходе и на выходах всех связанных с ним элементов. Таблица функций неисправностей содержит всю необходимую информацию для построения, проверяющего и диагностического тестов. Каждый столбец ТФН задает некоторую функцию, определяемую на множестве проверок π_i

(i {1,2, …,8}). Функция равна единице, если проверка дает допустимый результат.

Примем следующие обозначения: F – функция исправного объекта; f_i – функция i - го состояния неисправного объекта или функция i - й неисправности.

Для рассматриваемого примера имеем:

F = π₁ π₂ π₃ π₄ π₅ π₆ π₇ π₈ ;

f₁ = 0; f₂ = π₁ π₃; f₃ = π₁; f₄ = π₁ π₃; f₅ = π₁ π₃; f₆ = π₁ π₃;

f₇ = π₁ π₃; f₈ = π₁ π₂ π₃ π₄ π₅ π₆ π₇;

При построении проверяющего теста Т_п для каждой неисправности вычисляют проверяющую функцию:

φ_i = F f_i . (1.1)

Проверяющая функция равна единице (φ_i = 1) только на тех проверках, на которых результаты проверок различны для исправной схемы и для схемы с i- й неисправностью, т.е. она объединяет те проверки, на которых i – я неисправность обнаруживается.

Проверяющий тест Т_п определяется по следующему выражению:

Т_п = φ₁ • φ₂ • ··· • φ_n , (1.2)

где n – число неисправностей.

Вычисляем проверяющие функции φ_i для рассматриваемого примера:

φ₁ = π₁ π₂ π₃ π₄ π₅ π₆ π₇ π₈ ;

φ₂ = π₂ π₄ π₅ π₆ π₇ π₈ ;

φ₃ = π₂ π₄ π₅ π₆ π₇ π₈ ;

φ₄ = π₂ π₄ π₅ π₆ π₇ π₈ ;

φ₅ = π₂ π₄ π₅ π₆ π₇ π₈ ;

φ₆ = π₂ π₄ π₅ π₆ π₇ π₈ ;

φ₇ = π₂ π₄ π₅ π₆ π₇ π₈ ;

φ₈ = π₈ ;

Записываем проверочный тест Т_п и производим его минимизацию:

Т_п = φ₁ • φ₂ • φ₃ • φ₄ • φ₅ • φ₆ • φ₇ • φ₈ = ( π₁ π₂ π₃ π₄ π₅ π₆ π₇

π₈ )(π₂ π₄ π₅ π₆ π₇ π₈)( π₂ π₄ π₅ π₆ π₇ π₈)( π₂ π₄ π₅ π₆ π₇ π₈)(π₂ π₄ π₅ π₆ π₇ π₈)(π₂ π₄ π₅ π₆ π₇ π₈)(π₂ π₄ π₅ π₆ π₇ π₈)(π₂ π₄ π₅ π₆ π₇ π₈) π₈ = π₈

Из полученного выражения, проверочного теста Т_п = π₈, следует, что для полной проверки системы, представленной функциональной схемой см. рисунок 1, необходимо и достаточно подать на внешние входы допустимые воздействия и измерить реакцию на выходе элемента Э8. Если система исправна, то на его выходе будет присутствовать допустимый сигнал, если же система неисправна, то на его выходе будет присутствовать недопустимый сигнал.

1.2 Построение диагностических тестов для непрерывной системы

Для решения задачи поиска неисправного элемента строят диагностический тест Т_д . Его определяют следующим образом.

Для каждой пары неисправностей (с номерами i и j) вычисляют различающую функцию:

φ_i,j = f_i f_j. (1.3)

Различающая функция равна единице (φ_i,j = 1) только на тех проверках, на которых результаты проверок различны для схем, находящихся в состоянии i и j неисправности ( каждая графа ТФН S_i с индексом i {1,2, …,8} соответствует определенной неисправности N_i).

Для всех различных пар неисправностей определяем различающие функции:

φ_1,2 = π₁ π₃ ; φ_1,3 = π₁; φ_1,4 = π₁ π₃ ; φ_1,5 = π₁ π₃ ; φ_1,6 = π₁ π₃ ; φ_1,7 = π₁ π₃ ; φ_1,8 = π₁ π₂ π₃ π₄ π₅ π₆ π₇ .

φ_2,3 = π₃ ; φ_2,4 = 0; φ_2,5 = 0; φ_2,6 = 0; φ_2,7 = 0; φ_2,8 = π₂ π₄ π₅ π₆ π₇ .

φ_3,4 = π₃ ; φ_3,5 = π₃ ; φ_3,6 = π₃ ; φ_3,7 = π₃ ; φ_3,8 = π₂ π₃ π₄ π₅ π₆ π₇ .

φ_4,5 = 0; φ_4,6 = 0; φ_4,7 = 0; φ_4,8 = π₂ π₄ π₅ π₆ π₇ .

φ_5,6 = 0; φ_5,7 = 0; φ_5,8 = π₂ π₄ π₅ π₆ π₇ .

φ_6,7 =0; φ_6,8 = π₂ π₄ π₅ π₆ π₇.

φ_7,8 = π₂ π₄ π₅ π₆ π₇.

В зависимости от решаемой задачи диагноза возможно использование одного из двух вариантов диагностического теста.

Первый вариант диагностического теста используют в том случае, если заведомо известно, что система неисправна, и поэтому перед тестированием ставится только одна задача – обнаружение неисправного элемента.

В этом случае тест Т_д вычисляют как логическое произведение различающих функций:

Т_д = φ_1,2 φ_1,3••• φ_n-1,n. (1.4)

Для рассматриваемого примера:

Т_д = φ_1,2 φ_1,3••••• φ_6,8 φ_7,8 = ( π₁ π₃) π₁ ( π₁ π₃)( π₁ π₃)( π₁ π₃) & & ( π₁ π₃)( π₁ π₂ π₃ π₄ π₅ π₆ π₇) π₃ (π₂ π₄ π₅ π₆ π₇ ) π₃& &π₃ π₃ π₃(π₂ π₃ π₄ π₅ π₆ π₇) (π₂ π₄ π₅ π₆ π₇ ) (π₂ π₄ π₅ π₆ π₇ ) (π₂ π₄ π₅ π₆ π₇ ) (π₂ π₄ π₅ π₆ π₇ ).

Минимизируем полученное выражение и получаем:

Т_д = π₁ π₃ (π₂ π₄ π₅ π₆ π₇ ).

Полученное выражение содержит пять минимальных тестов:

Т_д1 = π₁ π₂ π₃; Т_д2 = π₁ π₃ π₄; Т_д3 = π₁ π₃ π₅; Т_д4 = π₁ π₃ π₆; Т_д5 = π₁ π₃ π₇;

Рассмотрим тест Т_д2 = π₁ π₃ π₄ и построим для него словарь неисправностей.

Словарь неисправностей является частью ТФН. Его представляют в виде таблицы, строки которой соответствуют проверкам, содержащимся в Т_д2 , а графы соответствующим классам эквивалентных неисправностей. Словарь неисправностей для Т_д2 приведен в таблице 2.

Таблица 2 - Словарь неисправностей для диагностического теста Т_д2

Проверка	Результат Rij проверки для системы, находящейся в состоянии Si
	S1	S2 S4 S5 S6 S7	S3	S8
π1	0	1	1	1
π3	0	1	0	1
π4	0	0	0	1

Третья графа в таблице 2 соответствует классу эквивалентных неисправностей N₂ ,N₄ ,N₅ ,N₆ ,N₇ . В непрерывных системах такие классы образуют неисправности элементов, входящих в контуры, охваченные обратной связью. В функциональной схеме объекта диагноза (рисунок 1) такой контур образуют элементы Э2, Э4, Э5, Э6, Э7. При отказе любого элемента, входящего в контур, недопустимый сигнал появляется на выходах всех элементов контура.

Для определения отказавшего элемента в замкнутом контуре разрывают обратную связь.

Словарь неисправностей позволяет обнаруживать неисправный элемент при помощи формальной процедуры. Для этого на входы системы подают допустимые воздействия и производят измерения в контрольных точках, соответствующих проверкам, которые входят в словарь неисправностей. Результаты измерения сравнивают с данными, приведенными в словаре неисправностей. По совпадению судят о номере отказавшего элемента.

Второй вариант диагностического теста используют тогда, когда задача поиска неисправности и задача проверки исправности системы совмещаются в едином процессе диагноза. Такой подход часто используют на практике. В этом случае диагностический тест определяют по следующему выражению:

Т_д^* = Т_п φ_1,2 φ_1,3••• φ_n-1,n. (1.5)

Для рассматриваемого примера Т_д^* определяется как

Т_д^* = Т_п φ_1,2 φ_1,3••• φ_7,8 = π₈ ( π₁ π₃) π₁ ( π₁ π₃) ( π₁ π₃) ( π₁ π₃) ( π₁ π₃) ( π₁ π₂ π₃ π₄ π₅ π₆ π₇) π₃ (π₂ π₄ π₅ π₆ π₇ ) π₃& &π₃ π₃ π₃ (π₂ π₃ π₄ π₅ π₆ π₇) (π₂ π₄ π₅ π₆ π₇ ) (π₂ π₄ π₅ π₆ π₇ ) (π₂ π₄ π₅ π₆ π₇ ) (π₂ π₄ π₅ π₆ π₇ ).

После минимизации полученного выражения получаем

Т_д^* = π₁ π₃ π₈ (π₂ π₄ π₅ π₆ π₇ ).

Полученное выражение содержит пять минимальных тестов:

Т_д1^* = π₁ π₂ π₃ π₈ ; Т_д2^* = π₁ π₃ π₄ π₈ ; Т_д3^* = π₁ π₃ π₅ π₈ ; Т_д4^* = π₁ π₃ π₆ π₈ ;

Т_д5^* = π₁ π₃ π₇ π₈ ;

Тесты Т_д1^* ,Т_д2^* ,Т_д3^* ,Т_д4^* ,Т_д5^* обеспечивают полную проверку системы, а словари неисправностей содержат, помимо граф, соответствующим классам эквивалентных неисправностей, графу S₀ , соответствующую исправному состоянию системы.

В качестве примера приведем словарь неисправностей для теста Т_д2^* (см. таблицу 3).

Логические модели упрощают непрерывные объекты и поэтому не позволяют решать все задачи диагностики (в частности, не позволяют различать неисправности элементов, охваченных обратной связью). Поэтому их часто используют на первом этапе диагноза, так как они являются простыми и удобными для анализа. Для более полного анализа применяют другие методы.

Таблица 3- Словарь неисправностей для Т_д2^*

Проверка	Результат Rij проверки для системы, находящейся в состоянии Si
	S0	S1	S2 S4 S5 S6 S7	S3	S8
π1	1	0	1	1	1
π3	1	0	1	0	1
π4	1	0	0	0	1
π8	1	0	0	0	0

Варианты заданий для построения тестов непрерывных систем приведены в приложении А.

2. Построение тестов для объекта диагноза, реализованного на реле

0. Построение тестов для комбинационной релейно-контактной схемы

   0. Построение проверяющего теста для комбинационной релейно-контактной схемы

Релейно-контактные схемы (РКС) широко используются в устройствах железнодорожной автоматики, телемеханики и связи и состоят из контактов, обмоток реле и соединительных проводов. Контакты имеют два вида неисправностей: короткое замыкание – когда цепь остается замкнутой независимо от состояния реле; разрыв контакта – когда цепь остается разомкнутой независимо от состояния реле.

Обмотки реле также имеют два вида неисправностей (к ним относятся и неисправности механических элементов реле). При обрыве обмотки реле не включается, когда оно должно включатся. Причинами этого могут быть обрыв обмотки, межвитковые замыкания в ней, механические повреждения подвижных частей. При этом нормально замкнутые (тыловой и общий) контакты остаются замкнутыми, а нормально разомкнутые (общий и фронтовой) контакты - разомкнутыми. При ложном включении обмотки реле включается, когда оно не должно включатся. Причиной этого может быть соединение обмотки с источником питания, залипание или заклинивание якоря, сваривание замыкающих контактов. При этом размыкающие контакты размыкаются, а замыкающие – замыкаются.

Неисправность типа "обрыв обмотки" эквивалентна кратной неисправ­ности, в которую входят короткие замыкания всех размыкающих кон­тактов и разрыв всех замыкающих контактов, а неисп­равность "ложное включение обмотки" эквивалентна кратной неисправности, включающей в себя короткие замыкания всех замыка­ющих контактов и разрыв всех размыкающих контактов. Это об­стоятельство позволяет выявлять неисправности обмоток теми же способами, что и неисправности контактов, а в большинстве схем вообще рассматривать только неисправности контактов.

Поэтому элементарная проверка для релейно-контактной схемы заключается в подаче на ее входы определенного набора значений входных переменных (состояний кнопок SBA, SBB, SBC) и определении факта наличия проводимости схемы по состоянию реле F. Входные переменные обозначим строчными буквами, соответствующими обозначениям реле - а, b, с.

Рассмотрим построение проверяющего и диагностических тестов для релейно-контактной схемы, заданной в виде функции алгебры логики (ФАЛ) F={1,2,3,5}a,b,c.

Минимизируем заданную ФАЛ с помощью карты Карно и построим релейно-контактную схему для функции F={001,010,011,101}.

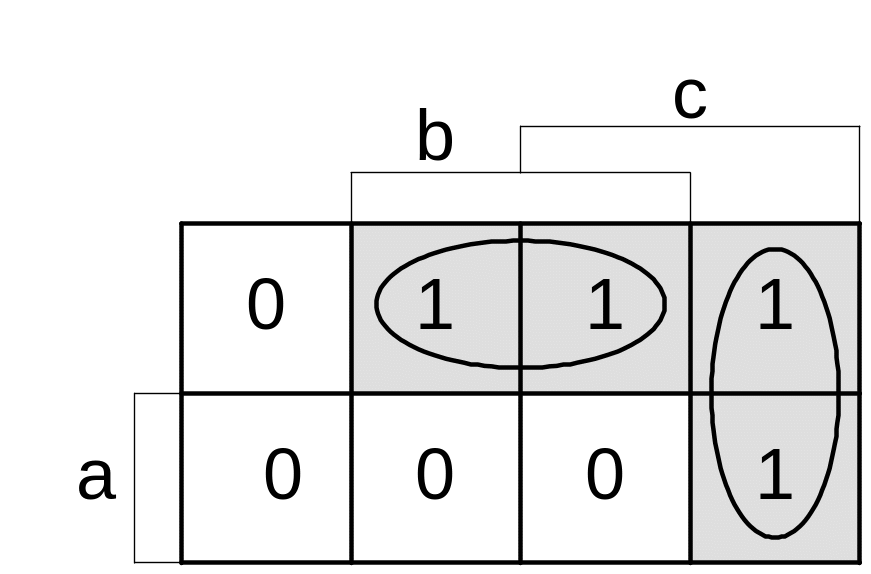
Рисунок 2 - Карта Карно функции F={001,010,011,101}

В результате получаем минимизированную функцию Комбинационная релейно-контактная схема, соответствующая полученной ФАЛ, представлена на рисунке 3. Она содержит три входных реле - А, В, С - и четыре контакта - a, b₁, b₂, с.

Общее число проверок для схемы с m входами равно 2^m. Рассмотрим только одиночные неисправности контактов. Для построения тестов релейно-контактной схемы будем использовать ТФН.

Рассматриваемая схема имеет восемь проверок, одно исправное и 8 неисправных состояний.

Функции неисправностей могут быть рассчитаны двумя методами. При первом методе неисправность вносят в схему и по полученной структуре схемы определяют искомую функцию. Схема с внесенной неисправностью – коротким замыканием контакта a реализует функцию ₁ = b₁ b₂ c. Второй метод использует влияние неисправности на формулу, отражающую структуру схемы.

Рисунок 3- Комбинационная релейно-контактная схема

Между ее буквами и контактами схемы существует взаимно однозначное соответствие. Короткое замыкание контакта соответствует переводу соответствующей буквы в единицу, а разрыв контакта - в нуль. Для короткого замыкания контакта a функция будет иметь вид ₁ = b₁ b₂ c. Для обрыва контакта a функция - ₂ = b₂ c.

В соответствии с рассмотренными методами определения функции неисправностей для множества неисправностей контактов схемы они имеют вид:

Для заданной релейно-контактной схемы ТФН представлена в таблице 4.

На основании построенной ТФН и в соответствии с выражением для вычисления проверяющей функции (1.1) находим проверяющие функции.

Таблица 4- Таблица функций неисправностей

Входной набор		F	f1	f2	f3	f4	f5	f6	f7	f8
			при внесении неисправности
№	a b c
0	0 0 0	0	0	0	1	0	1	0	0	0
1	0 0 1	1	1	1	1	1	1	0	1	0
2	0 1 0	1	1	0	1	0	1	1	1	1
3	0 1 1	1	1	0	1	0	1	1	1	1
4	1 0 0	0	0	0	0	0	1	0	0	0
5	1 0 1	1	1	1	1	1	1	0	1	0
6	1 1 0	0	1	0	0	0	0	0	0	0
7	1 1 1	0	1	0	0	0	0	0	1	0

Проверяющий тест в соответствии с выражением (1.2) равен

Т_п= φ₁ ·φ₂·φ₃·φ₄·φ₅·φ₆·φ₇·φ₈ = (6  7)· (2  3) · 0 ·(2  3) · (0  4)·(1  5) · 7· (1  5) =

= (2  3)· 0· (1  5) · 7 =0127  0257  0137  0357;

Это выражение содержит 4 минимальных теста.

Т_п1=0·1·2·7; Т_п2=0·2·5·7; Т_п3=0·1·3·7; Т_п4=0·3·5·7.

0. Построение диагностических тестов для комбинационной

релейно-контактной схемы

Для построения диагностических тестов, согласно выражению (1.3), для каждой пары неисправностей ТФН находим различающую функцию.

φ_1,2 = 2  3  6  7; φ_2,3 = 0  2  3; φ_3,4 = 0  2  3;

φ_1,3 = 0  6  7; φ_2,5 = 0  2  3  4; φ_{3, 5} = 4;

φ_1,5 = 0  4  6  7; φ_2,6 = 1  2  3  5; φ_3,6 = 0  1  5;

φ_1,6 = 1  5  6  7; φ_2,7 = 2  3  7; φ_3,7 = 0  7; φ_1,7 = 6;

φ _5,6=0  1  4  5;φ_5,7=0  4  7; φ_6,7= 1  5  7; φ_7,8= 1  5  7;

Диагностический тест первого вида определяем согласно выражению (1.4), при этом предполагается, что диагностируемая схема неисправна.

Диагностический тест для рассматриваемого примера имеет вид

Т_д = φ_1,2·φ_1,3··φ_6,7·φ_7,8 = 4·6·(0  2  3)(1  2  3  5)(2  3  7)(0  1  5)(1  5  7).

После выполнения процедуры минимизации полученного выражения и рассмотрения всего множества диагностических тестов получим, что оно содержит два минимальных теста: Т_д1 =2·4·5·6; Т_д2 =1·2·4·6.

Словарь неисправностей, построенный для Т_д1, представлен в таблице 5.

Поиск неисправности в заданной схеме осуществляют следующим образом. На входы схемы последовательно подают входные наборы, входящие в диагностический тест. Для каждого случая фиксируют значения выхода схемы по состоянию реле F. Полученные результаты сравнивают с данными, приведенными в словаре неисправностей (см. таблицу 5). Совпадение состояний выхода реле F и состояний приведенных в столбце словаря неисправностей указывает на неисправность или на класс эквивалентных неисправно­стей, которые соответствуют данному столбцу.

Таблица 5- Словарь неисправностей для Т_д1

Входной набор		F	f1	f2 f4	f3	f5	f6 f8	f7
			при внесении неисправности
№	a b c
2	0 1 0	1	1	0	1	1	1	1
4	1 0 0	0	0	0	0	1	0	0
5	1 0 1	1	1	1	1	1	0	1
6	1 1 0	0	1	0	0	0	0	0

Точное указание неисправности внутри класса эквивалентных неисп­равностей возможно только при измерениях во внутренних точках схемы, соответствующих классу эквивалентных неисправностей.

Диагностический тест второго вида определяется в том случае, если заранее не известно, что тестируемая схема неисправна. В этом случае диагностический тест T_д’ определяется по выражению (1.5)

T_д’ = T_П ·φ _1,2,·φ_1,3 ·…·φ_6,7,· φ_78.

T_д’ = 0·1·2·7·4·6·(0  2  3)(1  2  3  5)(2  3  7)(0  1  5)(1  5  7).

После минимизации полученного выражения получаем множество диагностических тестов. Из результатов анализа полученного множества диагностических тестов следует, что оно содержит один минимальный тест T_д’ = = 0·1·2·4·6·7.

Словарь неисправностей для минимального диагностического теста T_д’ приведен в таблице 6.

Таблица 6- Словарь неисправностей диагностического теста T_д’

Входной набор		F	f1	f2 f4	f3	f5	f6 f8	f7
			при внесении неисправности
№	a b c
0	0 0 0	0	0	0	1	1	0	0
1	0 0 1	1	1	1	1	1	0	1
2	0 1 0	1	1	0	1	1	1	1
4	1 0 0	0	0	0	0	1	0	0
6	1 1 0	0	1	0	0	0	0	0
7	1 1 1	0	1	0	0	0	0	1

Поиск неисправности в схеме осуществляют так же, как и в случае диагностического теста Т_д.

0. Метод цепей и сечений

При расчете тестов на ЭВМ для хранения ТФН из-за ее большого размера требуется большой объем памяти, что снижает размерность решаемых задач. В связи с этим для различных объектов диагноза разработаны специальные модели и методы, которые не имеют универсального характера, но с учетом особенностей объекта позволяют более просто решать задачи построения тестов.

Так, например, для релейно-контактных схем при построении проверяющих тестов используют метод цепей и сечений.

Рисунок 4- Релейно-контактная схема

Под цепью понимают набор состояний контактов, которые обеспечивают наличие цепи проводимости между полюсами схемы.

Под сечением понимают набор состояний контактов, которые обеспечивают разрыв всех цепей схемы.

Рассматриваемая схема (см. рисунок 4) имеет четыре цепи: G₁ = a₁ ,

G₂ = a₁ , G₃ = b , G₄ = с₂ , а также содержит два сечения: H = , H₂ = b c а₂. Все остальные цепи и сечения содержат противоречия, например H₃ = , и поэтому мы их из рассмотрения исключаем.

Перечисление всех цепей и сечений однозначно задает схему. Под цепью, урезанной на каком-то определенном контакте, понимают набор состояний контактов, соответствующий данной цепи, из которого исключен этот контакт. Аналогично определяют сечение, урезанное на каком-то определенном контакте.

Для того чтобы проверить некоторый контакт параллельно-последовательной схемы (рисунок 4) на отсутствие неисправности типа «разрыв», необходимо обеспечить наличие какой-либо цепи, содержащей этот контакт, и обрыв всех других цепей, в которые не входит данный контакт. Тогда при отсутствии неисправности схема будет замкнута, а о наличии неисправности будет свидетельствовать разомкнутое состояние схемы (реле F выключено).

При проверке некоторого контакта на отсутствие неисправности типа «короткое замыкание» необходимо обеспечить разрыв всех цепей схемы и наличие хотя бы одной цепи, разорванной только на данном контакте. Тогда при отсутствии неисправности схема будет разомкнута, а о наличии неисправности будет свидетельствовать замкнутое состояние схемы.

В алгоритм вычисления проверяющей функции какого-то определенного контакта для неисправности типа «разрыв» (φ°) выписывают все цепи, содержащие этот контакт и все сечения, содержащие этот контакт, определяют все сечения, урезанные на этом контакте. Каждую выписанную цепь рассматривают в сочетании с каждым урезанным сечением. Для них определяют входные наборы, на которых они одновременно существуют. Проверяющую функцию φ° находят как объединение всех полученных наборов.

Алгоритм вычисления проверяющей функции для короткого замыкания (φ¹) аналогичен алгоритму вычисления проверяющей функции для неисправности типа «разрыв», только термин «цепь» необходимо заменить на термин «сечение».

Для контакта «a₁» определяем проверочную функцию φ°_a1.

Контакт «а₁» входит в цепи G₁= a₁ и G₂ = a₁ , а также в сечение H = . Сечение, урезанное на контакте а₁, равно H₁/a₁ = .

Рассмотрим сочетание цепи G₁=a₁ с сечением H₁/a₁ = .

Цепь G1 существует при подаче входных переменных а = 1, b = 0, а сечение H1/а – при b = 0, c = 0, т.е. цепь G1 и сечение H1/a одновременно существуют на наборе .

Затем рассматриваем цепь G2 и сечение H1/a₁ = . Цепь G₂ = a₁ существует при наборе а = 1, с = 0, а сечение H₁/a₁, урезанное на контакте a₁, существует при наборе b = 0, с = 0, т.е. цепь G₂ и H₁/a₁ одновременно существуют при таком же наборе переменных а , как и G₁ и H₁/a₁.

Таким образом, φ_a1° = а .

Для контакта a₁ определяем проверочную функцию φ_а1¹. Контакт a₁ входит в сечение H = и цепи G₁ = a₁ и G₂ = a₁ . Цепи G₁ и G₂, урезанные на контакте a₁, соответственно равны G₁/a₁ = , G₂/a₁ = .

Рассмотрим сечение H и цепь, урезанную на контакте a₁ - G₁/a₁. Сечение H существует при значениях переменных а = 0, b = 0, с = 0, а цепь, урезанная на контакте G₁/a₁, существует при b = 0.

Таким образом, H и G₁/a₁ существуют одновременно на наборе .

Затем рассматриваем сечение H и цепь, урезанную на контакте a₁, G₂/a₁. Сечение H существует при наборе а = 0, b = 0, с = 0, а цепь G₂/a₁ - при значении с = 0, т.е. сечение H и цепь G₂/a₁ существуют одновременно также на наборе .

Таким образом, проверяющая функция - φ_а¹ = .

Определяем проверяющие функции для контакта .

Вычисляем проверяющую функцию - φº . Контакт входит в цепь

G₃ = b , и сечение H = . Сечение H , урезанное на контакте , равно

H₁/b₁ = .

Цепь G₃ и сечение H₁/b₁ одновременно существуют на наборе а = 0, b = 1, с = 0, т.е. проверяющая функция - φº = b

Вычисляем проверяющую функцию - φ¹ .

Контакт входит в сечение H = и в цепь G₃ = b . Цепь G₃, урезанная на контакте , G3/ b = . Сечение H и урезанная на контакте цепь - G3/ b одновременно существуют на наборе а = 0, b = 0, с = 0.

Таким образом, проверяющая функция - φ¹ = .

Определяем проверяющие функции - φº φ¹ .

Вычисляем проверяющую функцию φº .

Контакт входит в цепь G₄ = с₂ и в сечение H₁ = . Сечение H₁, урезанное на контакте , H₁/ = . Цепь G₄ и урезанное сечение H₁/ одновременно существуют на наборе , т.е. φº = .

Вычисляем проверяющую функцию φ¹ .

Контакт входит в сечение H₁ = и в цепь G₄ = с₂ . Цепь G₄, урезанная на контакте , G₄/ = . Они одновременно существуют на наборе , т.е. - φ¹ = .

Определяем проверяющие функции для контакта b₂ - φº и φ¹ .

Вычисляем проверяющую функцию φº . Контакт входит в цепь G₁ = a₁ и сечение H₂ = а₂ b c . Сечение H₂, урезанное на контакте , равно H₂/b₂ = а₂ c . Цепь G₁ = a₁ существует на наборе входных переменных а = 1, в = 0, а сечение H₂, урезанное на контакте , H₂/b₂ = а₂ c существует на наборе а = 1, с = 1, т.е. цепь G₁ и сечение H₂, урезанное на контакте , одновременно существуют на наборе а = 1, в = 0, с = 1.

Таким образом, проверяющая функция - φº = а с

Вычисляем проверяющую функцию φ¹ .

Контакт входит в сечение H₂ = а₂ b c и цепь G₁ = a₁ . Цепь G₁, урезанная на контакте , равна G₁/ = a₁.

Рассмотрим сечение H₂ и цепь, урезанную на контакте , G₁/ . Сечение H₂ существует при значениях переменных а = 1, b = 1, с = 1, а цепь, урезанная на контакте , G₁/ существует при а = 1.

Таким образом, H₂ = а₂ b c и G₁/ существуют одновременно на наборе а b c – следовательно, проверяющая функция - φ¹ = а b c.

Определяем проверяющие функции - φº φ¹ .

Вычисляем проверяющую функцию - φº .

Контакт с₁ входит в цепи G₂ = a₁ , G₃ = b и сечение H₂ = b c а₂. Сечение H₂, урезанное на контакте с₁, равно H₂/с₁ = b а₂.

Рассмотрим цепь G₂ = a₁ и сечение H₂, урезанное на контакте с₁, H₂/с₁. Они одновременно существуют на наборе входных переменных а = 1, b = 1, с = 0, т.е. – а b .

Рассмотрим цепь G₃ = b и сечение H₂, урезанное на контакте с₁, H₂/с₁. Они одновременно существуют на наборе входных переменных а = 1, b = 1, с = 0, т.е. – а b .

Следовательно, проверяющая функция φº = а b .

Вычисляем проверяющую функцию φ¹ .

Контакт с₁ входит в сечение H₂ = а₂ b c и цепи G₂ = a₁ , G₃ = b . Цепь G₂, урезанная на контакте с₁, равна G₂/с₁ = a₁. Цепь G₃, урезанная на контакте с₁ , равна G₃/ с₁ = b .

Рассмотрим сечение H₂ и цепь, урезанную на контакте с₁, G₂/с₁. Сечение H₂ существует при значениях переменных а = 1, b = 1, с = 1, а цепь, урезанная на контакте с₁, G₂/с₁ существует при b = 1, т. е. на наборе а b c.

Рассмотрим сечение H₂ и цепь, урезанную на контакте с₁ , G₃/с₁. Они одновременно существуют на наборе а b c.

Таким образом, проверяющая функция - φ¹ = а b c.

Далее определяем проверяющие функции - φº и φ¹ .

Вычисляем проверяющую функцию - φº .

Контакт входит в цепи G₄ = с₂ и сечение H₂ = b c а₂. Сечение H₂, урезанное на контакте , равно H₂/ = b а₂.

Рассмотрим цепь G₂ = с₂ и сечение H₂, урезанное на контакте , H₂/ . Они одновременно существуют на наборе входных переменных а = 0, b = 1, с = 1, т.е. – b с, следовательно, проверяющая функция - φº = b с.

Вычисляем проверяющую функцию φ¹ .

Контакт входит в сечение H₂ = а₂ b c и цепь G₄ = с₂ ,. Цепь G₄, урезанная на контакте , равна G₄/ = с₂ .

Рассмотрим сечение H₂ и цепь, урезанную на контакте , G₄/ . Сечение H₂ существует при значениях переменных а = 1, b = 1, с = 1, а цепь, урезанная на контакте , G₄/ существует при с = 1, т. е. на наборе а b c.

Следовательно, проверяющая функция - φ¹ = а b c.

После определения проверяющих функций для всех контактов схемы определяем проверяющий тест Т_п, который находится как логическое произведение проверяющих функций

Т_п = φ°_a1· φ¹_a1·φ°_b1·φ¹ _b1· φ°_c2 · φ¹_c2 ·φ° ·φ¹ · φ°_c1 · φ¹_c1· φ°_a2· φ¹_a2 ; (6)

Подставляем полученные значения, проверяющих функций в выражение (6) и производим его минимизацию.

Т_п = a · · b · · с · · с ·abc · a b · abc · bc· abc =

= a · · b · с ·abc · a b · bc;

Таким образом, проверочный тест для представленной на рисунке 4 релейно-контактной схемы будет представлять множество входных наборов

Т_п = {a , , b , с, abc, a b , bc}

Вариант задания для определения проверочного теста с использованием метода цепей и сечений выбирают согласно приложению Б.

3. Построение тестов для комбинационных схем на логических

элементах

Логический элемент представляет собой устройство, имеющее n входов и один выход, на котором реализуется некоторая функция алгебры логики (ФАЛ) F(x) (рисунок 5). Неисправность во внутренней структуре логического элемента приводит к тому, что на его выходе вместо функции F(x) реализуется функция неисправности f(x).

х₁

· F(x)

·

·

х_n

Рисунок 5 - Логический элемент

Для логических элементов число и вид неисправности зависят от внутренней структуры элемента. Неисправности логических элементов подразделяются на константные и неконстантные. Константную неисправность можно рассматривать как фиксацию в константу (нуль или единицу) сигнала на входе или выходе элемента. Среди множества константных неисправностей можно выделить эквивалентные и импликантные неисправности.

Эквивалентными неисправностями называются такие неисправности, для которых по состоянию выхода элемента невозможно определить, где конкретно имеет место неисправность – на каком входе или выходе.

Классы эквивалентных неисправностей для логических элементов ИЛИ, И, И-НЕ, ИЛИ-НЕ приведены на рисунке 6 в виде графов, нанесенных на изображение элементов. Эквивалентные неисправности соединены прямыми линиями.

Неисправность N_i находится в отношении импликации к неисправности N_j (обозначается: N_i →N_j), если на тех входных наборах, на которых равна единице проверяющая функция неисправности φ_i = F f_i (f_i функция соответствующая неисправности N_i) , равна единице и проверяющая функция неисправности N_j φ_j (φ_i → φ_j). Отношение импликации показывают на изображении элементов в виде направленного графа от N_i к N_j.

На рисунке 7 показаны отношения импликации неисправностей для логических элементов И, ИЛИ, И-НЕ, ИЛИ-НЕ.

Комбинационная схема содержит логические элементы и связи между ними. В ней возможны следующие дефекты: неисправности логических элементов (ЛЭ), обрывы соединений, замыкания между соединениями, перепутывание связей.

Неисправности комбинационных схем делят на две группы. Неисправность называют правильной, если содержащая ее комбинационная схема остается в классе схем без памяти. Если же в результате внесения неисправности комбинационная схема превращается в схему с памятью, то такую неисправность называют неправильной.

Правильные неисправности подразделяются на константные и неконстантные. Для константных неисправностей характерно следующее свойство: функция, реализуемая неисправной схемой, может быть получена из функции исправной схемы фиксацией в нуль или единицу ее отдельных букв или входящих в нее сложных выражений. Все неисправности, не удовлетворяющие этому условию, относят к классу неконстантных неисправностей.

В настоящей курсовой работе требуется построить проверяющий и диагностический тесты относительно множества константных неисправностей.

Согласно варианту задания, которое представлено в виде ФАЛ, F={1,2,3,5}a,b,c минимизируем её с помощью карты Карно (рисунок 8) и запишем в аналитическом виде.

Рисунок 8 - Карта Карно ФАЛ F={001,010,011,101}

В схеме реализуется функция

Рассмотрим построение проверяющего теста комбинационной схемы относительно константных неисправностей. Для этого по заданной ФАЛ вычерчиваем схему с указанием всех логических элементов и связей между ними (рисунок 9). Комбинационная схема реализует функцию

При этом на схеме укажем компоненты и все неисправности компонент. Под компонентами понимают входы и выходы элементов и входы схемы. Входы схемы, выходы элементов, если они соединены со входом только одного элемента, рассматривают как одну компоненту. Если в схеме имеется точка разветвления, то в качестве компонент считаются как точки разветвления, так и все ветви разветвления.

Для каждой компоненты наносим две константные неисправности К→ 1, К→ 0.

Данная схема имеет 10 компонент и 20 неисправностей.

На каждый логический элемент наносим графы эквивалентных

Рисунок 9 - Комбинационная схема, реализующая функцию

неисправностей (см. рисунок 6) и отношения импликации между неисправностями (см. рисунок 7), т.е. устанавливаем отношения между всеми неисправностями схемы.

Затем нумеруем неисправности, при этом среди эквивалентных неисправностей нумеруем только одну, ближе всех расположенную к выходу. Все неисправности, к которым направлены дуги, не нумеруют, а если дуга направлена к одной из эквивалентных неисправностей, то ни одну из них не нумеруют.

В результате выполнения данной операции сокращаем список неисправностей, которые рассматриваем при построении теста. В данной схеме пронумеровано 8 неисправностей, в то время как исходное множество содержит 20 неисправностей.

Составляем ТФН, в которую включаем все пронумерованные неисправности. ТФН для рассматриваемого примера, вычисленная по приведенным ниже функциям неисправностей, приведена в таблице 7. Функции неисправностей рассчитывают методами, которые используются для релейно-контактных схем.

Функции неисправностей:

Таблица 7 – Таблица функции неисправностей

№	Входной набор			F	Функция неисправности
	a	b	c		f1	f2	f3	f4	f5	f6	f7	f8
0	0	0	0	0	0	1	0	0	1	0	1	0
1	0	0	1	1	0	1	1	1	1	1	1	1
2	0	1	0	1	1	1	1	0	1	1	1	0
3	0	1	1	1	1	1	1	0	1	1	1	1
4	1	0	0	0	0	1	0	0	0	0	0	0
5	1	0	1	1	0	1	1	1	1	1	0	1
6	1	1	0	0	0	0	0	0	0	1	0	0
7	1	1	1	0	0	0	1	0	0	1	0	1

Вычисляем проверяющие функции в соответствии с выражением (1.1):

Затем в соответствии с выражением (1.2) вычисляется проверяющий тест.

Т_п = φ₁ ·φ₂·φ₃·φ₄·φ₅·φ₆·φ₇·φ₈;

Подставляем в выражение для проверяющего теста полученные проверочные функции и минимизируем полученное выражение -

Т_п = (1 5)·(0  4)·7· (2  3) · 0 · (6  7)· (0  5)· )·(2  7) =0·7· (1 5) · (2  3).

В результате получаем четыре минимальных теста: Т_п1 = 0 ·1·2·7;

Т_п2 = 0 ·1·3·7; Т_п3 = 0 ·2·5·7; Т_п4 = 0 ·3 ·5 ·7;

Вычисление диагностического теста

Диагностический тест комбинационных схем рассчитывают методом аналогичным методу, применяемому для определения проверочного теста, но при этом не учитывают отношения импликации между неисправностями. На схему наносят только графы эквивалентных неисправностей, которые нумеруют в соответствии с указанным для них правилом. В результате, число неисправностей, включаемых в ТФН, увеличивается, так в данном случае дополнительно в ТФН включаются две неисправности выхода схемы, которым соответствуют функции неисправностей (f₉ = 1, f₁₀ = 0)..

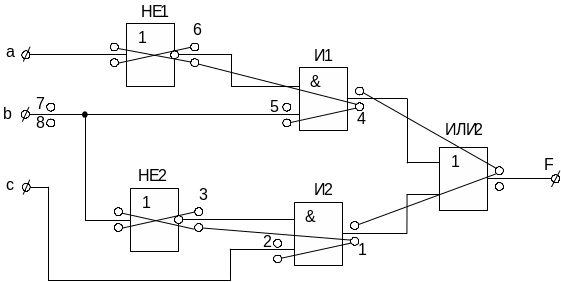
Рисунок 10 - Эквивалентные неисправности комбинационной схемы

Представленным на рисунке 10 неисправностям соответствует таблица функций неисправностей (таблица 8).

По данной таблице определяем диагностический тест. Для каждой пары неисправностей вычисляем различающую функцию в соответствии с выражением (1.3):

Таблица 8 - Таблица функций неисправности

№	Входной набор			F	Функция неисправности
	a	b	c		f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
0	0	0	0	0	0	1	0	0	1	0	1	0	1	0
1	0	0	1	1	0	1	1	1	1	1	1	1	1	0
2	0	1	0	1	1	1	1	0	1	1	1	0	1	0
3	0	1	1	1	1	1	1	0	1	1	1	1	1	0
4	1	0	0	0	0	1	0	0	0	0	0	0	1	0
5	1	0	1	1	0	1	1	1	1	1	0	1	1	0
6	1	1	0	0	0	0	0	0	0	1	0	0	1	0
7	1	1	1	0	0	0	1	0	0	1	0	1	1	0

φ_1,2 = 0  1  4  5; φ_1,3 = 1  5  7; φ_1,4 = 1  2  3  5; φ_1,5 = 0  1  5;

φ_1,6 = 1  5  6  7; φ_1,7 = 1  2; φ_1,8 = 1  2  5  7; φ_1,9 = 0  1  4  5  6  7;

φ_1,10 = 2  3;

φ_2,3 = 0  4  7; φ_2,4 = 0  2  3  4; φ_2,5 = 4; φ_2,6 = 0  4  6  7;

φ_2,7 = 4  5; φ_2,8 = 0  2  4  7; φ_2,9 = 6  7; φ_2,10 = 0  1  2  3  4  5;

φ_3,4 = 2  3  7; φ_3,5 = 0  7; φ_3,6 = 6; φ_3,7 = 1  5  7; φ_3,8 = 2;

φ_3,9 = 0  4  6; φ_3,10 = 1  2  3  5  7;

φ_4,5 = 0  2  3; φ_4,6 = 2  3  6  7; φ_4,7 = 0  2  3  5; φ_4,8 = 3  7;

φ_4,9 = 0  2  3  4  6  7; φ_4,10 = 1  5;

φ_5,6 = 0  6  7; φ_5,7 = 5; φ_5,8 = 0  2  7; φ_5,9 = 4  6  7;

φ_5,10 = 0  1  2  3  5;

φ_6,7 = 0  5  6  7; φ_6,8 = 2  6; φ_6,9 = 0  4; φ_6,10 = 1  2  3  5  6  7;

φ_7,8 = 0  2  5  7; φ_7,9 = 4  5  6  7; φ_7,10 = 0  1  2  3;

φ_8,9 = 0  2  4  6; φ_8,10 = 1  3  5  7;

φ_9,10 = 0  1  2  3  4  5  6  7;

В соответствии с выражением (1.4 )вычисляем диагностический тест Тд : Т_д= φ_1,2·φ_1,3·…·φ_8,10·φ_9,10

Т_д = (0  1  4  5) (1  5  7) (1  2  3  5)( 0  1  5) (1  5  6  7)&

&(1  5  6  7) (1  2) (1  2  5  7) (0  1  4  5  6  7) (2  3)&

& (0  4  7) (0  2  3  4) 4 (0  4  6  7) ( 4  5) (0  2  4  7)(6  7)& &(0  1  2  3  4  5) (2  3  7) (0  7) 6 (1  5  7) 2 (0  4  6)&

&(1  2  3  5  7) (0  2  3) (2  3  6  7) (0  2  3  5) (3  7) (0  2  3  4  6  7) ( 1  5) (0  6  7) 5 (0  2  7) (4  6  7) (0  1  2  3  5) & & (0  5  6  7) ( 2  6) ( 0  4) (1  2  3  5  6  7) (0  2  5  7) (4  5   6  7) (0  1  2  3) ( 0  2   4  6) (1  3  5  7) (0  1  2  3  4  5   6  7);

В результате минимизации полученного выражения получаем

Т_д = 2·4·5·6·(0  7) (3  7). Это выражение содержит один минимальный тест Т_д = 2·4·5·6·7.

Для поиска конкретной неисправности в соответствии с полученным выражением Т_д используется словарь неисправностей (таблица 9).

Таблица 9 - Словарь неисправностей для Т_д.

№	Входной набор			F	Функция неисправности
	a	b	c		f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
2	0	1	0	1	1	1	1	0	1	1	1	0	1	0
4	1	0	0	0	0	1	0	0	0	0	0	0	1	0
5	1	0	1	1	0	1	1	1	1	1	0	1	1	0
6	1	1	0	0	0	0	0	0	0	1	0	0	1	0
7	1	1	1	0	0	0	1	0	0	1	0	1	1	0

Второй вариант нахождения диагностического теста:

Тд' = Тп · φ_1,2·φ_1,3·…·φ_8,10·φ_9,10 .

Тд' = 0·3·5·7·2·4·5·6 · (0  7) (3  7). Полученное выражение содержит один минимальный диагностический тест Тд' = 0·2·3·4·5·6·7.

Словарь неисправностей для этого диагностического теста представлен в таблице 10.

Таблица 10 - Словарь неисправностей для диагностического теста Тд'

№	Входной набор			F	Функция неисправности
	a	b	c		f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
0	0	0	0	0	0	1	0	0	1	0	1	0	1	0
2	0	1	0	1	1	1	1	0	1	1	1	0	1	0
3	0	1	1	1	1	1	1	0	1	1	1	1	1	0
4	1	0	0	0	0	1	0	0	0	0	0	0	1	0
5	1	0	1	1	0	1	1	1	1	1	0	1	1	0
6	1	1	0	0	0	0	0	0	0	1	0	0	1	0
7	1	1	1	0	0	0	1	0	0	1	0	1	1	0