Образец выполнения задачи с1
Условия задачи. Жесткая рама ADEB закреплена на двух опорах: A (подвижный шарнир) и B (неподвижный шарнир).
На раму действуют заданные активные силы:
- сосредоточенная сила F величиной 25 кН, приложенная в точке D;
- пара сил с моментом М = 50 кН·м;
- нагрузка, равномерно распределенная на участке EB, интенсивностью q = 2 кН/м.
Расчетная схема задачи показана на рис. 2.12.
Определить реакции опор А и В, приняв размер а = 0,5 м.
Решение. Рассмотрим равновесие рамы ADEB. На расчетной схеме покажем действующие на раму активные силы. Нагрузку, равномерно распределенную на участке ЕВ, заменим ее равнодействующей силой Q, величина которой
Q = q·ЕВ = q·2а = 20 кН/м·1м = 20 кН,
а линия действия проходит через середину участка ЕВ. Освободим раму от связей, наложенных в точках А и В, заменив эти связи силами реакций. Реакцию RB неподвижного шарнира В, направление которой неизвестно, разложим на две составляющие: горизонтальную XB и вертикальную YB. Реакцию RА катковой опоры (подвижного шарнира) А направим перпендикулярно опорной плоскости катков (рис. 2.12).
Р
ис. 2.12
Для составления уравнений равновесия введем координатные оси х. у и выберем в качестве моментной точку В, через которую проходят линии действия двух неизвестных реакций XВ и YВ .
Запишем уравнения проекций сил на оси x и y:
;
. (С1.1)
;
. (С1.2)
Действующая на раму пара сил в уравнениях проекций не учитывается, поскольку сумма проекций сил пары на любую ось равна нулю.
Запишем уравнение моментов сил относительно точки В:
;
. (С1.3)
В уравнении (С1.3) для вычисления момента
силы F относительно
точки В была применена теорема
Вариньона. Сила F была
разложена на две составляющие: F
= F' + F'' (рис. 2.12), величины
которых
,
.
После этого момент силы F
был найден как сумма моментов этих
составляющих:
.
Подставим в составленные уравнения равновесия (С1.1)-(С1.3) числовые значения заданных величин:
;
;
. (С1.4)
Решив систему линейных уравнений (С1.4), найдем числовые значения искомых реакций.
Ответ: RА = 1,4 кН, ХВ = 12,5 кН, YВ = - 2,7 кН (отрицательный знак указывает, что вектор силы реакции YВ имеет направление, противоположное изображенному на рис. 2.12).
2.10. Задача с2 для расчетно-графических заданий
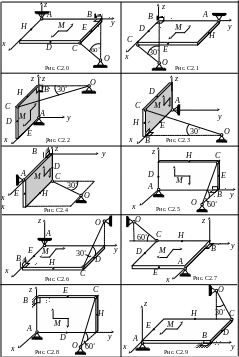
Однородная прямоугольная плита со сторонами AB = 3a, BC = 2а весом P = 3 кН неподвижно закреплена при помощи трех опор: сферического шарнира в точке A; цилиндрического шарнира (шарнирной петли) в точке B; невесомого опорного стержня CO в точке C (рис. С2.0-С2.9).
На плиту действуют: пара сил с моментом М = 5 кН·м, лежащая в плоскости плиты; сосредоточенные силы F1, F2, F3 и F4, величины, направления и точки приложения которых указаны в табл. С2.
Определить реакции опор A, B и C. При окончательных подсчетах принять а = 0,8 м.
Указания. С2 – задача на составление уравнений равновесия (2.3), которые выражают необходимые и достаточные условия равновесия свободного твердого тела, находящегося под действием пространственной системы сил. Поэтому, чтобы воспользоваться ими, необходимо предварительно освободить плиту от наложенных на нее связей, заменив их силами реакций.
Реакция RA сферического шарнира А – это сила, имеющая неизвестные направление и величину. Удобно представить ее в виде трех взаимно перпендикулярных составляющих XA, YA, ZA . Реакция RВ цилиндрического шарнира (шарнирной петли) B направлена перпендикулярно оси шарнира, поэтому ее следует разложить на две составляющие, лежащие в плоскости, перпендикулярной оси шарнира.
При вычислении моментов силы Fi (i = 1, 2, …4) относительно координатных осей вектор силы следует разложить на две составляющие Fi', Fi'', параллельные координатным осям, а затем воспользоваться теоремой Вариньона (о моменте равнодействующей). Например,
.
