Реальная математика.

Ре­ше­ние.

Про­ве­рим каж­дое из утвер­жде­ний.

1) «Если про­ти­во­по­лож­ные углы вы­пук­ло­го че­ты­рех­уголь­ни­ка равны, то этот че­ты­рех­уголь­ник — па­рал­ле­ло­грамм.» — верно, если в че­ты­рех­уголь­ни­ке про­ти­во­по­лож­ные углы равны, то этот че­ты­рех­уголь­ник — па­рал­ле­ло­грамм.

2) «Если сумма трех углов вы­пук­ло­го че­ты­рех­уголь­ни­ка равна 200°, то его чет­вер­тый угол равен 160°.» — верно, Сумма углов вы­пук­ло­го четырёхуголь­ни­ка равна 360°.

3) «Сумма двух про­ти­во­по­лож­ных углов че­ты­рех­уголь­ни­ка не пре­вос­хо­дит 180°.» — не­вер­но, сумма про­ти­во­по­лож­ных углов че­ты­рех­уголь­ни­ка боль­ше 180°.

4) «Если ос­но­ва­ния тра­пе­ции равны 4 и 6, то сред­няя линия этой тра­пе­ции равна 10.» — не­вер­но, сред­няя линия тра­пе­ции равна по­лу­сум­ме ос­но­ва­ний.

 

Ответ: 1; 2.

Ответ: 1; 2

14. В таб­ли­це даны ре­зуль­та­ты олим­пи­ад по ис­то­рии и об­ще­ст­во­зна­нию в 10 «А» клас­се.

Номер уче­ни­ка	Балл по ис­то­рии	Балл по об­ще­ст­во­зна­нию
5005	45	76
5006	34	23
5011	67	56
5015	78	67
5018	59	79
5020	46	32
5025	54	76
5027	95	88
5029	46	72
5032	83	45
5041	48	66
5042	28	42
5043	63	67
5048	92	83
5054	38	64

 

По­хваль­ные гра­мо­ты дают тем школь­ни­кам, у кого сум­мар­ный балл по двум олим­пи­а­дам боль­ше 130 или хотя бы по од­но­му пред­ме­ту на­бра­но не мень­ше 70 бал­лов. Сколь­ко че­ло­век из 10 «А», на­брав­ших мень­ше 60 бал­лов по ис­то­рии, по­лу­чат по­хваль­ные гра­мо­ты?

1)5 2)2 3)3 4) 4

Ре­ше­ние.

Вы­де­лим тех, кто пло­лу­чил менее 60 бал­лов по ис­то­рии:

 

 

Из них те, кто ука­зан под но­ме­ра­ми 5005, 5025, 5029 на­бра­ли более 70 бал­лов по об­ще­ст­во­зна­нию. А более 130 бал­лов по­лу­чи­ли по двум олим­пи­а­дам те, кто участ­во­вал под но­ме­ра­ми 5005, 5025 и 5018. Таким об­ра­зом, таких участ­ни­ков чет­ве­ро.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

15. 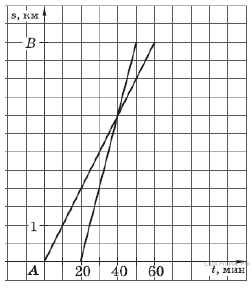Из пунк­та     в пункт     вышел пе­ше­ход, и через не­ко­то­рое время вслед за ним вы­ехал ве­ло­си­пе­дист. На ри­сун­ке изоб­ра­же­ны гра­фи­ки дви­же­ния пе­ше­хо­да и ве­ло­си­пе­ди­ста. На сколь­ко ки­ло­мет­ров в час ско­рость пе­ше­хо­да мень­ше ско­ро­сти ве­ло­си­пе­ди­ста?

Ре­ше­ние.

Пе­ше­ход про­шел путь до места встре­чи за 40 мин или часа. Ве­ло­си­пе­дист про­ехал этот же путь за 20 мин или часа. Таким об­ра­зом, ско­рость пе­ше­хо­да равна км/ч, а ско­рость ве­ло­си­пе­ди­ста км/ч.

Таким об­ра­зом, ско­рость пе­ше­хо­да мень­ше ско­ро­сти ве­ло­си­пе­ди­ста на 6 км/ч.

Ответ: 6

16. В те­че­ние ав­гу­ста по­ми­до­ры по­де­ше­ве­ли на 50%, а затем в те­че­ние сен­тяб­ря по­до­ро­жа­ли на 70%. Какая цена мень­ше: в на­ча­ле ав­гу­ста или в конце сен­тяб­ря — и на сколь­ко про­цен­тов?

Ре­ше­ние.

Обо­зна­чим на­чаль­ную цену по­ми­до­ров за x, тогда их цена в сент­бя­ре будет со­став­лять x − 0,5x = 0,5x, цена же в сен­тяб­ре будет со­став­лять 0,5x + 0,7 · 0,5x = 0,85x. Сле­до­ва­тель­но, цена на по­ми­до­ры была ниже в конце сен­тяб­ря, и раз­ни­ца со­став­ля­ла 15%.

 

Ответ: 15.

Ответ: 15

17. Сколь­ко спиц в ко­ле­се, если угол между со­сед­ни­ми спи­ца­ми равен 18°?

Ре­ше­ние.

Ко­ле­со пред­став­ля­ет собой круг. Ко­ли­че­ство спиц сов­па­да­ет с ко­ли­че­ством сек­то­ров на ко­то­рые ими оно де­лит­ся. Так как развёрну­тый угол 360°, а угол между спи­ца­ми равен 18°, имеем: По­это­му спиц в ко­ле­се 20 штук.

 

Ответ: 20.

Ответ: 20

18. На диа­грам­ме пред­став­ле­но рас­пре­де­ле­ние ко­ли­че­ства поль­зо­ва­те­лей не­ко­то­рой со­ци­аль­ной сети по стра­нам мира. Всего в этой со­ци­аль­ной сети 9 млн поль­зо­ва­те­лей.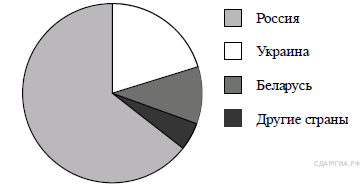 Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

 

1) Поль­зо­ва­те­лей из Бе­ла­ру­си мень­ше, чем поль­зо­ва­те­лей из Укра­и­ны.

2) Поль­зо­ва­те­лей из Рос­сии боль­ше 4 мил­ли­о­нов.

3) Поль­зо­ва­те­лей из Укра­и­ны боль­ше чет­вер­ти об­ще­го числа поль­зо­ва­те­лей.

4) Поль­зо­ва­те­лей из Бе­ла­ру­си боль­ше, чем поль­зо­ва­те­лей из Фин­лян­дии.

 

В от­ве­те за­пи­ши­те номер вы­бран­но­го утвер­жде­ния.

Ре­ше­ние.

Разъ­яс­ним каж­дый ва­ри­ант от­ве­та.

 

1) Оче­вид­но, что поль­зо­ва­те­лей из Бе­ла­ру­си мень­ше, чем поль­зо­ва­те­лей из Укра­и­ны.

 

2) Видно, что поль­зо­ва­те­лей из Рос­сии боль­ше по­ло­ви­ны всех поль­зо­ва­те­лей, зна­чит, боль­ше 9/2 = 4,5 млн, а зна­чит, боль­ше 4 мил­ли­о­нов.

 

3) Сек­тор в чет­верть диа­грам­мы от­се­ка­ет­ся углом в 360°/4 = 90°. Оче­вид­но, что угол, от­се­ка­ю­щий сек­тор «Укра­и­на» мень­ше 90°, зна­чит, мень­ше чет­вер­ти поль­зо­ва­те­лей сети — из Укра­и­ны.

 

4) Сек­тор «Бе­ла­русь» за­ни­ма­ет боль­шую пло­щадь диа­грам­мы, чем сек­тор «Дру­гие стра­ны», а т. к. «Фин­лян­дия» вклю­че­на в «Дру­гие стра­ны», имеем: поль­зо­ва­те­лей из Бе­ло­рус­сии боль­ше, чем поль­зо­ва­те­лей из Фин­лян­дии.

Ответ: 3.

Ответ: 3

19. В фирме такси в дан­ный мо­мент сво­бод­но 20 машин: 9 чер­ных, 4 жел­тых и 7 зе­ле­ных. По вы­зо­ву вы­еха­ла одна из машин, слу­чай­но ока­зав­ша­я­ся ближе всего к за­каз­чи­ку. Най­ди­те ве­ро­ят­ность того, что к нему при­е­дет жел­тое такси.

Ре­ше­ние.

Ве­ро­ят­ность того, что при­е­дет жел­тая ма­ши­на равна от­но­ше­нию ко­ли­че­ства жел­тых машин к об­ще­му ко­ли­че­ству машин:

Ответ: 0,2.

Ответ: 0,2

20. В фирме «Эх, про­ка­чу!» сто­и­мость по­езд­ки на такси (в руб­лях) рас­счи­ты­ва­ет­ся по фор­му­ле C = 150+11 ⋅ (t − 5) , где t — дли­тель­ность по­езд­ки, вы­ра­жен­ная в ми­ну­тах (t > 5). Поль­зу­ясь этой фор­му­лой, рас­счи­тай­те сто­и­мость 14-ми­нут­ной по­езд­ки.