1.6. Укороченные циклические коды

Поскольку ЦК порождаются делителями бинома Х ⁿ +1 (4.3), то для большей части значений n и k имеется относительно мало кодов, удов- летворяющих всем свойствам, присущим ЦК (подразд. 1.4). Поэтому естественно попытаться найти среди линейных кодов такие, которые хотя и не являются в действительности циклическими, обладают похо- жей математической структурой и столь же легко реализуются.

При разработке систем передачи информации, работающих с дискрет- ными сигналами в предположении необходимости исправления (обнару- жения) ошибок, число информативных символов k_ выбирают, как пра-

^{вило, таким, чтобы оно было кратным длине первичного кода k}₁^:

k_ = а k₁, где а = 1, 2, 3, 4, …,

а значение n_ = k_ + r, где число проверочных символов должно удов- летворять заданному значению кратности обнаруживаемых и исправля- емых ошибок. В частности, ЭВМ обычно обмениваются машинными

^{словами в виде байтов, состоящих из восьми символов (k}₁ ^{= 8).}

^{При этом n}_ ^{и k}_ ^{часто не совпадают с табулированными [3] ЦК. В}

^{этом случае по таблицам [3] находят ЦК, который соответствует обо-}

снованному значению r = n – k для классического, табулированного ЦК, а затем уменьшают n и k_ до n –l и k – l, получая укороченный ЦК.

Укороченные циклические коды (УЦК) получают из полных ЦК, ис- пользуя для передачи информации только кодовые комбинации полно- го кода, содержащие слева l нулей. Это дает возможность построить УЦК (n – l, k – l) путем исключения первых l столбцов и l строк из порождающей матрицы (4.24). Полученный код не будет строго цикли- ческим, так как циклический сдвиг не всегда будет приводить к получе- нию очередной разрешенной кодовой комбинации. Поэтому укорочен- ные (усеченные) ЦК часто называют псевдоциклическими или квази- циклическими.

Укороченные ЦК сохраняют основные свойства классических ЦК (подразд. 1.4), к числу которых относятся следующие:

1) УЦК образуются делителями бинома Хⁿ + 1-порождающими поли-

номами G(X), такими же, как у полных ЦК;

2) УЦК относятся к классу линейных (групповых) кодов, для кото- рых сумма разрешенных кодовых комбинаций УЦК также является раз- решенной кодовой комбинацией (4.12);

3) УЦК обладает таким же минимальным (конструктивным) кодо- вым расстоянием как у исходного ЦК, и таким же числом проверочных символов (4.21), но не может быть плотноупакованным;

4) УЦК исправляет такое же число ошибок, что и ЦК, т. е. имеет такую же кратность обнаруживаемых и исправляемых ошибок;

5) при построении кодеков УЦК используются те же схемы, что и для классических ЦК, при условии, что каждому усеченному коду спереди приписывается l нулей.

Специфику построения УЦК рассмотрим на следующем примере.

Пример

Передаче подлежит сообщение, закодированное стандартным кодом МТК-2 с числом информационных символов k = 5. Обеспечить у полу- чателя сообщений исправление однократной ошибки в кодовом слове.

Однократная ошибка исправляется при минимальном кодовом рас- стоянии d_min = 3. Этому значению удовлетворяют коды Хемминга (7,4), (15, 11), (31, 26) ... (см. табл. 4.1). Код (7,4) с числом информационных

символов k = 4 не удовлетворяет условию примера при необходимости передачи k = 5. Этому условию удовлетворяет следующий по порядку код Хемминга (15, 11), если из общего числа символов n = 15 и числа информативных символов k = 11 вычесть одно и то же число l = 6 (ис- ключение первых l столбцов и l строк порождающей код матрицы с

x⁴ +x +1

G (15,11) =

¹⁰⁰¹¹ 0000000000

⁰¹⁰⁰¹ 1000000000

⁰⁰¹⁰⁰ 1100000000

⁰⁰⁰¹⁰ 0110000000

⁰⁰⁰⁰¹ 0011000000

1

2

4

l = 6 ³

5

00000 1001100000	6
00000 0100110000	7	100110000	1
00000 0010011000	8	010011000	2
00000 0001001100	9	G (9,5) = 001001100	3
00000 0000100110	10	000100110	4
00000 0000010011	11	000010011	5
l = 6

Усеченная матрица (9,5)

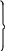(4.30)

размерностью k  n). Получаем УЦК (9, 5), удовлетворяющий условию примера k = 5, d_min = 3, с числом проверочных символов r = 4.

^{Для опорного ЦК (15,11) бином Xn + 1 раскладывается на следую-}

щие неприводимые полиномы:

X ¹⁵ + 1 = (X + 1) (X ² + X + 1) (X ⁴ + X + 1) (X ⁴ + X³ + 1) (X ⁴ + X³ + X ² + X + 1),

из которых для построения кода r = 4 можно выбрать любой из трех последних. Выберем в качестве порождающего полинома G (X) = X⁴ +

+ X + 1 и на основе матрицы этого ЦК (15,11) покажем, как осуществ- ляется отсечка:

Приведем усеченную матрицу G (9,5) к каноническому виду путем соответствующего суммирования строк по аналогии с проводимыми пре- образованиями с матрицами (4.24) и (4.25) и получим соответствую- щие равенства проверки на четность при поэлементном формировании усеченного кода (9,5) (см. (4.27) в качестве аналога):

Обратим внимание на то, что порождающая матрица УЦК G_k (9,5) и соответствующие ей алгоритмы проверки на четность (4.31) полностью совпадают с выражениями (3.22) методических указаний, по которым

10000 0101 1  1  4  5

01000 1011 2  2  5

_{G  00100 1100 3  3}

^r₁ ^{ i}₂ ^{ i}₃^;

r₂  i₁  i₃  i₄ ;

_{k 9,5}

_{r  i  i}

_{ i ;}

_{00010 0110 4  4}

_{3 2 4 5}

₀₀₀₀₁

^ç

E

0011 5  5

^r₄ ^{ i}₁ ^{ i}₂ ^{ i}₅^.

(4.31)

студентами выполнялась ЛР № 3. Таким образом, УЦК (9,5) полностью удовлетворяет условиям примера (с. 114).