2. Визначаємо парність або непарність.
.
Функція
— парна. Подальше дослідження будемо
вести для
.
3. Визначаємо проміжки монотонності.
.
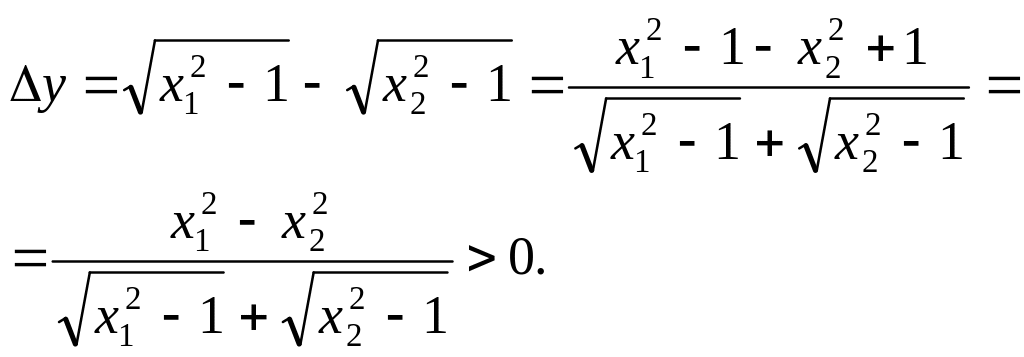
При зростанні значень х від 1 до значення y зростають.
4. Знаходимо корені функції та проміжки знакосталості.
Якщо
,
то
при
.
при
всіх
.
5. Встановлюємо області зміни функції.
Якщо
,
то
.
Якщо
,
то
.
Отже,
.
6. Досліджуємо на опуклість та вгнутість
Легко доводиться нерівність.
,
1 ≤ х1
<
x2.
Графік функції — опукла крива.
7. Будуємо графік функції (рис. 5.33).
Рис. 5.33
І. Побудова графіків функції зсувом графіків основних функцій або осей координат
Нехай
— одна з основних функції, причому
графік її побудований.
1. Щоб
побудувати графік функції
,
достатньо або графік функції
зсунути вздовж осі Oy
на с
одиниць у
бік, що збігається зі знаком с,
або перенести паралельно вісь Ох
у бік,
протилежний знаку с
(рис. 5.34).
2. Щоб
побудувати графік функції
,
можна або графік функції
зсунути вздовж осі Ох
на с
одиниць у
бік, протилежний знаку с,
або перенести паралельно вісь Oу
в бік, який
збігається зі знаком с
(рис. 5.35).
Рис. 5.34 Рис. 5.35
Iі. Побудова графіків функцій симетричним відображенням відносно осей координат графіка основної функції
1.
Щоб побудувати графік функції
,
можна побудувати зображення, симетричне
графіку функції
відносно осі Ох
(рис. 5.36).
2.
Щоб побудувати графік функції
,
можна побудувати зображення, симетричне
графіку функції
відносно осі Oy
(рис. 5.37).
Рис. 5.36
Рис. 5.37
ІІІ. Побудова графіків функцій деформацією графіка основної функції
1.
Щоб побудувати графік функції
при
,
достатньо графік функції
розтягнути вздовж осі Oy,
якщо
,
і стиснути вздовж цієї осі, якщо
(рис. 5.38).
Рис. 5.38
2.
Щоб побудувати графік функції
при
,
достатньо графік функції
стиснути вздовж осі Ох,
якщо
,
і розтягнути вздовж цієї осі, якщо
(рис. 5.39).
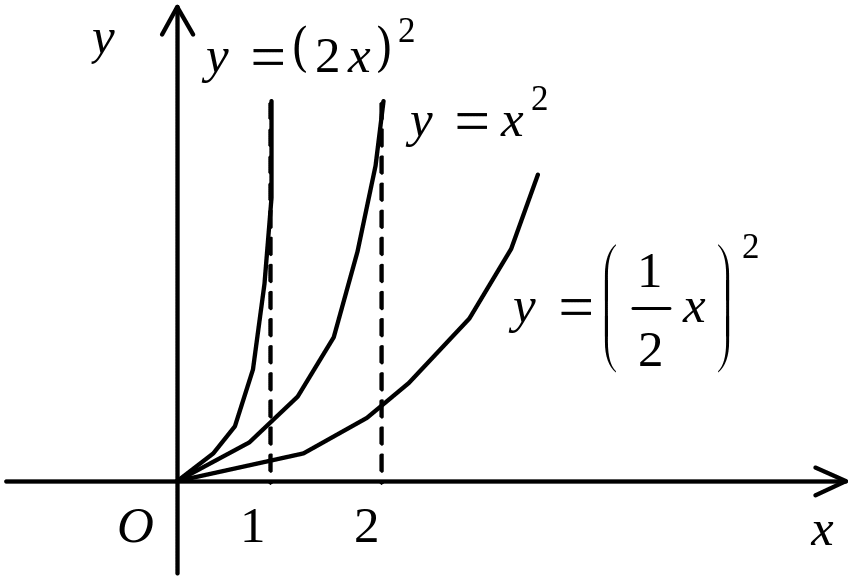
Рис. 5.39
IV. Побудова графіків функцій, аналітичний вираз яких містить знак абсолютної величини
1.
.
Функція
— парна. Щоб побудувати її графік,
достатньо для
побудувати графік функції
,
а потім добудувати його ліву частину,
симетричну правій відносно осі Oy.
1
)
(рис. 5.40).
2)
(рис. 5.41).
Рис. 5.40
Рис. 5.41
2.
y
=
.
Цю функцію можна розглядати як сукупність
двох функцій:
Щоб
побудувати графік функції
,
достатньо побудувати графік функції
,
а далі ту частину графіка, яка розміщена
у нижній частині півплощини, симетрично
відобразити відносно осі Ох.
1
)
(рис. 5.42).
Рис. 5.42
3.
.
Функція
— парна. Можлива така послідовність
побудови графіка цієї функції.
1. Побудувати для графік функції , потім симетрично відобразити його відносно осі Oy, і, нарешті, ту частину здобутого графіка, яка розміщена в нижній півплощині, симетрично відобразити відносно осі Ox.
2. Побудувати для графік функції , а далі ту частину здобутого графіка, яка розміщена в нижній півплощині, симетрично відобразити відносно осі Ох, і, нарешті, здобутий графік симетрично відобразити відносно осі Oy.
(рис.
5.43).
Рис. 5.43
V. Кусково-лінійна функція
Графіком кусково-лінійної функції є ламана лінія. Для побудови графіка знаходять рівняння ланок ламаної.
.
Точки зламу (1, 2, 3, 4, 5) графіка цієї функції такі: х = 1; х = 2; х = 3; х = 4; х = 5 (корені функцій, що входять під знак модуля).
Знаходимо рівняння ламаної.
;
;
;
;
;
.
З
Рис. 5.44
5.7.2. Асимптоти кривої
Означення. Асимптотою кривої називають пряму (або криву) лінію, до якої необмежено наближається точка, рухаючись по кривій у нескінченність.
Рис. 5.45
1. Вертикальні
асимптоти.
Нехай функція
визначена в одному з інтервалів (а; с)
та (с; b),
або на обох із них, причому
с
— скінченне число.
Означення.
Якщо
функція
має в точці с
розрив
другого роду і існує хоча б одна із
нескінченних односторонніх границь
функції
в точці с
(наприклад,
або
,
рис. 5.45), то пряму х = с
називають вертикальною
асимптотою кривої
.
Отже,
усі вертикальні асимптоти виду х = с
кривої
можна знайти, знайшовши скінченне число
точок с,
в яких функція
має розриви другого роду й існує хоча
б одна із нескінченних односторонніх
границь функції f(x)
у точці с.
Ф
ункція
має вертикальну асимптоту
(рис. 5.46), оскільки точка
— точка розриву другого роду:
;
.
Рис. 5.46
Г
рафік
функції
має вертикальні асимптоти
(рис. 5.47).
Рис. 5.47