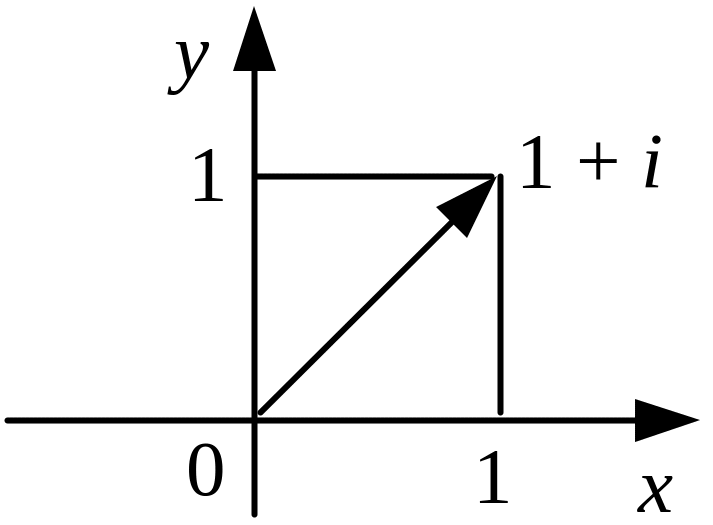1.2.9. Модуль та аргумент комплексного числа

Означення. Модулем комплексного числа а + bі називається вираз який позначається r або |а + bі|.

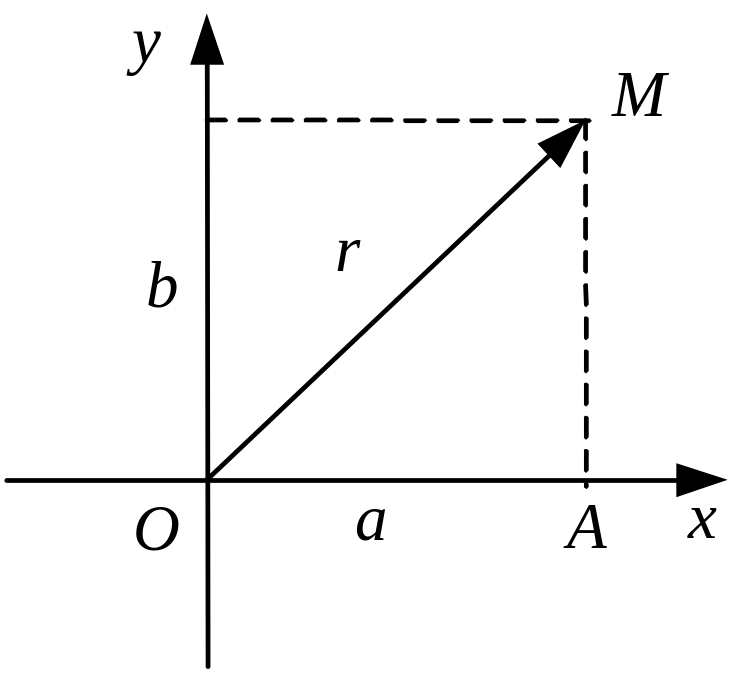
Рис. 1.13

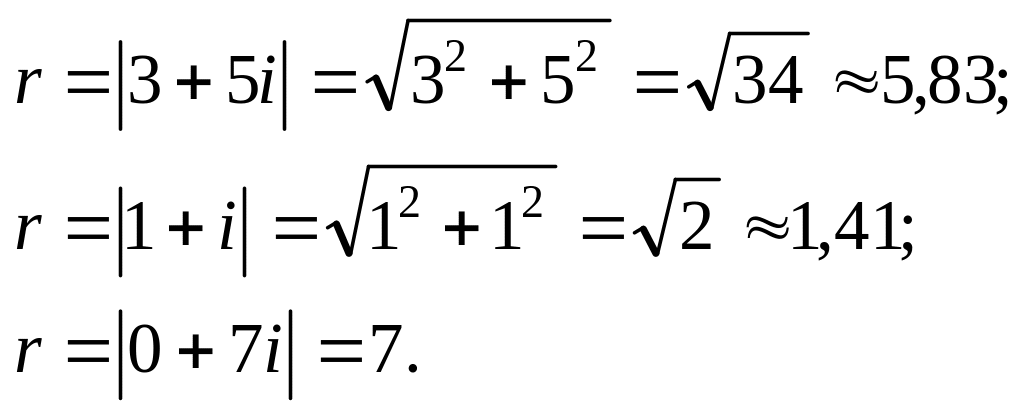
Означення. Кут  між віссю Ох і відрізком ОМ, де точка М зображає комплексне число а + bі, називається аргументом комплексного числа а + bі (рис. 1.13).

Кожне відмінне від нуля комплексне число має нескінченну кількість аргументів, які відрізняються один від одного на 2k. Для числа 0 аргумент не визначений.

А ргумент  комплексного числа а + bі визначається формулами:

(1)

З ауваження. Щоб користуватися цими формулами, потрібно враховувати знаки абсциси та ординати комплексного числа.

З найти аргумент комплексного числа – 3 – 3і.

 За формулою (1) маємо

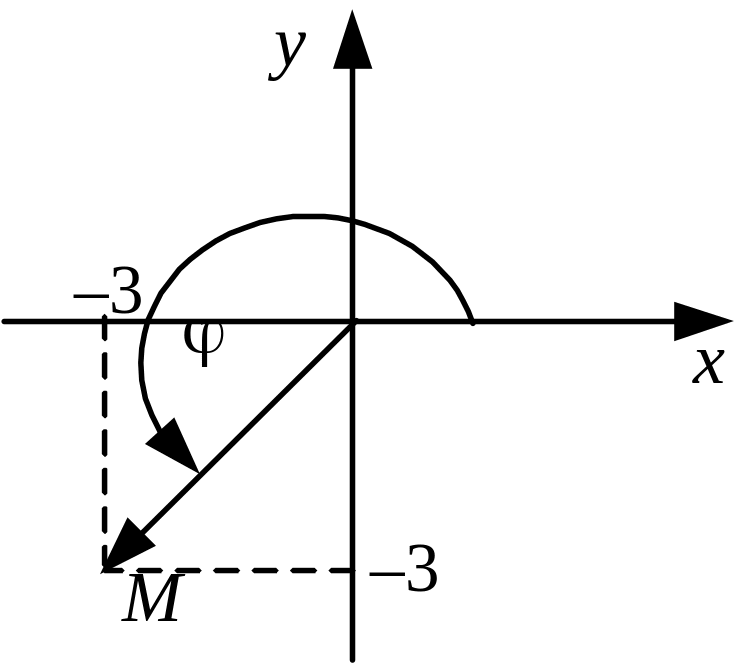
, або  = 45,  = 225 і т. ін. Але кут 45 не є аргументом числа – 3 – 3і (рис. 1.14). Правильною є така відповідь: 225; – 135; 585 і т. д. Цей результат дістаємо, враховуючи, що абсциса та ордината комплексного числа є від’ємними, тобто точка М належить чверті ІІІ.

Рис. 1.14

Означення. Значення аргументу, яке належить проміжку (– ; ), називається головним.

Д ля комплексних чисел – 3 – 3і; 2і; – 5і головне значення аргументу дорівнює – 135; 90; – 90.

З ауваження. Аргумент дійсного додатного числа має головне значення 0; від’ємного числа 180. Головні значення аргументу спряжених комплексних чисел мають одну й ту саму абсолютну величину, але протилежні знаки. Наприклад, головні значення аргументу спряжених чисел – 3 + 3і та – 3 – 3і дорівнюють 135 і – 135.

1.2.10. Тригонометрична форма комплексного числа

Розглянемо трикутник ОАМ (рис. 1.13) і запишемо такі співвідношення між його сторонами:

; .

Звідси , тобто маємо:

; ; ; ; , .

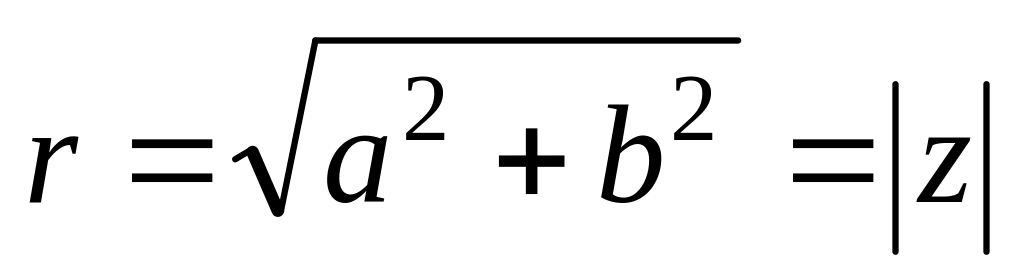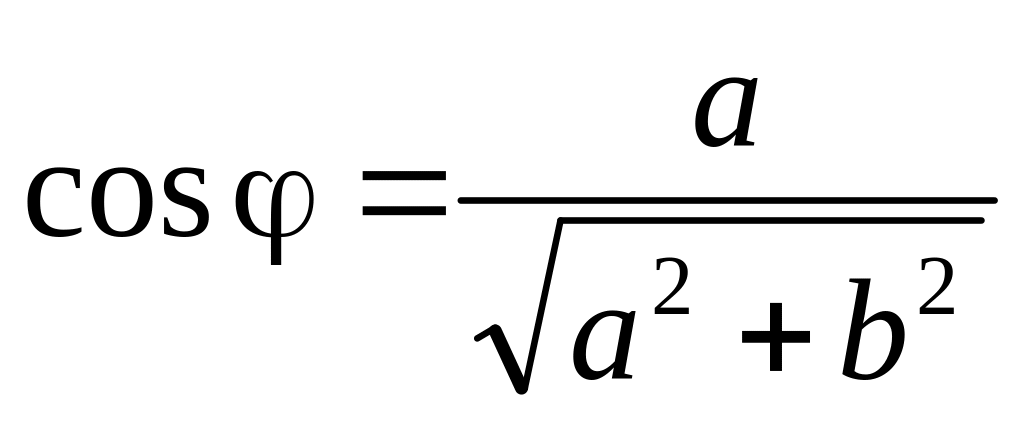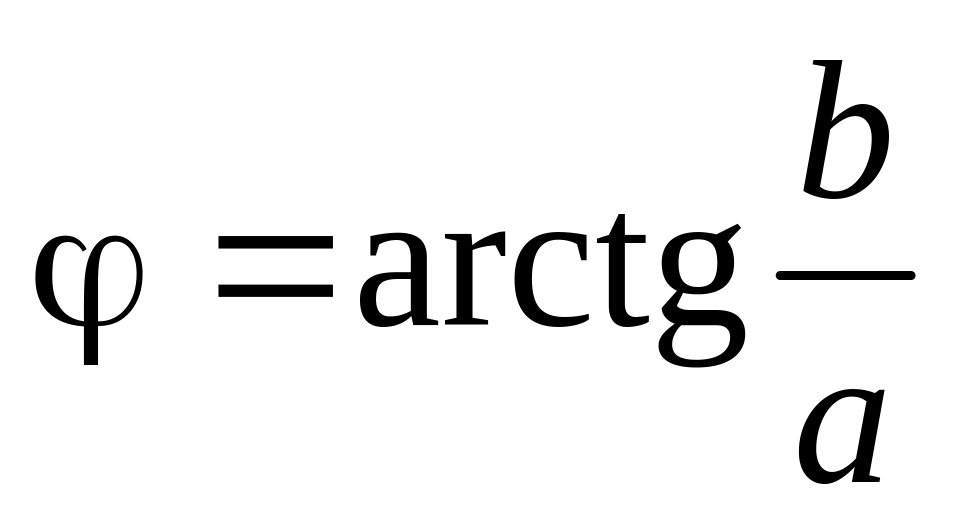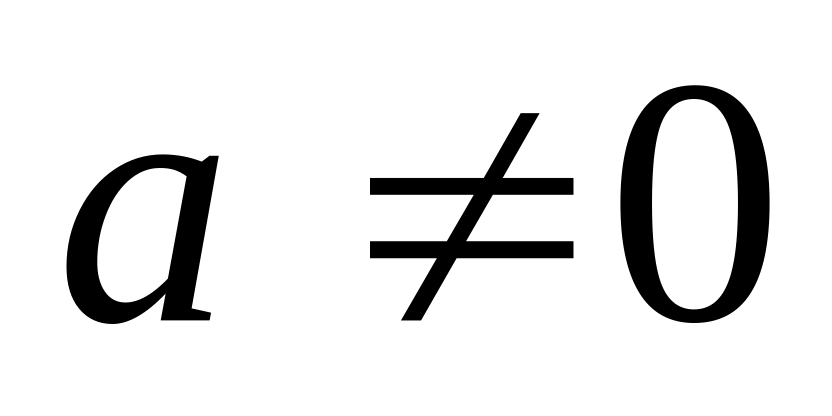(2)

Подання комплексного числа у вигляді (2) називається тригонометричною формою комплексного числа.

З аписати комплексне число 1 + і у тригонометричній формі (рис. 1.15).

 Згідно з (2) маємо:

Рис. 1.15

; . Отже, .

Додавання і віднімання комплексних чисел простіше і зручніше виконувати, коли вони задані в алгебраїчній формі. Для інших алгебраїчних дій зручніша тригонометрична форма.

Наприклад, добуток двох чисел і подається так:

.

24