1.2.4. Дійсні числа

Кожне раціональне число можна подати у вигляді десяткового скінченного або нескінченного періодичного дробу. Наприклад:

4/5 = 0,8; 5/33 = 0,151515… = 0,(15).

І навпаки: кожному нескінченному періодичному дробу відповідає раціональне число. Але є числа, які не можна подати у вигляді скінченного або періодичного дробу.

Означення. Число, яке подається у вигляді нескінченного неперіодичного дробу, називається ірраціональним числом.

— ірраціональне число.

 Розглянемо числа

1; 1,4; 1,414; 1,4142

і їх квадрати

1; 1,96; 1,9881; 1,999396; 1,99996164;

а також числа

2; 1,5; 1,42; 1,4143; 1,41422

і їх квадрати

4; 2,25; 2,0164; 2,00225; 2,00024449.

Очевидно,

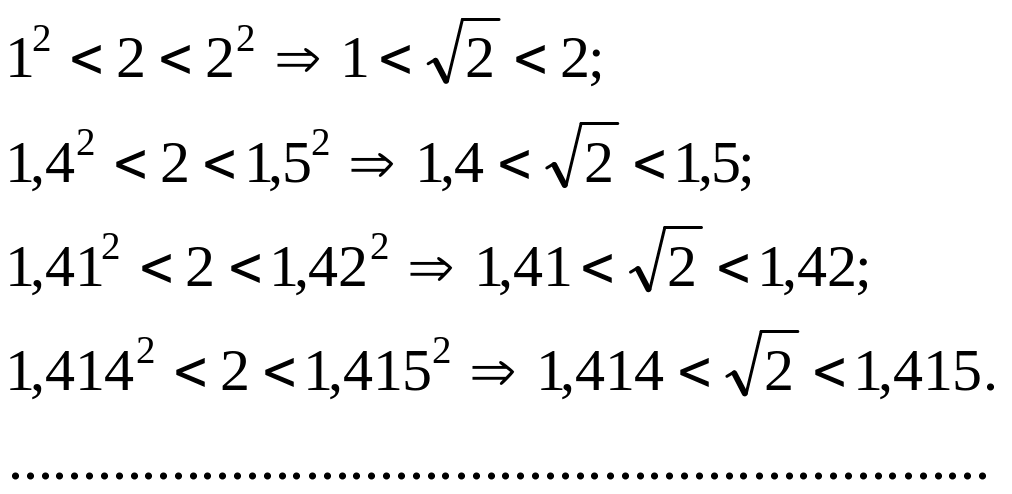
Числа 1; 1,4; 1,41; 1,414; 1,4142; … наближено подають число .

Проте ірраціональні числа утворюються не лише в результаті добування кореня. Наприклад, при порівнянні відрізка, узятого за одиницю, з будь-яким несумірним з ним відрізком дістаємо ірраціональне число. Несумірними відрізками є, скажімо, довжина будь-якого кола та його діаметр. Відношення довжини кола до діаметра дорівнює  = 3,1415926… .

Ірраціональним є також число е = 2,71828… — основа так званих натуральних логарифмів.

На противагу множині раціональних чисел множина ірраціональних чисел не є замкненою відносно дій додавання, віднімання, множення та ділення двох чисел.

Наприклад, числа

0,1010010001… і 0,0101101110… — ірраціональні, але їх сума

0,1010010001…

+

0,0101101110…

_______________

0,11111111111… = 0,(1) = 1/9 — число раціональне.

Сума, різниця, добуток та частка ірраціонального числа і числа раціонального є ірраціональне число. Отже, маючи одне ірраціональне число, за допомогою раціональних чисел можна побудувати множину ірраціональних чисел.

Означення. Множина раціональних чисел разом із множиною ірраціональних чисел утворюють множину дійсних чисел.

З ауваження. Математична строга теорія дійсних чисел була побудована Р. Дедекіндом та Г. Кантором на базі поняття розрізу множини раціональних чисел.

Дійсні числа, як і раціональні, можна зображати на числовій осі. Нехай дано числову вісь із початковою точкою О та одиничним відрізком ОА (рис. 1.9). Зобразимо на цій осі точку, що відповідає ірраціональному числу Для цього на відрізку ОА побудуємо квадрат та його діагональ ОС = Накреслимо коло радіусом ОС. Тоді точка К перетину дуги кола з віссю Ох відповідатиме числу

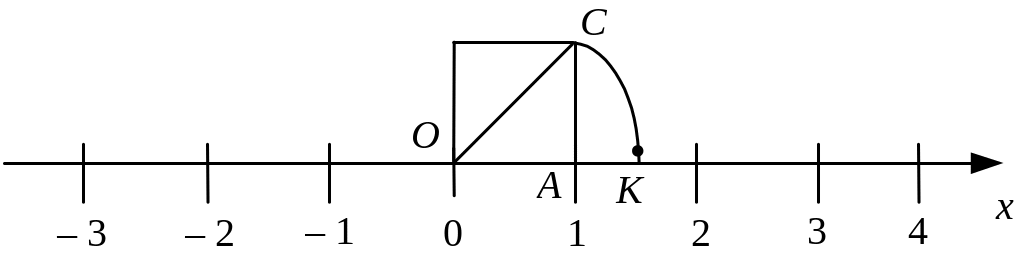
Рис. 1.9

Кожному дійсному числу відповідає єдина точка на числовій осі, та навпаки.

Д овести, що число — ірраціональне.

 Припустимо, що навпаки: — число раціональне, тобто його можна подати у вигляді

,

де m і n — взаємно прості натуральні числа.

Піднесемо обидві частини рівності до квадрата:

, або

Звідси випливає, що числа і m — парні, тобто m = 2k. Тоді pівність можна записати у вигляді

Отже, і n також парні. Це означає, що m і n — парні числа. Але ми припускали, що нескоротний дріб. Здобута суперечність доводить: — iрраціональне число. 

1.2.5. Дії з дійсними числами

Сума, різниця, добуток та частка дійсних чисел є дійсне число.