1.1. Множини

1.1.1. Поняття множини

Поняття множини відіграє велику роль у сучасних математичних дослідженнях. Саме на цьому понятті базуються такі науки, як теорія чисел, математична логіка, дискретна математика та багато інших, причому воно настільки загальне, що дати йому неописове означення, яке б не зводилося до поняття «сукупність» («зібрання», «група» тощо) об’єктів будь-якої природи — елементів множини, дуже важко.

Наведемо класичне тлумачення поняття множини, яке належить одному із засновників теорії множин — Г. Кантору.

Означення. Множину розумітимемо як «сукупність елементів, що тлумачиться та розглядається в цілому».

Це описове означення базується на нематематичному понятті «сукупність» і не є цілком строгим. Усі вимоги щодо строгості задовольняє аксіоматична теорія множин (в якій поняття множини є первісним, неозначуваним) — система правил побудови множин та виконання дій із ними.

Множини позначаються великими латинськими літерами А, В, С, …, Х, У, Z, а елементи множин — малими літерами a, b, c, …, x, y, z. Твердження про те, що елемент а належить множині А, записують у вигляді аА. Коли навпаки — елемент а не належить А, виконують такий запис: аА.

Якщо множина А, утворена з чотирьох елементів а, b, c, d, то записують А = {a, b, c, d}. Множини схематично зображаються колами, прямокутниками.

1 ) Множина простих чисел, менших від 15:

Р = 2, 3, 5, 7, 11, 13.

2) Множина чисел, менших за 15: Р = х  х < 15.

Означення. Порожньою множиною  називається множина, яка не містить жодного елемента (тобто не існує елементів, що мають певну властивість).

Множина натуральних чисел, квадрати яких менші за самі ці числа, є порожня множина Р = n  n² < n, n = 1, 2, 3, ….

Означення. Дві множини А та В називаються рівними, якщо кожний елемент множини А є елементом множини В, і навпаки:

Означення. Множина А, що складається зі скінченної кількості елементів, називається скінченною.

Означення. Число елементів множини називають її потужністю.

Число елементів скінченної множини позначають М (А).

Найчастіше множину задають ознакою, що притаманна всім елементам цієї множини і лише їм.

 х  х²– 5х + 6 = 0 =    х  х — прості числа, менші за 4. Читаємо: «Множина елементів х, які є коренями рівняння х²– 5х + 6 = 0, — це множина з елементів 2, 3». Її ми можемо також уявляти як множину з елементів х, що мають властивість простих чисел, менших за 4.

Означення. Множина А називається підмножиною множини В, якщо кожний елемент множини А є елементом множини В (рис. 1.1):

  : х    х  .

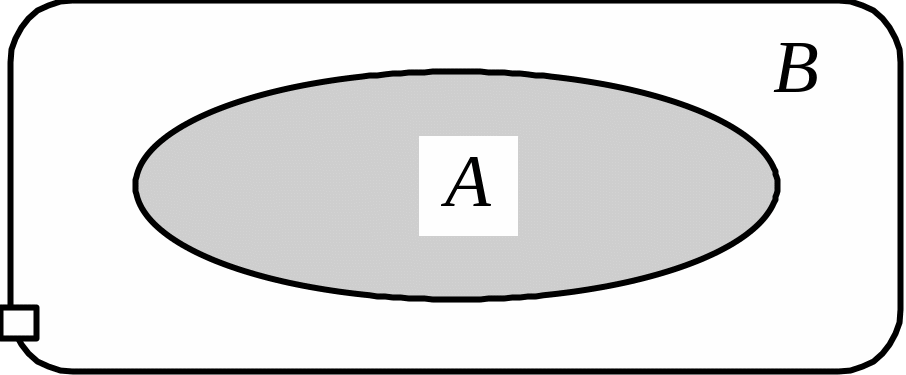
Рис. 1.1

Н ехай маємо множини: П = Православні, Х = Хрис­тияни. Тоді П  Х.

Нехай N = Натуральні числа; Z = {Цілі числа}; Q = {Раціональні числа}; R = {Дійсні числа}; С = {Комплексні числа}. Тоді N  Z  Q  R  C.

1.1.2. Дії з множинами

Означення. Об’єднанням двох множин А та В називається множина , елементи якої належать хоча б одній із цих множин (рис. 1.2):

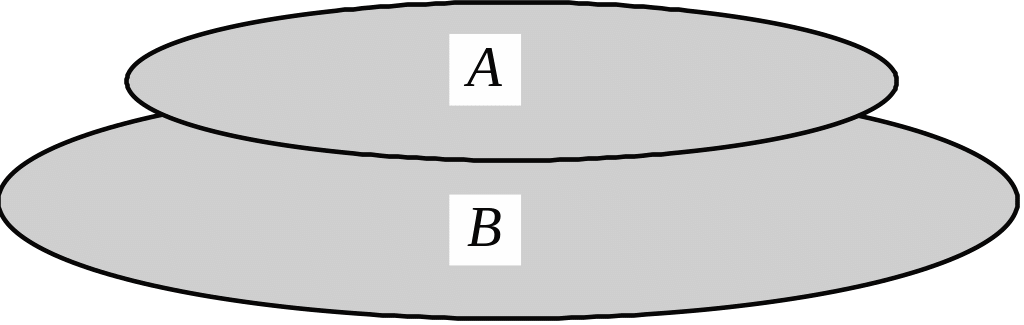
Рис. 1.2

Н ехай А = 1, 2, 3, В = 2, 3, 4, 5. Тоді   = 1, 2, 3, 4, 5.

Якщо А = Раціональні числа, В = Ірраціональні числа, то  Дійсні числа.

Означення. Перерізом двох множин А та В називається множина , елементи якої належать як множині А, так і множині В (рис. 1.3):

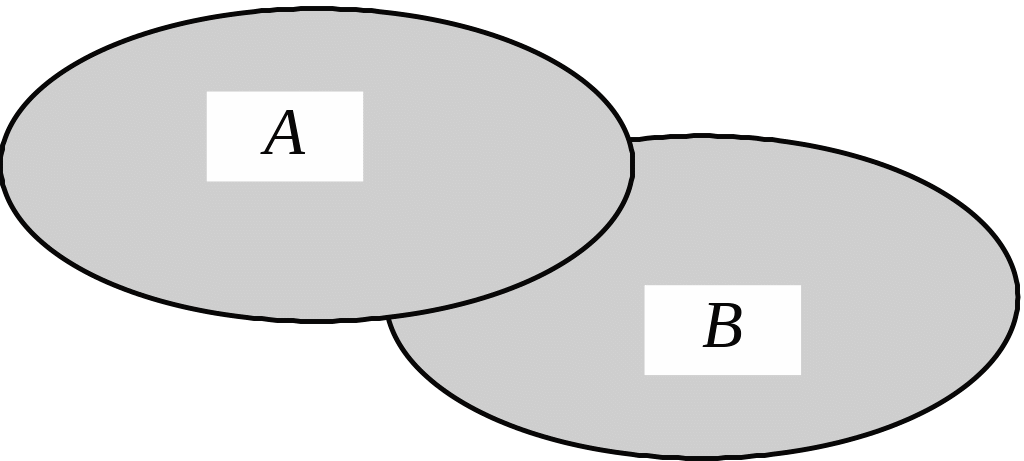
Рис. 1.3

 Парні числа Прості числа = .

Студенти факультету ІСІТ КНЕУ Студенти КНЕУ  Студенти факультету ІСІТ КНЕУ.

Означення. Дві множини А та В називаються неперетинними, якщо (рис. 1.4)

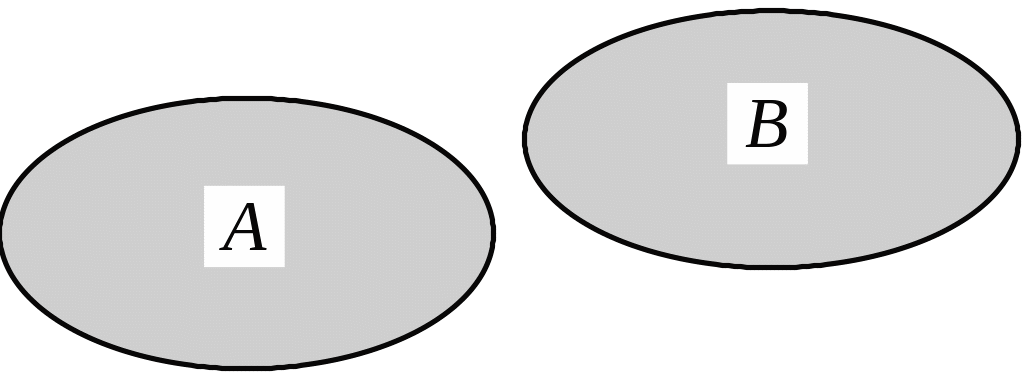
Рис. 1.4

 Раціональні числа Ірраціональні числа  .

Означення. Доповненням множини А до  називається така множина , усі елементи якої належать , але не належать А (рис. 1.5):

.

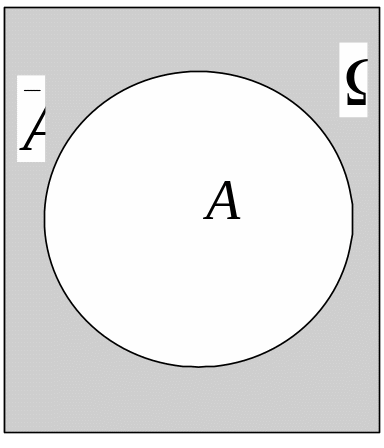
Рис. 1.5

Я кщо Q  Раціональні числа   R = {Дійсні числа}, то   Ірраціональні числа.

Нехай   Люди, М  Особи чоловічої статі. Тоді  = Особи жіночої статі.

Означення. Множини А_і (і = 1, 2, …, п) утворюють розбиття (на класи) множини , якщо їх об’єднання становить  і вони є попарно неперетинними (рис. 1.6):

1)  = ; 2)  = , і  j.

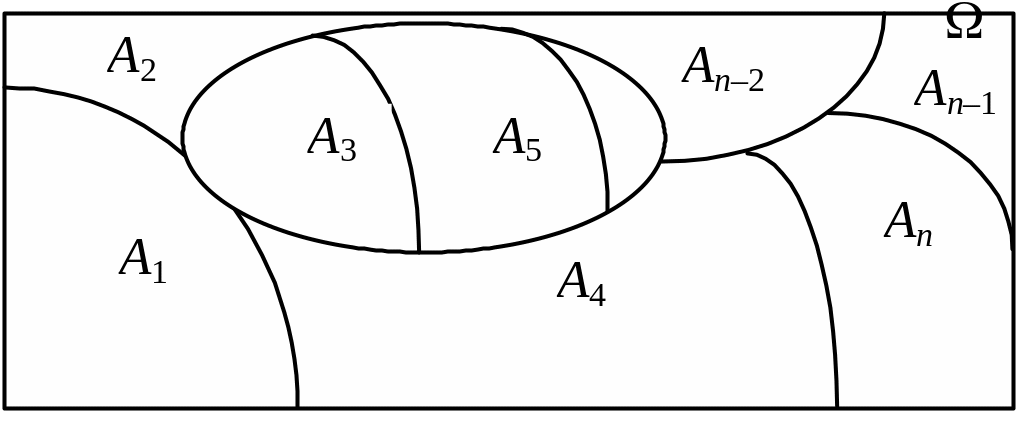
Рис. 1.6

Н ехай   Студенти дев’яти факультетів КНЕУ. Позначимо: = Студенти і-го факультету КНЕУ (і = 1, 2, 3, …, 9). Тоді

Лема. Для будь-яких скінченних множин А та В виконується рівність

.

Доведення. 1. Нехай множини А та В не перетинаються, тобто . Тоді , оскільки об’єд­нання розглядуваних множин утворюється додаванням усіх елементів однієї множини до елементів іншої.

2. Якщо множини А та В перетинаються, то кількість їх спільних елементів дорівнює  Об’єднання множин А та В утворюється з елементів множини А та елементів множини В, що не є елементами множини А. Число таких елементів становить . Отже,

. 

І спит з математики складали 250 абітурієнтів. Оцінку, нижчу за «відмінно», дістали 180 з них, а витримали іспит 210 абітурієнтів. Скільки абітурієнтів склали іспит на «добре» та «задовільно»?

 Нехай А — множина абітурієнтів, які витримали іспит; В — множина абітурієнтів, оцінка яких нижча за «відмінно». Тоді за умовою маємо:

.

Отже, абітурієнти, котрі отримали оцінки «задовільно» й «добре», становлять множину . Згідно з лемою знаходимо:

. 