Свойства определенного интеграла.

1. Определенный интеграл от суммы конечного числа функций fi(x), f₂(x),... ,f_n(x), заданных на отрезке [а, Ь], равен сумме определенных интегралов от слагаемых функций:

2. Постоянный множитель к подынтегральной функции можно выносить за знак определенного интеграла

3. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл сохранит абсолютную величину и изменит свой знак на противоположный:

4. Если пределы интегрирования равны между собой, то определенный интеграл равен нулю:

7. Связь между определенным и неопределенным интегралами. Формула Ньютона - Лейбница.

Общность обозначения определенного неопределенного интегралов подчеркивает тесную связь между ними, хотя определенный интеграл есть число, а неопределенный интеграл - совокупность первообразных функций. Связь между определенным и неопределенным интегралами устанавливает формула Ньютона - Лейбница.

Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования. Вертикальная черта с верхним и нижним пределами, стоящая справа от символа функции F(x), называется знаком двойной подстановки.

Методы вычисления определенного интеграла:

1. метод подстановки или замены переменной

2. метод интегрирования по частям

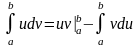
3. приближенные методы вычисления определенного интеграла

   1. формула прямоугольников

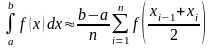
   2. формула трапеции

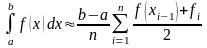
Площадь криволинейной трапеции, ограниченной у = f(х) [ f(х)≥0], прямыми х = а, х = b и отрезком [а,b] оси Oх, вычисляется по формуле

Площадь фигуры, ограниченной кривыми у = f(х) и у = g(х) [ g(х)≤ f(х)], прямыми х = а, х = b вычисляется по формуле

Для вычисления фигур более сложной формы используют разбиение фигуры на более простые элементы и площадь фигуры находят сложением площадей.

Пример: Вычислить площадь фигуры, ограниченной линиями у=4-х², у=0. Площадь фигуры:

Если кривая задана параметрическими уравнениями х = х(t), у = у (t), то площадь криволинейной трапеции, ограниченной этой кривой, прямыми х = а, х = b и отрезком [а,b]оси Ох, выражается формулой

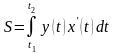
где t₁ и t₂ определяются из уравнений а = х(t₁), b = х(t₂) [ y(t)≥0 при t₁<t<t₂].

Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(Ө) и двумя полярными радиусами, находятся по формуле

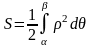
Вычисление объема тела по известным площадям поперечных сечений.

Если площадь сечения тела плоскостьб, перпендикулярной оси Ох, выражена как функция от х , т.е. в виде S = S(х) (а<x<b), то объем части тела, заключенной между перпендикулярными оси Ох плоскостями х = а и х = b находят по формуле

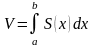
Вычисление объема тела вращения

Если криволинейная трапеция, ограниченная кривой у = f(x) и прямыми х = а, х = b, у = 0, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле

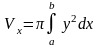
Если фигура, ограниченная кривыми у₁ = f₁(x) и у₂ = f₂(x) [0≤f₁≤f₂] и прямыми х = а, х = b, вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле