Статистическая совокупность, её элементы, признаки.

Статистическая совокупность – группа, состоящая из множества относительно однородных элементов (единиц наблюдения). Например, группа оперированных , население на участке, больные стационара, новорожденные на данном участке, пациенты поликлиники, больные на дому и т.д..

Единица наблюдения – каждое отдельное явление, подлежащее учету, наделенное признаками сходства.

В большинстве социально- гигиенических исследований учитываемыми признаками является: пол, возраст, семейное положение, уровень образования, доход и размеры жилплощади на одного человека, масса тела, рост, длительность пребывания в стационаре и др. (количественные признаки, выраженные числом).

Различают так же факторные и результативные признаки в зависимости от характера влияния: какой признак на какой влияет (возраст – факторный признак, а рост - результативный).

Методами обработки медико – биолоических исследований являются методы расчета средних, относительных величин.

Одной из основных областей применения математической статистики в медицине является обоснование выводов, вытекающих из сравнения статистических показателей. Основным вопросом при этом является суждение о том, в какой мере обнаружения при исследовании разность между выборочными показателями может свидетельствовать о существенном, неслучайном различии генеральных совокупностей.

В статистике широкое применение нашла нулевая гипотеза Н₀. Так если одна выборка извлечена из генеральной совокупности с параметрами М(х) и σ_х, а другая – из совокупностей с параметрами М(Y) и σ_у, то нулевая гипотеза исходит из того, что М(х) – М(Y) = 0 и σ_х - σ_у = 0 (отсюда и название гипотезы – нулевая).

Противоположная нулевой – конкурирующая гипотеза Н₁ – исходит из предположения, что М(х) – М(Y) ≠ 0 и σ_х - σ_у ≠ 0.

Для проверки принятой гипотезы используют величины, функции распределения которых известны и сведены в специальные таблицы. Принимают три уровня значимости, или вероятности ошибки, допускаемой при проверке статистических гипотез:

5% -ный (вероятность ошибочной оценки Р = 0,05)

1% -ный (Р = 0,01)

0,1% ный (Р = 0,001).

В биологических исследованиях часто считают достаточным 5% -ный уровень значимости. При этом гипотезу Н₀ не отвергают, если вероятность ошибочности оценки относительно принятой гипотезы превышает 5%.

Если же эта вероятность меньше 5 %, то принятую гипотезу следует отвергнуть на взятом уровне. Ошибка при этом возможна не более, чем в 5 % случаев, т.е. она маловероятна. При более ответственных исследованиях уровень значимости может быть уменьшен до 1 % или даже 0,1 %.

В области биометрии применяются два вида статистических критериев.

Параметрические, построенные на основании параметров данной совокупности и представляющие функции этих параметров.

Непараметрические - представляющие собой функции, зависящие непосредственно от варианта данной совокупности с их частотами.

Параметрические критерии.

Метод Стьюдента используют для сравнительной оценки средних величин. Он позволяет судить на основании экспериментальных данных о равенстве или неравенстве двух средних нормальных совокупностей и используется при условии, что:

1. Изучаемые совокупности распределены по нормальному закону.

2. Генеральные дисперсии одинаковы.

Этапы применения методов.

1. Из опытных данных следует вычислить так называемое фактическое значение критерия t_ср.

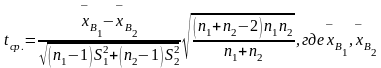- среднее выборочное для первой и второй совокупности; - исправленные выборочные дисперсии для первой и второй совокупности; n₁ и n₂ – число значений исследуемой в первой и второй совокупностях.

2. следует найти табличное значение критерия t_st. Эта величина зависит от значения параметров k = n₁ + n₂ -2 и а – уровень значимости.

3. следует сравнить абсолютное значение t_ф с t_st. Если 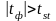нет оснований утверждать, что генеральные средние различны, если , различие между генеральными средними существенно.

В медицине часто приходится подвергать анализу явления, распределения которых отличаются от нормального (оценить вкусовые качества пищевых продуктов, лекарственных препаратов). В таких случаях используют непараметрические критерии.

Критерии знаков.

При использовании этого критерия учитывается не абсолютная величина различий, а направленность сравниваемых парных наблюдений, которая обычно обозначается знаками.

Методика применения знаков:

1. определяется направленность различий сравниваемых парных наблюдений, результаты обозначаются знаками «+» и «-»; варианты, не имеющие изменений, из дальнейшей оценки исключаются;

2. подсчитывается общее число n парных наблюдений, имеющих различия(т.е. отмеченных знаками «+» и «-»);

3. подсчитывается число знаков Z_ф чаще всего встречающихся;

4. полученное число Z_ф сравнивается (с учетом n) с критическими значениями Z_st, содержащимися в таблице.

Если Z_ф≤ Z_st, то принимается нулевая гипотеза.

Если Z_ф> Z_st, то различия могут считаться значимыми с соответствующими уровнями значимости(α<0.05,α<0.01).

Критерий Ван дер Вардена обладает большей статистической мощностью, чем критерий знаков. Его применяют для проверки нулевой гипотезы при сравнении друг с другом независимых выборок.

Методика критерия:

1. сравниваемые выборки ранжируют в один общий ряд по возрастающим значениям признака.

2. каждому члену ряда присваивается порядковый номер, отмечающий его место в общем ранжированном строю.

3. по порядковым номерам одной из выборок, обычно меньше по объему, находят отношение , т.е сумма всех членов сравниваемых групп, увеличенная на 1; R – порядковый номер членов ряда, их «ранг».

4. с помощью специальной таблицы находят значения функции 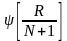, для каждого значения .

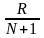5. суммируя результаты(обязательно с учетом знаков), получают величину

Х_ф =

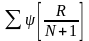
6. сравнивают Х_ф с критической точкой этого критерия Х_stдля принятого уровня значимости р и общего числа членов сравниваемых выборок N = n₁ + n₂. нулевая гипотеза сводится к предположению, что сравниваемые выборки извлечены из генеральных совокупностей с одинаковыми функциями распределения. Если окажется, что Х_ф≥Х_st, нулевая гипотеза должна быть отвергнута на принятом уровне значимости.