Теорема умножения вероятностей:

События А и В называются независимыми, если вероятность появления события А не зависит от того, произошло событие В или нет, и наоборот, вероятность появления события В не зависит от того, произошло событие А или нет.

Вероятность совместного появления независимых событий равна произведению их вероятностей. Для двух событий Р(А и В)=Р(А)·Р(В).

Пример: В одной урне 5 черных и 10 белых шаров, в другой 3 черных и 17 белых. Найти вероятность того, что при первом вынимании шаров из каждой урны оба шара окажутся черными.

Решение: вероятность вытаскивания черного шара из первой урны (событие А) – Р(А) = 5/15 = 1/3, черного шара из второй урны (событие В) – Р(В) = 3/20

Р(А и В)=Р(А)·Р(В) = (1/3)(3/20) = 3/60 = 1/20.

На практике нередко вероятность события В зависит оттого, произошло некоторое другое событие А или нет. В этом случае говорят об условной вероятности, т.е. вероятности события В при условии, что событие А произошло. Условную вероятность обозначают P(B/A).

Теорема умножения вероятностей усложняется, если определяется вероятность события, состоящего из совместного появления двух зависимых между собой событий. В том случае, когда событие В выполняется при условии, что событие А имело место, вероятность совместного появления двух этих событий равна

Р(А и В)=Р(А)Р(В/А).

В урне 5 шаров: 3 белых и 2 черных. Найти вероятность того, что последовательно один за другим будут вынуты черный и белый шары.

Вероятность того, что первым будет изъят черный шар (событие А), равна Р(А) = m/n = 2/5. После удаления черного шара в урне остается 4 шара: 3 белых и 1 черный. В этом случае вероятность вынимания белого шара (событие В после выполнения события А) равна Р(В/А) = ¾. Получаем Р(А и В)=Р(А)Р(В/А) = (2/5)(3/4) = 3/10.

Если событие А может произойти только с одним из событий Н₁,Н₂,…Н_n, которые образуют полную систему попарно несовместных событий, то вероятность события А определяется по формуле полной вероятности

Р(А) = Р(А/Н₁)Р(Н₁)+Р(А/Н₂)Р(H₂)+...+Р(А/Н_n)Р(Н_n).

Для вычисления вероятности P(H_i /A) в этом случае используется формула Байесa:

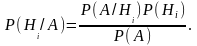
Контрольные вопросы

1. Дайте определение вероятности событий.

2. Какие события называются равновозможными?

3. Какие события называются достоверными?

4. Какие события называются невозможными?

5. Какие события называются противоположными?

6. Сформулируйте классическое определение вероятности.

7. Чему равна вероятность достоверного события? Невозможного события?

8. Назовите формулы сложения и умножения вероятностей.

Домашнее задание

Заполните в рабочей тетради занятие 11-12.

Лекция № 6

Тема: : Основные понятия теории вероятности и математической статистики

План:

2. Случайные величины.

3. Дисперсия случайной величины.

Цели: создание благоприятных условий для введения понятия случайных событий;

познакомить с законом распределения случайных величин; познакомить с важными характеристиками случайных величин: математическое ожидание, дисперсия, среднее квадратичное отклонение.