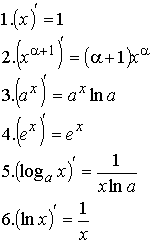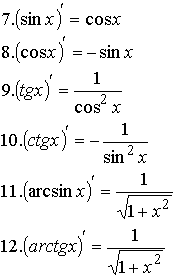Лекции по предмету «Математика» для студентов, обучающихся по специальности «Сестринское дело»
-
Номера занятий
Наименование разделов и тем
Количество часов
Лекции
1
Дифференциальное исчисление.
2
2
Дифференциальное исчисление.
2
3
Интегральное исчисление.
Последовательности пределы и ряды
1
1
4
Последовательности пределы и ряды. Операции с множествами. Основные понятия теории графов. Комбинаторика.
1
1
5
Основные понятия теории вероятности и математической статистики.
2
6
Основные понятия теории вероятности и математической статистики.
2
7
Математическая статистика и её роль в медицине и здравоохранении.
2
8
Численные методы математической подготовки среднего медицинского персонала.
Решение прикладных задач в области профессиональной деятельности
1
1
Лекция № 1
Тема: Дифференциальное исчисление
План:
Производная функции, её геометрический и механический смысл.
Формулы производных.
Изучение производных суммы, произведения, частного функций.
Обоснование производных элементарных и сложных функций, обратных функций
Цели: создание благоприятных условий для изучения понятия производная функции, ее геометрического и механического смысла; познакомить с формулами нахождения производных; изучения правил нахождения производных; производная сложных и обратных функций.
1. Приращение аргумента и функции.
Пусть функция f(x) определена на некотором интервале I, х0 и х два произвольных значения аргумента из этого интервала. Разность между двумя значениями аргумента называется приращением аргумента и обозначают Δх:
х - х0 =Δх, откуда х = х0 + Δх, т.е. значение аргумента х можно определить через х0 и его же приращение Д х.
Разность между двумя значениями функции называется приращением функции и обозначают Δу: Δу=Δ f=f(xo+ Δx)-f(xo)
Как видно из рисунка приращение аргументаΔ х, изображается приращением абсциссы точки графика функции у = f(x), а приращение функции Δf - приращением ординаты этой точки.
2. Определение производной.
Пусть функция y = f(x) определена в промежутке X.
Предел отношения приращения функции Δf к приращению аргумента Δх, когда Δх стремится к нулю, при условии, что этот предел существует, называется производной функции f(x) в точке х.
Или :
Производной функции y = f(x) в точке хo называется предел
=
.
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке xo; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен+ ∞ (или - ∞), то при условии, что функция в точке хo непрерывна, будем говорить, что функция f(x) имеет в точке хo бесконечную производную.
Производная
обозначается символами y/(x0),
f/(x0)
;
,
.
Читается f'(x) (эф штрих от икс).
Нахождение производной называется дифференцированием функции, поэтому выражение "продифференцировать функцию" равносильно выражению "найти производную функции".
3. Физический смысл производной.
Исходя из определения производной, можно сказать:
мгновенная скорость прямолинейного движения есть производная от пути S по времени t: v (t)= S'(t);
мгновенная скорость химической реакции есть производная от функции X по аргументу t: v (t) = x'(t).
Таким образом, можно сделать вывод: производная функции у = f(x) по аргументу х есть мгновенная скорость изменения функции у = f(x). В этом состоит физический смысл производной.
Вторая производная функции у = f(x) по аргументу х есть ускорение изменения функции у = f(x).
4. Геометрический, смысл производной.
Рассмотрим график функции f(x) и построим на этом графике произвольным образом точку М. В данной точке М проведем касательную к графику функции f(x)
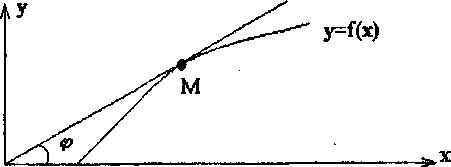
Итак, угловой коэффициент касательной к графику функции в данной точке равен значению ее производной в точке касания. В этом состоит геометрический смысл производной.
k = tga = f'(x0)
Таблица производных
|
|
