МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БРЕСТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра сопротивления материалов и теоретической механики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ №1, №2

по курсу «Сопротивление материалов»

ДЛЯ СТУДЕНТОВ СПЕЦИАЛЬНОСТИ 1-70 04 03

«Водоснабжение, водоотведение и охрана водных ресурсов»

Специализация 1-70 03 01 «Системы водоснабжения и водоотведения»

ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

Брест 2012

УДК 539.3/8

Сопротивление материалов является одной из общепрофессиональных дисциплин при подготовке инженеров.

Для приобретения навыков инженерных расчётов студентами выполняются контрольные работы по основным разделам курса.

В данных методических указаниях кратко излагается теоретический материал основных разделов курса сопротивления материалов, даны примеры расчётов и приведены задания по выполнению контрольных работ.

Составители: Дерещук Е.М., к.т.н., доцент

Хвисевич В.М., к.т.н., доцент

Рецензенты:

Учреждение образования

© «Брестский государственный технический университет», 2012

ПРАВИЛА ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

1. Первой страницей контрольной работы является её титульный лист установленной формы «Приложение 1».

2. Текстовая часть выполняется рукописным способом чернилами, чётким почерком, на одной стороне белой бумаги формата А4 (210×297). Лист обрамляется рамкой. Линия поля слева проходит на расстоянии 20 мм от края листа (для подшивки) и 5 мм сверху, справа и снизу. В правом нижнем углу в рамке указывается номер листа (см. «Приложение 2»). Титульный лист включается в сквозную нумерацию страниц, но на нём номер 1 не ставится. Листы нумеруются арабскими цифрами.

3. Перед решением задачи надо написать полностью её условие с числовыми данными, которые выбираются из соответствующих таблиц согласно шифру, выданного преподавателем и первым четырём буквам русского алфавита.

Например, Задача № «х»

шифр – 1 4 2 6

буквы – а б в г

Согласно буквам, из указанной таблицы выбирают число, которое находится на пересечении соответствующей строки и столбца.

Причём, вначале по букве определяется число строки, а затем в столбце находится искомая цифра.

4. К решению задач рекомендуется приступать лишь после предварительного изучения соответствующего курса по сопротивлению материалов иначе могут возникнуть большие затруднения при выполнении контрольных работ.

5. Студент должен знать, что язык техники – формула и чертёж. Поэтому необходимо на миллиметровке аккуратно в масштабе вычертить расчётную схему с указанием всех числовых данных, приложенных сил и размеров, необходимых для расчёта.

6. При выполнении расчётов сначала записывается формула, затем вместо каждой значащей буквы подставляется её числовая величина. Значения, полученных расчётных величин, следует округлять до необходимой точности. В конце результата обязательно указывать размерность всех величин.

7. Эпюры усилий, напряжений, перемещений и т.д. необходимо строить на одном листе с расчётной схемой. При этом в характерных сечениях, точках указываются значения ординат.

8. Все рисунки и схемы должны быть пронумерованы, обозначены, упомянуты в листе с соответствующими ссылками.

9. Студент не позже 10-ти дневного срока до начала сессии представляет в деканат контрольную работу на проверку.

10. Правильно выполненная контрольная работа допускается к защите. Защищая контрольную работу, студент должен уметь ответить на вопросы, связанные с её выполнением, а также уметь решать задачи по её тематике.

11. По требованию рецензента при возвращении контрольной работы на доработку или для исправления ошибок студент в кратчайший срок должен на отдельных листах исправить ошибки, выполнить все указания и вложить листы в соответствующие места рецензированной работы. Все исправления, в ранее выполненной работе, не допускаются.

12. Каждая контрольная работа отдельно сшивается, листы в «файлы» не вставляются.

13. Работы, выполненные с нарушением этих указаний, не рассматриваются.

1. Центральное растяжение и сжатие статически определимого прямого ступенчатого бруса

Под растяжением или сжатием понимается такой вид нагружения стержня (бруса), при котором возникают внутренние продольные силы, направленные вдоль его продольной оси.

Значение продольной силы в любой отсечённой части стержня находится методом сечений на основе уравнений статики из условия равновесия этой части стержня.

Определив величину продольных сил от внешних нагрузок в характерных сечениях, строим эпюру распределения этих сил по длине стержня.

Далее по формуле определяем напряжения в характерных сечениях и строим эпюру распределения нормальных напряжений по длине стержня.

Под влиянием внешних нагрузок стержень изменяет свою первоначальную длину. Все сечения на отдельных участках перемещаются относительно продольной оси в ту или иную сторону в зависимости от того, происходит растяжение или сжатие стержня на участке. Перемещение граничного сечения каждого (i-го) участка характеризуется абсолютной деформацией , где - первоначальная длина участка стержня, - конечная длина участка стержня после приложения нагрузки. Полное удлинение или укорочение ступенчатого стержня, если в пределах участка E, N и А не изменяются, определяется алгебраическим суммированием удлинений (укорочений) всех его участков по формулам:

или

Если, например, N и А переменны по длине участков, то полное перемещение стержня определяется по формуле:

Интегрирование выполняется в пределах каждого участка. Затем удлинения или укорочения каждого участка суммируются со своим знаком.

Если абсолютную деформацию стержня отнести к его первоначальной длине, получим относительную деформацию , которая не зависит от первоначальной длины стержня. Следовательно, по ней можно судить о материале из которого изготовлен стержень.

Центрально сжатые или растянутые стержни испытывают, помимо продольных деформаций и поперечные деформации, определяемые следующим образом:

, где - ширина стержня до деформации, - ширина стержня после деформации, тогда относительная поперечная деформация .

Отношение относительных величин поперечной к продольной деформации называют коэффициентом Пуассона.

.

Значение этого коэффициента для различных изотропных материалов изменяется в пределах .

Зная величину коэффициента Пуассона, можно вычислить абсолютное и относительное изменение объёма стержня.

Задача 1

Расчёт статически определимого ступенчатого бруса

Дано: ступенчатый брус (выбранный согласно шифру из таблицы 1.1, по рисунку 1.1) загружен осевыми нагрузками.

Требуется:

1) построить эпюру продольных сил (N);

2) построить эпюру нормальных напряжений ( );

3) построить эпюру перемещений ( );

4) произвести проверку прочности и жёсткости бруса.

Пример расчёта статически определимого ступенчатого бруса

Дано: F = 100кН; q = 50кН/м; = 40 см; = 50 см; = 60 см; = 4 см²;

= 8 см²; =12 см²; R = 210МПа; Е = 2 · 10⁵МПа;

Основой для расчёта является правильно выполненная расчётная схема. Поэтому предлагается последовательность её составления и только потом следует приступать к расчёту:

1) расчётная схема изображается в масштабе на миллиметровке;

2) на ней проставляются в числовом выражении размеры длин участков, площадей, величина приложенных сил;

3) брус разбивается на участки (1, 2, 3), границы которых отмечаются прописными буквами (а, б, в, г, d…);

4) для выделенного сечения на участке, записывается аналитическое выражение для нормальной силы «N», используя метод сечений;

5) вычисляются значения «N» на границах участка;

6) строится эпюра «N» с указанием масштаба и в характерных сечениях проставляются значения внутренних продольных сил;

7) затем строятся эпюры напряжения и перемещения .

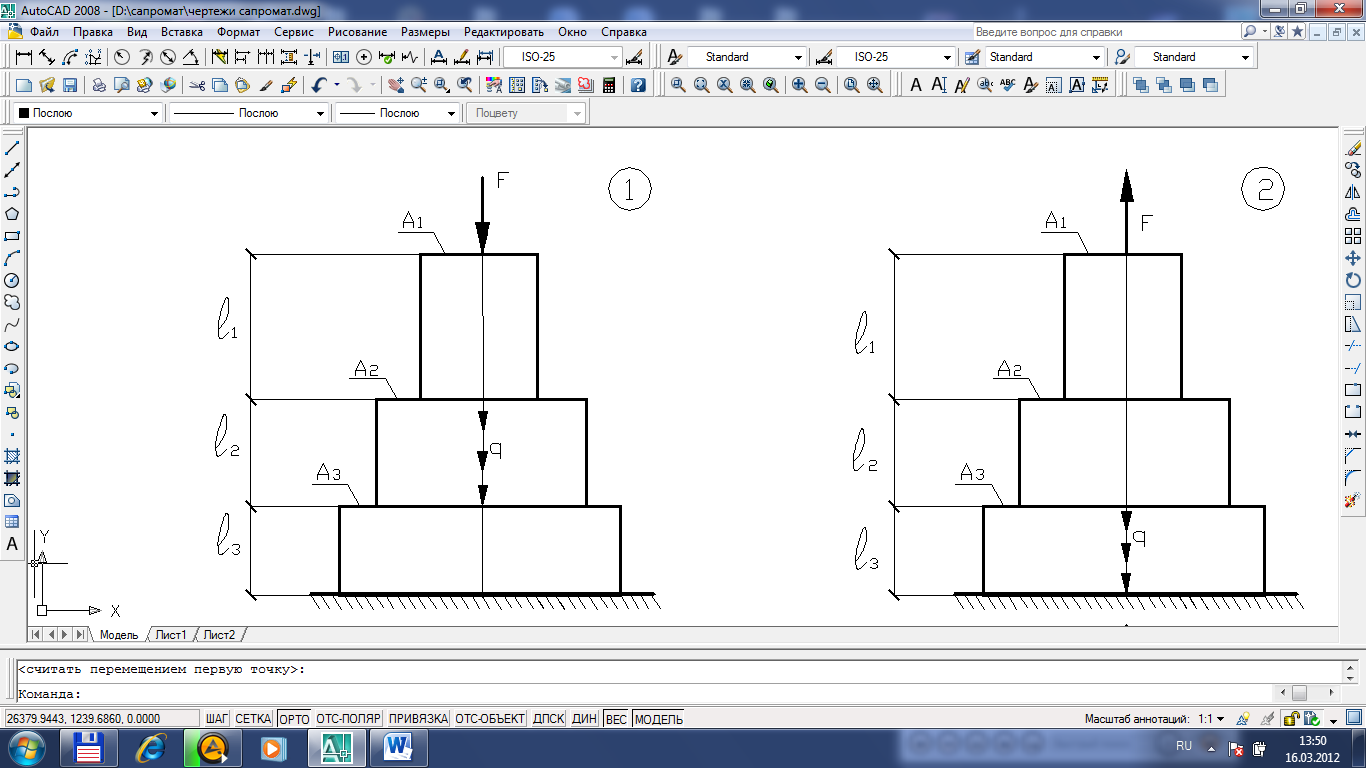
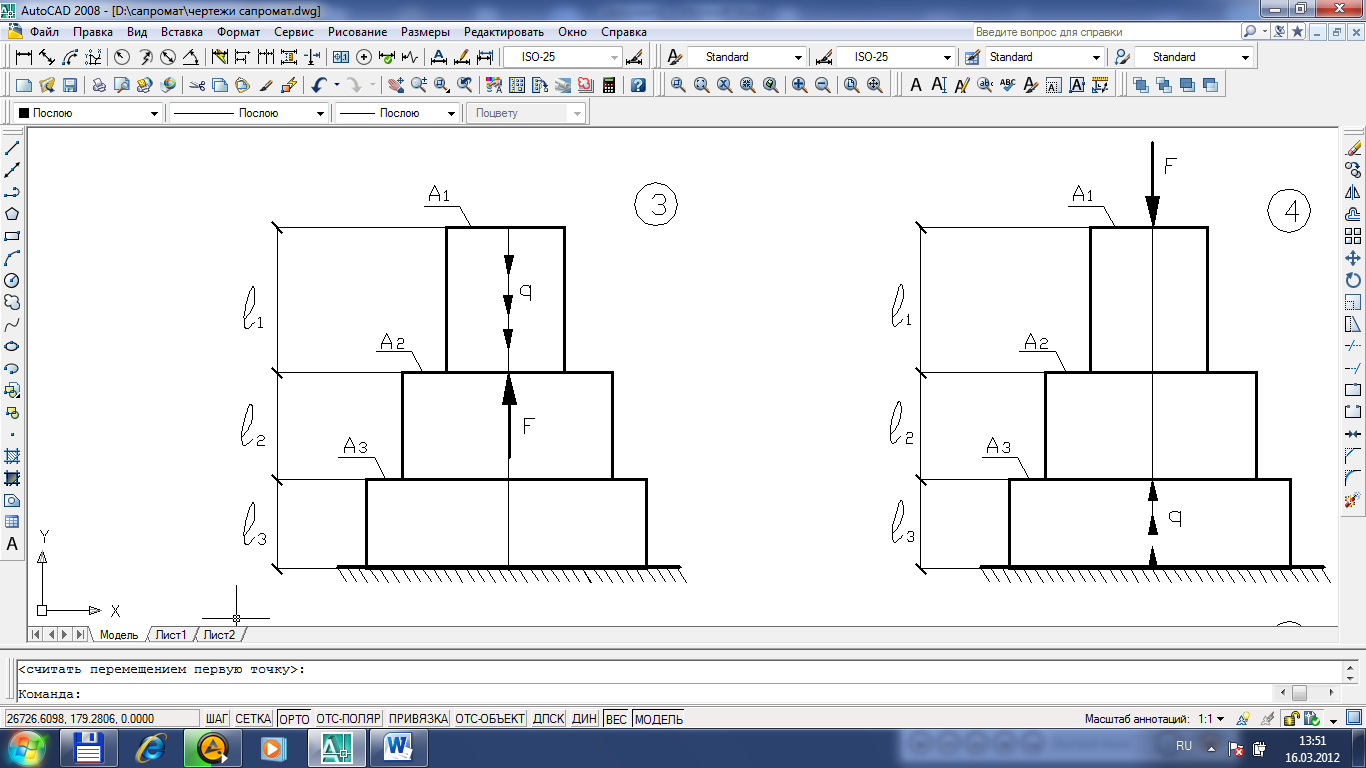
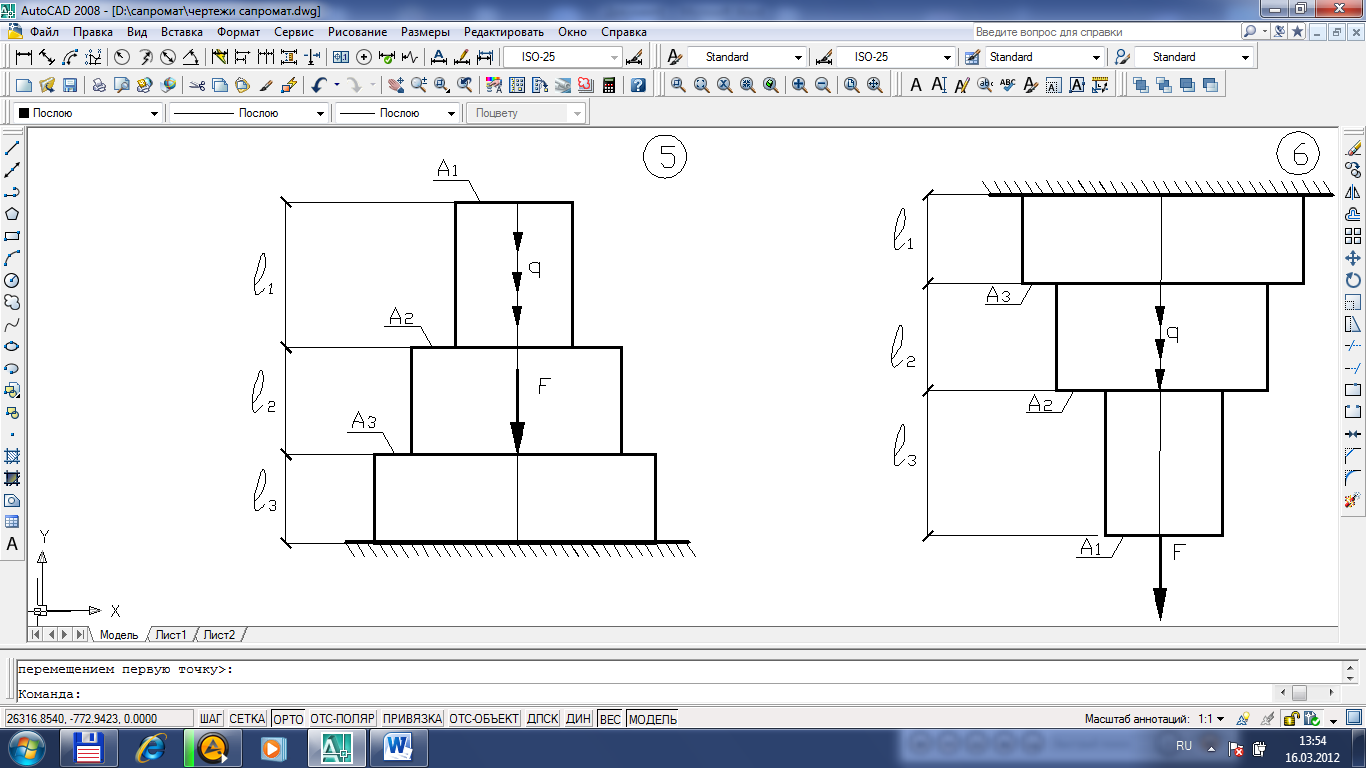
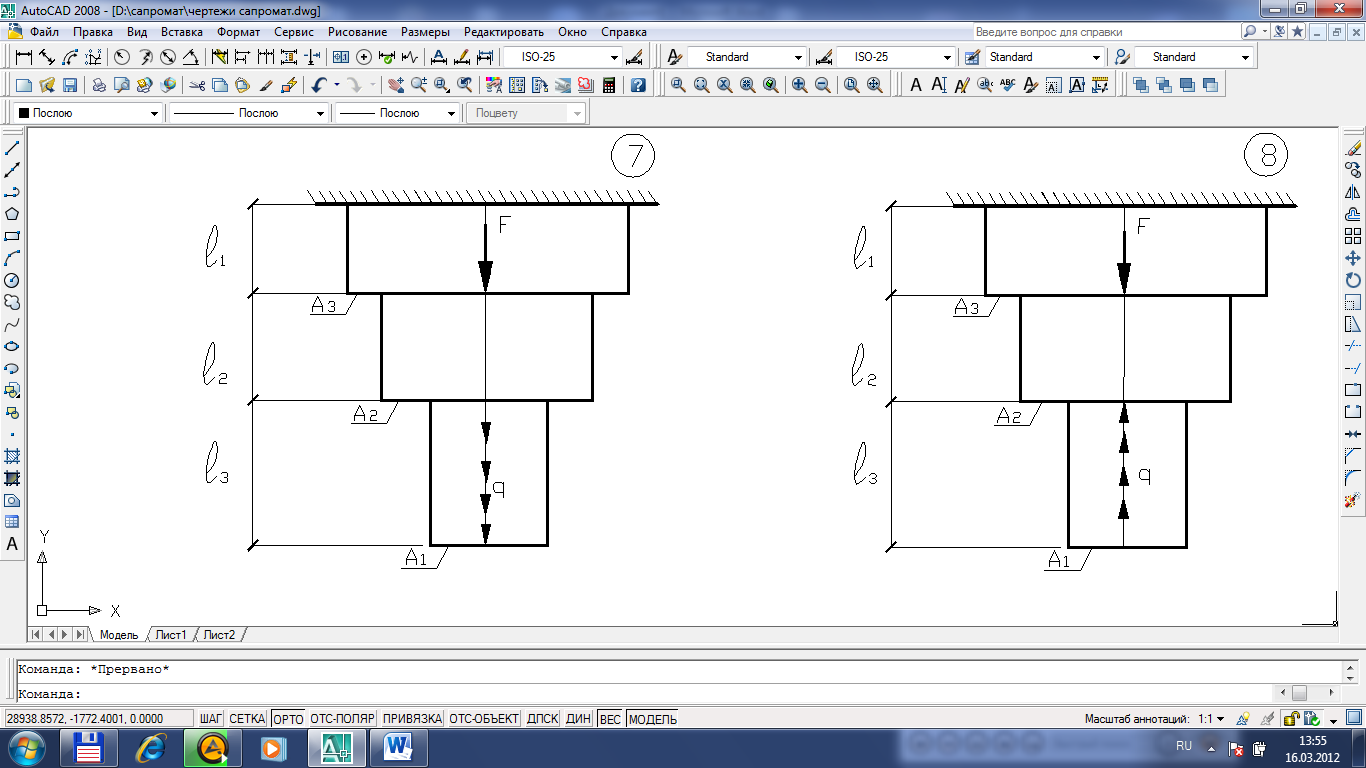
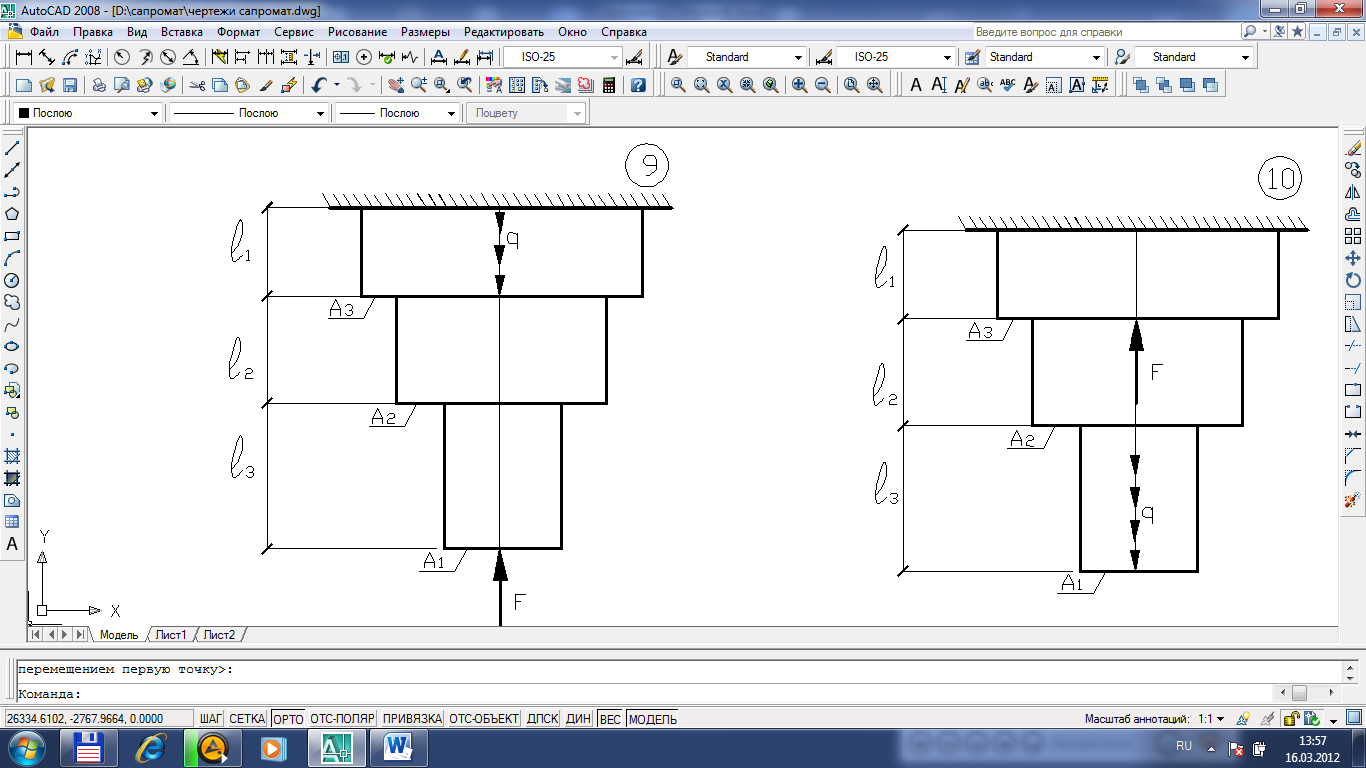
Рисунок 1.1 – Схемы ступенчатых брусьев

Таблица 1.1

Числовые параметры к ступенчатым брусьям.

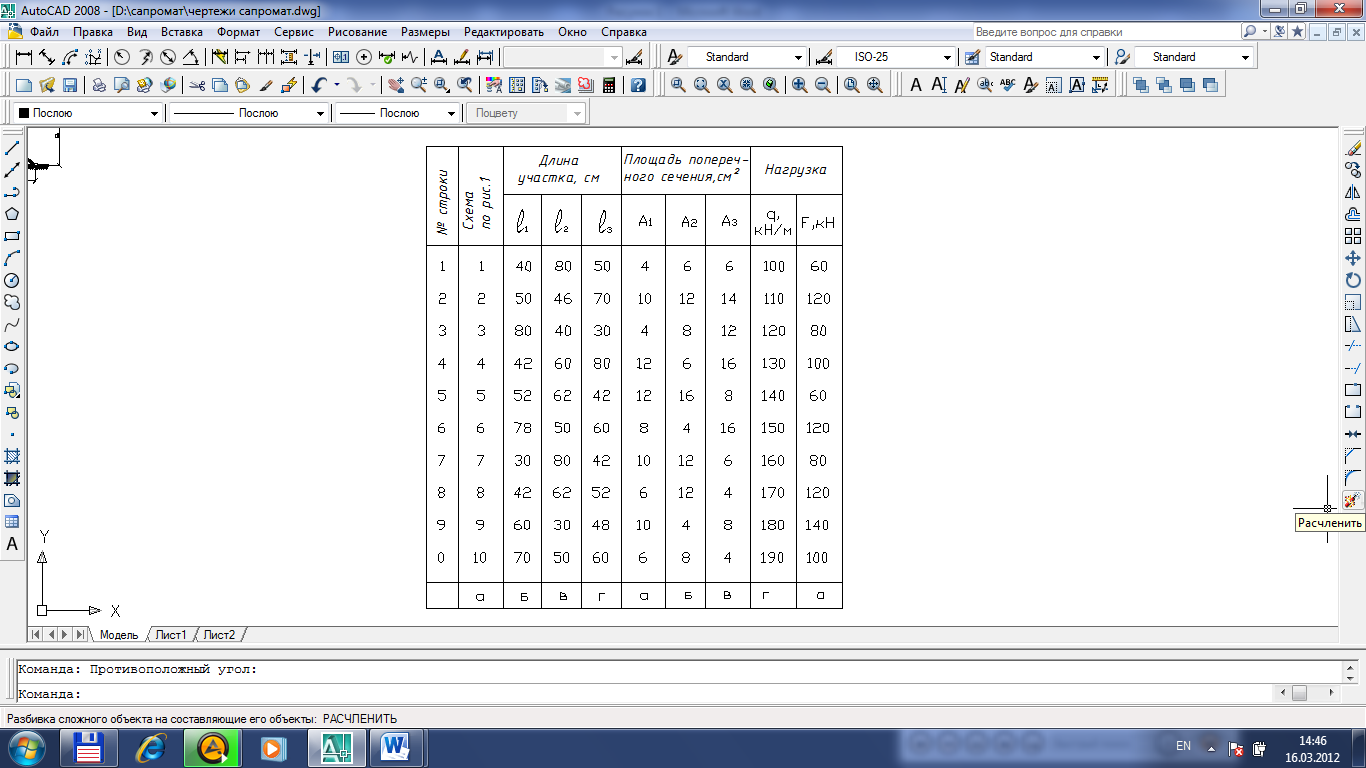
Материал бруса – сталь с расчетным сопротивлением МПа,

Е = 2 МПа.

Решение:

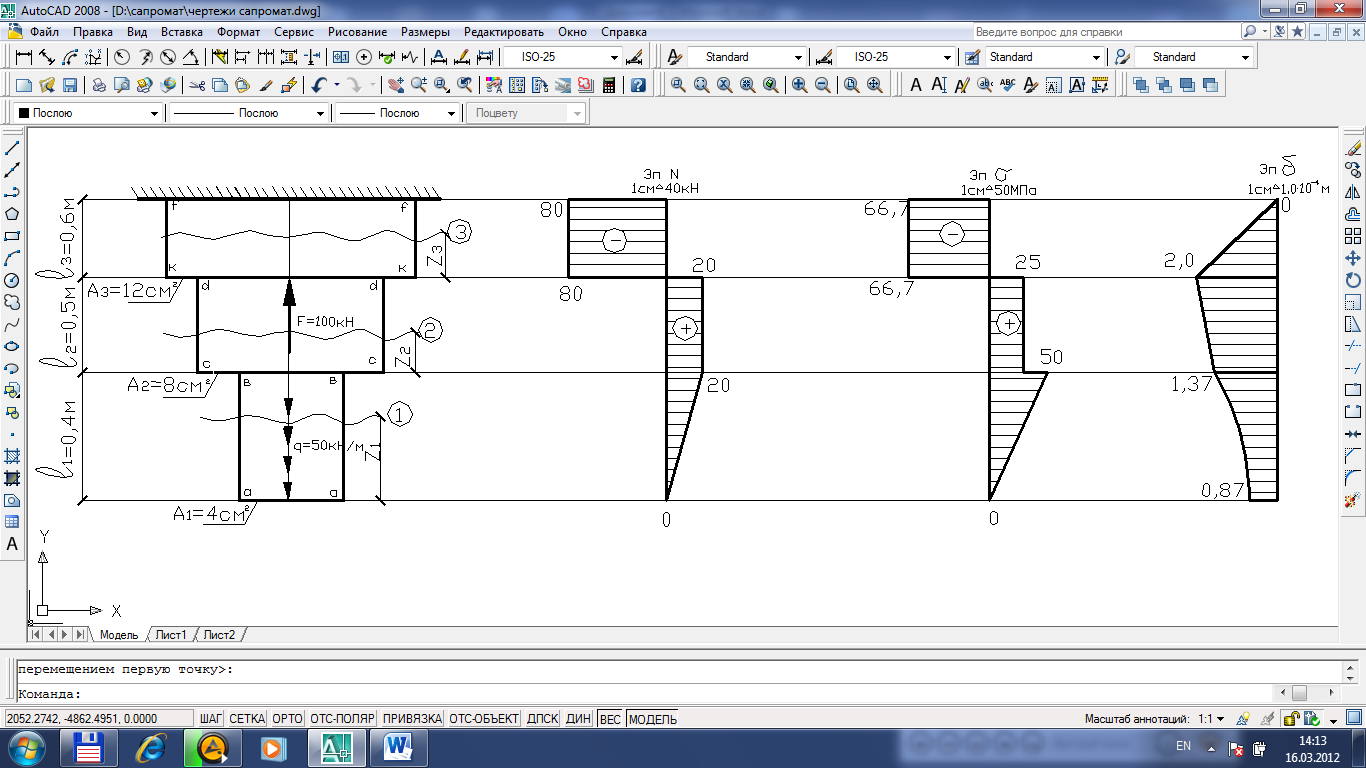
Рисунок 1.1- Схема бруса. Эпюры продольных сил, нормальных напряжений и перемещений поперечных сечений

1. Применив метод сечений (РОЗУ, т.е. мысленно рассекаем брус, отбрасываем его часть, заменяем влияние отброшенной части усилием N_i и уравновешиваем), записываем аналитическое выражение для продольной силы, после чего рассчитываем нормальное напряжение.

Примечание: Чтобы знак «+» соответствовал растяжению на участке, а знак «–» сжатию, нужно внутреннюю силу (N_i) прикладывать от сечения.

Участок 1

при Z₁= 0; N_а = 50·0=0; , где А₁ = 4 см²

при Z₁ = 0,4 м; N_b = 50·0,4=20 кН, МПа;.

Участок 2

при Z₂= 0; N_с = 50·0,4 = 20 кН; МПа;

при Z₂ = 0,5 м; N_d = 50·0,4=20 кН, МПа;.

Участок 3

при Z₃= 0; N_к = 50·0,4 – 100 = – 80 кН; МПа;

при Z₃ = 0,6 м; N_f = 50·0,4 – 100 = –80 кН, МПа;.

Строим эпюры N и по длине бруса.

2. Определяем перемещения сечений участков.

Так как брус жестко закреплен, то ;

а) определяем перемещение сечения относительно сечения f:

, где – абсолютная деформация участка 3.

Абсолютную деформацию участка можно определить по формуле:

или , тогда

м. (сжатие).

б) определяем абсолютную деформацию участка 2:

м. (растяжение).

Тогда перемещение сечения «С» относительно заделки составит:

м. (сжатие).

в) определяем абсолютную деформацию участка 1:

, где – площадь эпюры N₁ на первом участке.

м. (растяжение).

Тогда перемещение сечения «а» относительно заделки будет:

м.

3. Проверяем брус на прочность.

Анализируя эпюру напряжений, видим, что наиболее опасными являются сечения на третьем участке, где .

Условие прочности выполняется.

4. Проверяем брус на жесткость [ ]

м < [ ] м.

Условие жесткости выполняется.