
- •Введение
- •Определение производной. Дифференцируемость функции
- •Правила дифференцирования
- •Производная обратной функции
- •Производная сложной функции
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для самостоятельного решения
- •Рекомендуемая литература
- •Логарифмическое дифференцирование
- •Показательно-степенная функция.
- •Рекомендуемая литература
- •Повторное дифференцирование.
- •Решение.
- •Производная функции заданной параметрическими уравнениями.
- •Решение
- •Решение.
- •Задания для самостоятельной работы.
- •Рекомендуемая литература
- •Контрольная работа «Техника дифференцирования» Вариант №1 Вариант №2
- •Вариант №3 Вариант №4
- •Вариант №5 Вариант №6
- •Вариант №7 Вариант №8
- •Вариант №9 Вариант №10
- •Геометрический и физический смысл производной Геометрический смысл производной
- •Решение
- •Решение
- •Решение
- •Решение
- •Физический смысл производной
- •Решение
- •Решение
- •Задания для самостоятельной работы.
- •Рекомендуемая литература
- •Правило Лопиталя
- •Рекомендуемая литература
- •Исследование функций с помощью производных
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для самостоятельной работы
- •Рекомендуемая литература
- •Производная вектор – функции
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для самостоятельной работы
- •Рекомендуемая литература
- •Типовые задания Варианты примеров к типовому заданию.
- •Типовые задания Варианты примеров к типовому заданию.
- •4. Задачи на геометрический смысл производной.
- •5. Задачи на механический и физический смысл производной.
- •Найти наибольшее и наименьшее значения функции на отрезке.
- •7. Вычислить пределы функций с помощью правила Лопиталя.
- •8. Исследовать функцию и построить график.
- •Контрольная работа « Техника дифференцирования сложной функции»
Решение
Вычислим производную первого порядка


Теперь вычислим
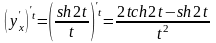
Подставим вычисления в формулу (1)

Ответ:

Пример
6.

Решение.


 ;
;
 - находится как производная частного
по переменной t:
- находится как производная частного
по переменной t:

 .
.
Ответ:

Задания для самостоятельной работы.
Вариант №1 Вариант №2
1. Найти производные третьего 1. Найти производные третьего
порядка
от функций: порядка от
функций:
а)
 а)
а)

б)
 б)
б)
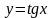
в)
 в)
в)
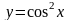
2.
Найти
 и
и
 :
2. Найти
и
:
:
2. Найти
и
:
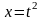 ,
,

 ,
,

3. Найти : 3. Найти :
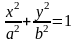

Вариант №3 Вариант №4
1. Найти производные третьего 1. Найти производные третьего
порядка
от функций: порядка от
функций:
а)
 а)
а)
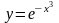
б)
 б)
б)

в)
 в)
в)

2. Найти и : 2. Найти и :
 ,
,
 ,
,

3. Найти : 3. Найти :


Вариант №5 Вариант №6
1. Найти производные третьего 1. Найти производные третьего
порядка
от функций: порядка от
функций:
а)
 а)
а)

б)
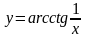 б)
б)

в)
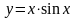 в)
в)

2. Найти и : 2. Найти и :
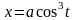 ,
,
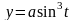
 ,
,

3. Найти : 3. Найти :

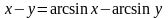
Вариант №7 Вариант №8
1. Найти производные третьего 1. Найти производные третьего
порядка
от функций: порядка от
функций:
а)
 а)
а)

б)
 б)
б)

в)
 в)
в)

2.
Найти
и
![]() :
2. Найти
и
:
:
2. Найти
и
:
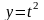 ,
,

 ,
,

3. Найти : 3. Найти :

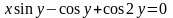
Вариант №9 Вариант №10
1. Найти производные третьего 1. Найти производные третьего
порядка
от функций: порядка от
функций:
а)
 а)
а)

б)
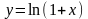 б)
б)
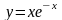
в)
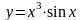 в)
в)

2. Найти и : 2. Найти и :
 ,
,

 ,
,

3. Найти : 3. Найти :

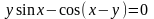
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Что называется производной высшего порядка?
Вычислите производную третьего порядка от функции
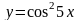 .
.Вычислите производную второго порядка от функции
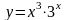 ,
используя формулу Лейбница.
,
используя формулу Лейбница.Преобразуйте формулу для вычисления производной второго порядка от функции, заданной параметрическими уравнениями
( для этого подставьте в числитель производную и используйте правило вычисления производной от частного).
Вычислите производную от функции

Найдите производную от функции, заданной неявно:
 .
.
