
- •Введение
- •Определение производной. Дифференцируемость функции
- •Правила дифференцирования
- •Производная обратной функции
- •Производная сложной функции
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для самостоятельного решения
- •Рекомендуемая литература
- •Логарифмическое дифференцирование
- •Показательно-степенная функция.
- •Рекомендуемая литература
- •Повторное дифференцирование.
- •Решение.
- •Производная функции заданной параметрическими уравнениями.
- •Решение
- •Решение.
- •Задания для самостоятельной работы.
- •Рекомендуемая литература
- •Контрольная работа «Техника дифференцирования» Вариант №1 Вариант №2
- •Вариант №3 Вариант №4
- •Вариант №5 Вариант №6
- •Вариант №7 Вариант №8
- •Вариант №9 Вариант №10
- •Геометрический и физический смысл производной Геометрический смысл производной
- •Решение
- •Решение
- •Решение
- •Решение
- •Физический смысл производной
- •Решение
- •Решение
- •Задания для самостоятельной работы.
- •Рекомендуемая литература
- •Правило Лопиталя
- •Рекомендуемая литература
- •Исследование функций с помощью производных
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для самостоятельной работы
- •Рекомендуемая литература
- •Производная вектор – функции
- •Решение
- •Решение
- •Решение
- •Решение
- •Задания для самостоятельной работы
- •Рекомендуемая литература
- •Типовые задания Варианты примеров к типовому заданию.
- •Типовые задания Варианты примеров к типовому заданию.
- •4. Задачи на геометрический смысл производной.
- •5. Задачи на механический и физический смысл производной.
- •Найти наибольшее и наименьшее значения функции на отрезке.
- •7. Вычислить пределы функций с помощью правила Лопиталя.
- •8. Исследовать функцию и построить график.
- •Контрольная работа « Техника дифференцирования сложной функции»
Рекомендуемая литература
1. Бугров, Я.С. Дифференциальное и интегральное исчисление. Учебник. В 2 т. Т. 1 / Я.С. Бугров, С.М. Никольский. - Ростов н/Д.: Феникс, 1997. - 512 с.
2. Кудрявцев, Л.Д. Краткий курс математического анализа / Л.Д. Кудрявцев. - М.: Наука, 1989. - 736 с.
Пискунов, Н.С. Дифференциальное и интегральное исчисление. В 2 кн. Кн. 1 / Н.С. Пискунов. - М.: Интеграл- Пресс, 2002. - 416 с.
Занятие 2
Логарифмическое дифференцирование
Иногда, для нахождения производной функцию сначала целесообразно прологарифмировать. Такую операцию называют логарифмическим дифференцированием. Логарифмическое дифференцирование применяют:
а) в случае, если - есть показательно-степенная функция;
б) в случае, если функция представлена в виде произведения степенных функций с различными показателями.
Показательно-степенная функция.
Функцию
вида
 ,
,
 ,
где и основание и показатель изменяются
вместе с независимой переменной, называют
показательно-степенной (или
степенно-показательной). Простейшим
примером такой функции является функция
,
где и основание и показатель изменяются
вместе с независимой переменной, называют
показательно-степенной (или
степенно-показательной). Простейшим
примером такой функции является функция
 ,
,
 .
Дифференцировать показательно-степенную
функцию можно следующим образом:
.
Дифференцировать показательно-степенную
функцию можно следующим образом:
1способ. Для нахождения производной этой функции можно использовать логарифмическое дифференцирование.
Для чего прологарифмируем данную функцию по основанию e:
![]() ,
и по свойству логарифма степени имеем:
,
и по свойству логарифма степени имеем:
 .
.
Продифференцируем
обе части этого равенства, с учетом
того, что y
– это функция, зависящая от x,
получим:
 .
.
Умножим обе части этого равенства на y, получим:
 .
.
Пример
1.
 .
.
Решение
Прологарифмируем
функцию y:
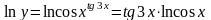 .
.
Найдем
производную:

Умножим
обе части на y:

2 способ. Производную от показательно-степенной функции можно находить как производную от показательной функции плюс производная от степенной функции (по формуле Г.Лейбница и И.Бернулли).

Пример
2.
 .
.
Решение

3
способ. Производную от показательно-степенной
функции можно найти, используя свойство
логарифма (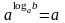 ).
).
Пример
3.
 .
.
Решение
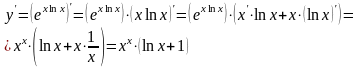
Произведение степенных функций с различными показателями
Логарифмическое дифференцирование может быть применено для отыскания производных не только функций показательно-степенного типа. Так, например, для отыскания производной от произведения функций с различными показателями удобно применять логарифмическое дифференцирование, что позволяет быстрее получить результат.
Пример
4.
 .
.
Решение
Прологарифмируем
функцию:
 ,
далее, используя свойства логарифмов,
запишем:
,
далее, используя свойства логарифмов,
запишем:
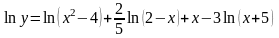 .
.
Найдем производные от обеих частей этого равенства, с учетом того, что - функция, зависящая от :
 .
.
Умножим обе части равенства на :

Задания для самостоятельной работы
Вариант №1 Вариант №2
Найти производные функций: Найти производные функций:
1.
 1.
1.

2.
 2.
2.

3.
 3.
3.
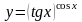
4.
 4.
4.
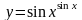
5.
 5.
5.

6.
 6.
6.

Вариант №3 Вариант №4
Найти производные функций: Найти производные функций:
1.
 1.
1.

2.
 2.
2.

3.
 3.
3.

4.
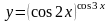 4.
4.
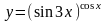
5.
 5.
5.
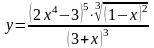
6.
 6.
6.

Вариант №5 Вариант №6
Найти производные функций: Найти производные функций:
1.
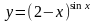 1.
1.
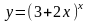
2.
 2.
2.

3.
 3.
3.

4.
 4.
4.

5.
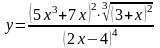 5.
5.

6.
 6.
6.

Вариант №7 Вариант №8
Найти производные функций: Найти производные функций:
1.
 1.
1.
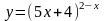
2.
 2.
2.

3.
 3.
3.

4.
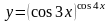 4.
4.

5.
 5.
5.

6.
 6.
6.
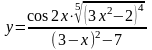
Вариант №9 Вариант №10
Найти производные функций: Найти производные функций:
1.
 1.
1.
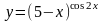
2.
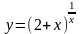 2.
2.
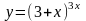
3.
 3.
3.

4.
 4.
4.

5.
 5.
5.

6.
 6.
6.
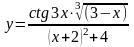
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Какую операцию называют логарифмическим дифференцированием?
2. Какая функция называется показательно- степенной?
3. Найдите производные от следующих функций:
а)

б)
в)

