Решение
Здесь выполняются следующие операции:
1)
возведение x в квадрат и сложение
результата с единицей:
;
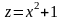2)
извлечение корня:
;
3)
взятие котангенса:
4)
возведение в куб:
;
5)
взятие показательной функции:
Итак:
;
;
;
;
.
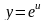Последняя операция - взятие показательной функции.
При дифференцировании сложной функции нужно выделить последнюю операцию в ее аналитическом выражении, и объект этой операции (т.е. величину, над которой операция производится) обозначить буквой, например, «u». Это «u» будет играть роль промежуточной переменной, Затем следует применить правило (2). Потом снова выделить последнюю операцию уже в промежуточной функции и опять применить формулу (2) и т.д.
Пример 5. Найти производную функции .
Решение
Как отмечено в примере 1, здесь последняя операция - возведение в куб:
По формуле 1) из (3)
,
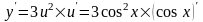а по формуле 5) из (1)
,
так
что
.
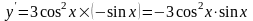Пример
6. Найти производную функции
.
Решение
Здесь последняя операция - извлечение корня (см. пример 2). Ее объект (подкоренное выражение) обозначим u, так что:
,
где
.
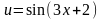По формуле 1) из (3)
.
В выражении для u последняя операция - взятие синуса (см. пример 2). Ее объект обозначим v:
По формуле 4) из (3)
Наконец, 
.
Итак,
Пример 7. Найти производную функции .
Решение
Как показано в примере 3, здесь последняя операция - возведение в степень с показателем . Основание степени обозначим u:
,
где
.
По формуле 1) из (3):
;
В выражении для u (см. пример 3) последняя операция - взятие логарифма. Ее объект обозначим v:
,
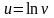где
По формуле 3) из (3):
;
В выражении для v последняя операция - взятие косинуса. Ее объект обозначим w:
.
По формуле 5) из (3)
.
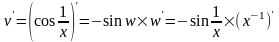Производная w = x -1 находится по формуле 1) из (1):
;
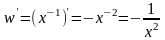Таким образом, окончательный результат:
.
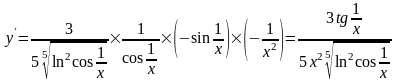После некоторой тренировки запись можно вести так:
.
Пример
8. Найти производную функции
.
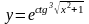Решение
Здесь последняя операция - взятие показательной функции (см. пример 4) Ее объект (показатель) обозначим u, так что:
,
где
.
По формуле 2) из (3)
.
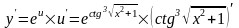В выражении для u последняя операция - возведение в куб. Основание степени обозначим v:
,
.
По формуле 1) из (3):
.
В
выражении для
последняя операция - взятие котангенса:
,
;
По формуле 7) из (3)
.
В
выражении для
последняя операция - извлечение корня.
, ;
По формуле 1) из (3):
.
Наконец, производная может быть взята по таблице (1) с учетом правила дифференцирования суммы:
.
Итак,
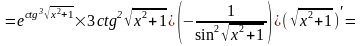
. (4)
После некоторой тренировки результаты промежуточных операций (промежуточные переменные) можно обозначать буквами лишь мысленно, а запись вести в виде (4).
Пример
9. Найти производную функции
.
Решение
Здесь выполняются следующие операции: 1) возведение в 5-ю степень; 2) взятие косинуса; 3) взятие логарифма; 4) возведение в квадрат. Последняя операция - возведение в квадрат. Дифференцируем эту операцию.
.
В скобках последняя операция - логарифм. Дифференцируем эту операцию.
.
Теперь в скобках последняя операция - косинус.
Ее производная
.
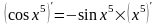Наконец, 
.
Итак,
.
Пример
10. Найти производную функции
.