5. Задачи на механический и физический смысл производной.

1. Точка движется прямолинейно по закону Найти скорость и ускорение движения через 1с. после начала движения.

2. Закон прямолинейного движения точки выражается формулой . Найти скорость и ускорение в момент времени

3. Точка движется по оси абсцисс по закону . В какой момент времени точка остановится?

4. Тело массой 5кг движется прямолинейно по закону Найти кинетическую энергию тела 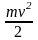через две секунды после начала движения.

5. Вращающееся колесо задерживается тормозом. Угол , на который колесо поворачивается в течение 1с, определяется равенством Найти угловую скорость и угловое ускорение через 2с после включения тормоза.

6. Тело движется по закону :

а) показать, что его ускорение численно равно пройденному пути;

б) найти путь и ускорение через 1 с, если .

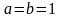7. Закон прямолинейного движения выражается формулой 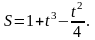Найти скорость и ускорение в момент времени c.

8. Скорость прямолинейного движения тела пропорциональна квадратному корню из пройденного пути S (как, например, при свободном падении тела). Доказать, что тело движется под действием постоянной силы. Найти ускорение, если коэффициент пропорциональности равен 2.

9. Тело движется по прямой ОХ по закону 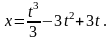Определить скорость и ускорение движения в момент времени c.

10. Колебательное движение материальной точки совершается по закону определить скорость и ускорение движения в точке x=0.

11. Тело движется по прямой ОХ по закону В какие моменты времени тело меняет направление движения?

12. Колесо вращается так, что угол поворота пропорционален кубу времени. Первые два оборота сделаны колесом за 4 с. Найти угловую скорость через:

а) 16 с после начала движения;

б) 8 с после начала движения.

13. Точка движется прямолинейно так, что 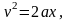где v – скорость, x – пройденный путь, a – постоянная. Определить ускорение движения при x=8.

14. Зависимость между количеством x вещества, полученного в некоторой химической реакции, и времени t выражается формулой Определить скорость реакции в момент, когда t=2 c.

15. Закон прямолинейного движения точки выражается формулой Найти скорость и ускорение движения в момент времени t=3.

16. Тело массой 10 кг движется прямолинейно по закону Найти кинетическую энергию тела через 1 с после начала движения.

17. Вращающееся колесо задерживается тормозом. Угол , на который колесо поворачивается, определяется равенством Определить, в какой момент времени колесо останавливается.

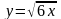18. Точка движется по параболе так, что абсцисса возрастает со скоростью 10 м/с. какова скорость изменения ординаты этой точки в момент, когда: а) х=6; б) х=24?

19. Сторона квадрата увеличивается со скоростью 5 см/с. С какой скоростью изменяется площадь квадрата, когда сторона достигает 15 см?

20. Колебательное движение точки совершается по закону Определить скорость и ускорение движения в точке х=0, если 0<t< .

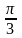21. Зависимость между количеством х вещества, полученного в некоторой химической реакции, и времени t выражается уравнением Определить скорость в момент времени t=1 c и k=-1.

22. Вращающееся колесо задерживается тормозом. Угол , на который колесо поворачивается, определяется равенством 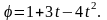Определить, в какой момент времени колесо останавливается.

23. Точка движется прямолинейно по закону Чему равны скорость и ускорение в момент времени: а) t=2; б)t=1/2?

24. Количество электричества, протекающее через проводник, начиная с момента времени t=0, задается формулой В какие моменты времени сила тока в проводнике равна: а) 0; б) 15?

25. Угол , на который поворачивается колесо через t c, равен 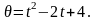Через сколько времени угловая скорость будет равна: а)0; б) 2?

26. Радиус шара равномерно возрастает со скоростью 5 м/с. С какой скоростью растут площадь поверхности шара и его объем в момент, когда его радиус становится равным: а) 50 см; б) 500 см?

27. Концы отрезка АВ, длина которого равна 5 м, скользят по осям координат в первой четверти. Скорость перемещения конца А равна 2 см/с. Какова скорость перемещения верхнего конца В в тот момент, когда конец А находится от начала координат на расстоянии см.

28. Тело массой 6 г движется прямолинейно по закону , (S – в см, t – в с). Требуется вычислить кинетическую энергию через 1 с после начала движения.

29. Зависимость пути от времени при прямолинейном движении точки выражается формулой 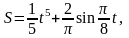(S – в м, t – в с). Определить скорость движения в конце второй секунды.

30. Тело движется по закону

а) определить скорость и ускорение;

б) в какие моменты времени тело меняет направление движения?