Решение

1. Найдем критические точки функции, лежащие внутри отрезка. Для этого воспользуемся необходимым условием экстремума.

2. Вычислим значения функции на концах отрезка и в критической точке:

.

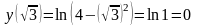3. Среди вычисленных значений выберем наименьшее и наибольшее:

.

Ответ: .

Кривая называется выпуклой на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая называется вогнутой на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале.

Промежутки выпуклости и вогнутости кривой определяются по знаку производной второго порядка.

Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба.

Необходимое условие точки перегиба. Если в точке перегиба функции существует производная второго порядка, то она равна нулю, то есть .

Точки, для которых выполняется необходимое условие перегиба, называются точками, подозрительными на перегиб.

Достаточное условие точки перегиба. Если для точки выполняется необходимое условие перегиба, и при переходе через эту точку производная второго порядка меняет знак (не важно с какого на какой), то точка является точкой перегиба кривой .

Таким образом, с помощью производной второго порядка определяются промежутки выпуклости и вогнутости и точки перегиба. Делается это следующим образом.

1. Находятся точки, подозрительные на перегиб, используя необходимое условие перегиба. Для этого вычисляется производная второго порядка и приравнивается к нулю.

2. Область определения функции разбивается точкой, подозрительной на перегиб, на промежутки и определяется знак производной второго порядка в каждом промежутке. По знаку производной определяются промежутки выпуклости и вогнутости, а по достаточному условию перегиба – точки перегиба.

Пример 3. Определить промежутки выпуклости и вогнутости и найти точки перегиба графика функции .

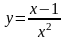Решение

Область определения функции: .

1. Найдем точки, подозрительные на перегиб, используя необходимое условие перегиба. Для этого вычислим производную второго порядка и приравняем ее к нулю.

- точка, подозрительная на перегиб.

2. Разобьем область определения функции точкой, подозрительной на перегиб, на промежутки и определим знак производной второго порядка в каждом промежутке.

3. Результаты занесем в таблицу:

		0		3
	_	не сущ.	_	0	+
	выпуклая	не сущ.	выпуклая	точка перегиба	вогнутая

Ответ: точка - точка перегиба,

на промежутках и кривая выпуклая,

на промежутке кривая вогнутая.

Исследуем функцию .

1. Область определения функции D(x).

2. Область значений функции Е(у).

3. Четность, нечетность функции.

Если функция четная, то ее график симметричен относительно оси ОУ.

Если функция нечетная, то ее график симметричен относительно начала координат. Таким образом, в случае четной (или нечетной функций), их можно исследовать на положительной половине числовой прямой, а результаты исследований продлить на отрицательную полуось.

4.Периодичность функции.

Периодическими являются тригонометрические функции. Их можно исследовать на одном промежутке периода, а результаты исследований продлить на всю числовую прямую.

5.Точки пересечения графика с осями координат.

Этот пункт выполняется для точности построения графика.

Точку пересечения с осью ОУ найдем, решив уравнение .

Точку пересечения с осью ОХ найдем, решив уравнение .

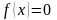6.Асимптоты графика функции.

Прямая называется асимптотой кривой, если расстояние от переменной точки М кривой до этой прямой при удалении точки М в бесконечность стремится к нулю.

Отличают асимптоты вертикальные, горизонтальные и наклонные:

а) если для функции выполнено хотя бы одно из условий:

, или , или ,

то прямая называется вертикальной асимптотой функции ;

в) если существует конечный предел , то прямая называется горизонтальной асимптотой;

с) прямая называется наклонной асимптотой, если существуют конечные пределы:

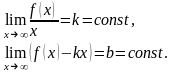
Замечание: при наклонная асимптота становится горизонтальной.

7. Промежутки монотонности и точки экстремума.

Промежутки монотонности и точки экстремума найдем с помощью производной первого порядка.

8. Промежутки выпуклости, вогнутости и точки перегиба.

Промежутки выпуклости, вогнутости и точки перегиба найдем с помощью производной второго порядка.

9. График функции.

График функции строим следующим образом:

а) строим асимптоты;

б) отмечаем точки пересечения графика с осями координат, точки экстремума и точки перегиба;

в) соединяем полученные точки в соответствии с промежутками монотонности, промежутками выпуклости, вогнутости и асимптотами.

Пример 4. Исследовать функцию и построить ее график.