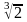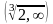Рекомендуемая литература

1. Бугров, Я.С. Дифференциальное и интегральное исчисление. Учебник. В 2 т. Т. 1 / Я.С. Бугров, С.М. Никольский. - Ростов н/Д.: Феникс, 1997. - 512 с.

2. Кудрявцев, Л.Д. Краткий курс математического анализа / Л.Д. Кудрявцев. - М.: Наука, 1989. - 736 с.

3. Пискунов, Н.С. Дифференциальное и интегральное исчисление. В 2 кн. Кн. 1 / Н.С. Пискунов. - М.: Интеграл- Пресс, 2002. - 416 с.

Занятие 7

Исследование функций с помощью производных

Промежутки возрастания и убывания функции называются промежутками монотонности.

Промежутки монотонности определяются по знаку производной первого порядка..

Точка называется точкой минимума функции , если существует такая окрестность этой точки, для всех точек которой выполняется условие .

Точка называется точкой максимума функции , если существует такая окрестность этой точки, для всех точек которой выполняется условие .

Точки минимума и максимума называются точками экстремума.

Необходимое условие экстремума. Если точка является точкой экстремума функции , то производная от функции в этой точке либо равна нулю, либо не существует.

Точки, для которых выполняется необходимое условие экстремума, называются критическими или подозрительными на экстремум.

Достаточное условие экстремума. Пусть функция непрерывна в некотором интервале, содержащем критическую точку , и дифференцируема во всех точках интервала (кроме, может быть, самой точки ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при функция имеет максимум, а если с минуса на плюс, то функция в этой точке имеет минимум.

Таким образом, с помощью производной первого порядка для функции можно найти промежутки монотонности и точки экстремума. Делается это следующим образом.

1. Находятся критические точки, используя необходимое условие экстремума. Для этого вычисляется производная и приравнивается к нулю.

2. Область определения функции разбивается критическими точками на промежутки и определяется знак производной в каждом промежутке. По знаку производной определяются промежутки монотонности, а с использованием достаточного условия экстремума – точки экстремума.

Пример 1. Определить промежутки монотонности и точки экстремума функции .

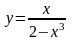Решение

Область определения функции: .

1. Найдем критические точки, используя необходимое условие экстремума.

Для этого вычислим производную и приравняем ее к нулю:

- критические точки.

2. Разобьем область определения функции критическими точками на промежутки и определим знак производной в каждом промежутке. Результаты занесем в таблицу:

		-1
	_	0	+	не сущ.	+
	убывает	точка минимума	возрастает	не сущ.	возрастает

Ответ: - точка минимума, - промежуток убывания, - промежутки убывания.

С помощью производной первого порядка можно определить также наименьшее и наибольшее значения функции на отрезке. Эти значения находятся среди точек экстремума внутри отрезка и значений функции на концах отрезка.

Пример 2. Найти наименьшее и наибольшее значения функции на отрезке .