Г.А. ЛЕСКОВА

М.Г. МИНАЕВА

ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Учебное пособие

Чита 2008

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«ЧИТИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ЧитГУ)

Г.А. Лескова

М.Г. Минаева

ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Учебное пособие

для студентов технических специальностей

Чита 2008

ПРЕДИСЛОВИЕ

Настоящее учебное пособие рекомендовано для студентов технических специальностей, изучающих раздел математики «Дифференцирование функции одной переменной».

Пособие включает в себя 8 практических занятий по приобретению навыков вычисления производной. Разделения на занятия условные. В каждом занятии рассмотрены основные теоретические вопросы раздела, даны задания для самостоятельной работы и контрольная работа. Перед выполнением самостоятельных заданий рекомендуется изучить соответствующий теме занятия теоретический материал. После каждого занятия представлены контрольные вопросы.

В качестве промежуточного контроля в семестре даны типовые задания. В приложении подробно рассмотрены варианты выполнения контрольной работы.

При написании учебного пособия преподавателями был использован многолетний опыт лекционной и практической работы со студентами.

Пособие будет полезно и студентам заочной формы обучения, а также ассистентам кафедры математики.

Авторы будут признательны за отзывы, пожелания и замечания.

Введение

Дифференциальное исчисление является одним из основополагающих разделов математики.

Овладение техникой дифференцирования является необходимым условием успешного изучения дальнейших разделов математического анализа. Знакомство с производными сейчас начинается в средней школе. С учетом этого современная программа ВТУЗа отводит технике дифференцирования очень мало практических занятий. Между тем, большинство выпускников средней школы навыка дифференцирования не имеют. Время, необходимое для выработки данного навыка, у разных студентов оказывается весьма различным в зависимости от уровня их школьной подготовки и разрыв этот настолько велик, что практически невозможно спланировать аудиторные занятия по технике дифференцирования так, чтобы их было достаточно для выработки навыка у слабых студентов и в то же время эти занятия не были бы потеряны для более сильных. Поэтому самостоятельная работа при овладении техникой дифференцирования для части студентов неизбежна.

Настоящее учебное пособие призвано служить руководством в самостоятельной работе студентов по выработке навыка дифференцирования сложных функций и предназначено для студентов всех специальностей технического ВУЗа.

Изложение материала базируется на классических концепциях математики.

Занятие 1

Определение производной. Дифференцируемость функции

Пусть функция определена в некоторой области D. Зафиксируем аргумент и зададим ему приращение . Получим аргумент , которому соответствует значение функции . Разность

называется приращением функции в точке , соответствующим приращению аргумента .

Составим отношение приращения функции к приращению аргумента:

.

Если существует предел данного отношения при , то он называется производной от функции в точке , т.е. производной от функции в точке называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.

Производную принято обозначать так:

(1)

Для существования производной в точке необходимо, чтобы функция была определена в некоторой окрестности этой точки, в том числе и в самой точке.

Процесс нахождения производной называется дифференцированием.

Раздел математического анализа, занимающийся вопросами, связанными с производной, называется дифференциальным исчислением.

Если функция имеет производную в точке , то она называется дифференцируемой в этой точке.

Замечание: если говорят, что функция имеет производную в точке, то подразумевают, что этот предел (1) конечен. Но может случиться, что существует бесконечный предел (1), равный или . В этих случаях говорят, что функция имеет в точке бесконечную производную (равную 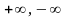, или ).

Если функция дифференцируема в точке (т.е. имеет конечную производную), то она непрерывна в этой точке.

Обратное утверждение неверно. Существуют функции, всюду непрерывные, но при некоторых значениях аргумента не имеющие производной.

Правила дифференцирования

Основные правила дифференцирования связаны с вычислением производных от арифметических действий.

Правило 1. Производная от суммы (или разности) двух дифференцируемых функций равна сумме (или разности) производных этих функций, т.е.

Правило 2. Производная произведения двух дифференцируемых функций равна произведению производной первой функции на неизменную вторую функцию плюс произведение первой функции на производную второй, т.е.

Правило 3. Производная дроби равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, т.е.

Правило 4. Производная постоянной величины равна нулю, т.е.

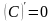, где С = соnst

Правило 5. Постоянный множитель можно выносить за знак производной, т.е. , где С = сonst