Лекция № 3. Тема 3 : Матрицы

3.1. Основные виды матриц

Определение 1. Матрицей называется совокупность чисел, располо-женных в т строках и п столбцах и обозначается

Число, стоящее на пересечении -ой строки и -го столбца, обозначается и называется элементом матрицы; размерность матрицы, что иногда обозначается

Существуют следующие виды матриц:

1. Матрица – строка

2. Матрица – столбец

3. Нулевая матрица  все ее элементы нули.

4. Единичная матрица

5. Диагональная матрица .

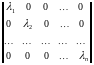6. Симметрическая матрица – для ее элементов выполняется равенство для всех

Важной характеристикой квадратной матрицы А является её опреде-литель, который обозначается Если 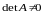, то матрица А назы-вается невырожденной. В противном случае – вырожденной.

_{Определение 2.} Две матрицы и одинаковой раз-мерности называются равными, если равны все их соответствующие эле-менты для всех

3.2. Действия над матрицами

1. Транспонирование матриц.

Определение 3. Транспонированием матрицы называется замена её строк столбцами с сохранением их номеров.

Транспонированная матрица обозначается А ^Т.

Пример 1. Найти А ^Т, если матрица

Тогда

2. Сложение матриц.

Определение 4. Суммой двух матриц и одинаковой размерности называется матрица С той же размерности, элементы которой определяются равенствами и обозначается .

3. Умножение матрицы на число.

Определение 5. Произведением матрицы на некоторое число называется матрица , элементы которой равны элементам матрицы А, умноженным на это число , т.е. и обозначается .

Пример 2. Найти матрицу , если

4. Умножение матриц.

Определение 6. Произведением матрицы размерности и матрицы размерности , называется матрица , размерности , элементы которой удовлетворяют равенству

и обозначается .

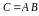Замечание 1. Как видно из определения, произведение двух матриц будет определено, если число столбцов первой матрицы равно числу строк второй.

Пример 3. Найти произведение матриц

Тогда

Замечание 2. Легко убедиться в том, что в общем случае произведение матриц не обладает коммутативным свойством, т.е. что видно из следующего примера.

Пример 4. Найти произведение матриц

Тогда имеем

3.3. Обратная матрица

Определение 7. Обратной матрицей матрицы А называется матрица , для которой выполняется равенство

Из этого определения следует, что понятие обратной матрицы является взаимообратным и определено только для квадратных матриц. При этом для существования обратной матрицы необходимо, чтобы матрица А была невырожденной, т.е. .

Покажем, что обратной матрицей для случая матрицы А размер-ности будет матрица

где  алгебраические дополнения элемента .

Тогда

Например,

и т.д.

Так же можно проверить и равенство

Замечание 4. Аналогично для матрицы А размерности обратная матрица имеет вид