1. Стационарное поведение.

Пусть имеется термопара, состоящая из двух проводов A и B, которые соединены друг с другом (рис. 1.6).

Места соединения A-B и B-A имеют различные температуры T_M (точка измерения) и T_E (холодный спай термопары). На основе эффекта Зеебека возникают напряжения U_M и U_E, которые являются пропорциональными соответствующей температуре. Из-за встречно-последовательной коммутации мест соединения возникает температурное напряжение U_T, которое пропорционально разнице температур T_M – T_E. Коэффициент пропорциональности K_AB − это термочувствительность, которая указывается в мВ на 100 градусов изменения температуры.

U_M = K_AB ^. T_M (1.4)

U_E = K_AB ^. T_E (1.5)

U_T = U_M – U_E = K_AB (T_M – T_E) (1.6)

Рис.1.6. Термопара сочетания металлов A-B без (a) и с подключением к медным проводам вывода, (b) и (c).

На практике металлы A и B постоянно соединены при помощи медных проводов с другим измерительным проводом, который каждый раз представляет термоэлектрическое действенное место соединения (A-Cu и B-Cu), температура которого T_E в большинстве случаев является температурой окружающей среды [см. рис. 1.6 (b)].

Тогда суммарное напряжение составит:

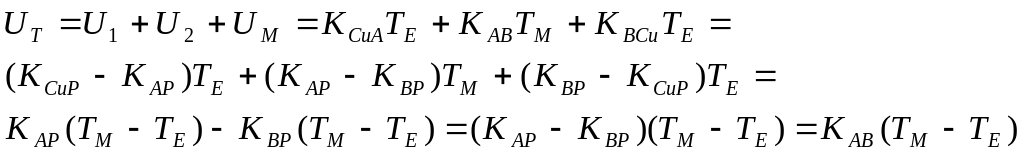(1.7)

где :К_АР, К_ВР – термочувствительности термопар А-Pt и В-Pt соответственно (Pt – платина берется в качестве эталонного металла).

Результат показывает, что третий металл, здесь медь, не имеет влияния на измеренное напряжение U_T, если оба места соединения Cu-A и B-Cu находятся при одной и той же температуре T_E.

Если желательно провести абсолютное измерение температуры T_M, то необходимо установить T_E в качестве эталонной температуры, например, T_E = 0 °C, что в лаборатории может происходить с использованием воды со льдом. Техническая схема на рис. 1.6 (c) по действию похожа на (b). Если между термопарой и измерительным прибором дополнительно используют компенсационный провод (AGL), то холодный спай термопары может находиться в месте, наиболее удаленном от точки измерения (например, в контрольно-измерительном пункте), где температура T_E относительно постоянна. Проводник компенсационного провода (AGL) имеет те же термоэлектрические характеристики, что и металлы термопары, с которыми температурное напряжение не создается. Нельзя присоединять компенсационный провод (AGL) с перепутанной полярностью. Вышеупомянутые линейные уравнения касаются только приближенно маленького диапазона температур. Для больших диапазонов температуры в точке измерения T_M должны проводиться коррекции для ее точного определения. В современных измерительных приборах это происходит благодаря электронной памяти табличного типа, в которых записаны соответствующие норме два взаимозависящих значения [ROM (ПЗУ)]. Исходя из этого, благодаря программе интерполяции микропроцессор вычисляет любой произвольный промежуточный результат.

2. Динамическое поведение.

Термопара состоит из тонких проводов, которые размещены в большинстве случаев в маленьком корпусе.

Рис. 1.7. Изменяющееся во времени напряжение U₀(t) термопары для скачка температуры ΔT = U_T/K_AB.

Исходя из этого исполнения, следствием является характер замедления первого порядка, узнаваемый при скачке температуры ΔT, как экспоненциальное переменное выходное напряжение U₀(t). U₀(t) стремится к стационарному значению U_T. Это поведение описывается дифференциальным уравнением, результат которого для ΔT отображен на рис. 1.7.

(1.8)

Дифференциальное уравнение показывает, что к любому произвольному моменту времени t (уже непосредственно в начале измерения в момент t = 0) может быть указано стационарное конечное значение U_T напряжения U₀ (t  ∞), в то время как к измеряемой величине U₀(t) прибавляется умноженное на постоянную времени τ дифференциальное отношение dU₀(t)/dt. При помощи собираемой аналоговой счетной схемы, которая решает эту задачу, легко достигается 10-кратная скорость реакции по сравнению с бескорпусной термопарой.