Постановка задачи
Для перевозки изделий, состоящих из двух контейнеров А и В, у компании «Транзит» имеются три транспортных средства разных типов, возможности которых приведены в таблице № 1. Перевозка двух различных контейнеров на одном транспортном средстве техническими условиями не допускается.
Необходимо разработать план перевозок, обеспечивающий доставку максимального числа изделий в комплекте за 24 часа, при условии что:
- простои и обратные перевозки не допускаются;
- перевозка двух различных контейнеров на одном транспортном средстве не допускается техническими условиями.
Таблица № 1 – Исходные данные задачи
Тип транспортных средств |
Производительность (ед./ч) |
|
Контейнер А |
Контейнер В |
|
Т1 |
5 |
5 |
Т2 |
6 |
2 |
Т3 |
5 |
3 |
1. Уяснение экономико-математической постановки задачи
Цель действий: Максимальная перевозка числа изделий в комплекте за сутки.
Цель математического моделирования: Определение эффективного плана перевозок.
Показатель эффективности определим из цели действия – ежедневное число перевезенных изделий в комплекте.
2. Разработка математической модели
По условию задачи нам неизвестно время перевозки транспортными средствами соответствующего типа контейнеров А и В. Обозначим это время как неизвестные переменные модели:
х1 – перевозка контейнера А транспортным средством первого типа;
х2 - перевозка контейнера А транспортным средством второго типа;
х3 - перевозка контейнера А транспортным средством третьего типа;
х4 – перевозка контейнера В транспортным средством первого типа;
х5 - перевозка контейнера В транспортным средством второго типа;
х6 - перевозка контейнера В транспортным средством третьего типа.
Доход, получаемый от перевозки изделий, является условной стоимостью. Обозначим его как сj. По условию задачи с1 = 5, с2 = 6, с3 = 5, с4 = 5, с5 = 2, с6 = 3. Тогда общий доход, получаемый от ежедневного числа перевезенных изделий можно представить в виде целевой функции:
Условие комплектности изделий является ограничивающим фактором на их перевозку и предполагает, что за 24 часа транспортные средства перевезут равное число контейнеров А и В. Это условие можно записать следующим образом:
Еще одним ограничивающим фактором являются требования отсутствия простоев и обратных перевозок. Требование отсутствия простоев, т.е. непрерывного использования всех транспортных средств в течение суток, можно записать следующим образом:
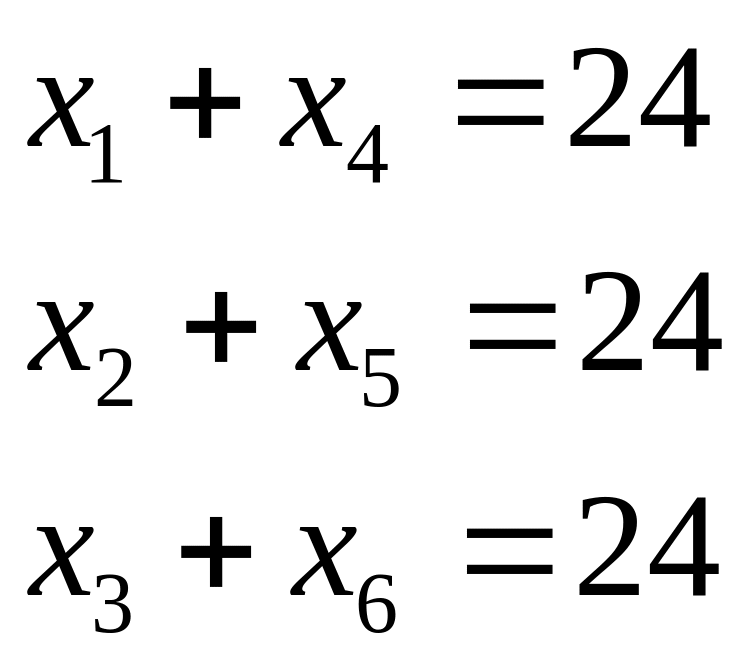
Требование отсутствия обратных перевозок можно записать в виде:
где 
Так как ПЭ и ограничения линейны, то данную задачу можно решить методом линейного программирования.
Таким образом, задача нахождения эффективного плана перевозок, обеспечивающего максимум перевозимых изделий в комплекте может быть сформулирована следующим образом:
Найти неотрицательные значения неизвестных переменных х1, х2 , х3, х4 , х5, х6 обращающих ЦФ в максимум:
,
при
удовлетворяющих системе линейных ограничений:
уравнений, задающих условия решения задачи
и ограничений на переменные
где
Данная постановка задачи имеет множество решений т.к. m = 4 < 6 = n.