- •Допустимі питомі навантаження в шарнірі ланцюга
- •Ланцюг втулково-роликовий однорядний Місце маркування
- •Перелік використаних джерел
- •До розрахунку передач
- •Вибір матеріалу, термообробки і твердості
- •Коефіцієнт ширини вінця відносно діаметра колеса ψbd
- •Нормальні лінійні розміри, мм
- •Основні параметри редукторів
- •Модуль m і коефіцієнт діаметра черв’яка q
- •Значення динамічного коефіцієнта тертя для різних матеріалів
- •До розрахунку пасових передач
- •До розрахунку ланцюгових передач
- •Приводні, роликові, втулкові ланцюги по дсту гост 13568:2006 (исо 3912-77), idt
- •До розрахунку підшипників ковзання
- •Допустимі режими роботи підшипникових матеріалів
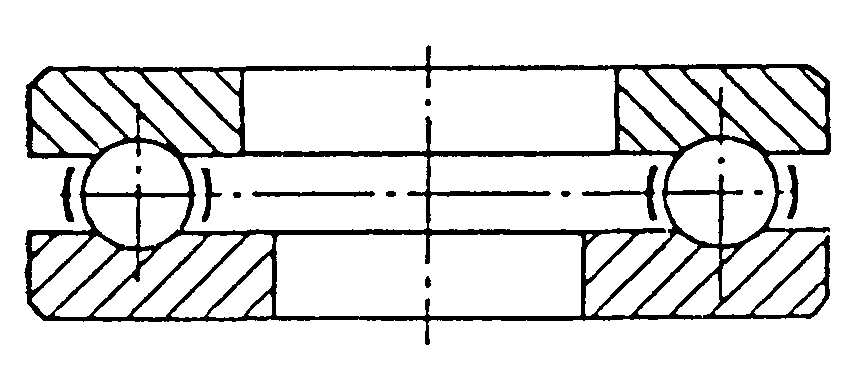
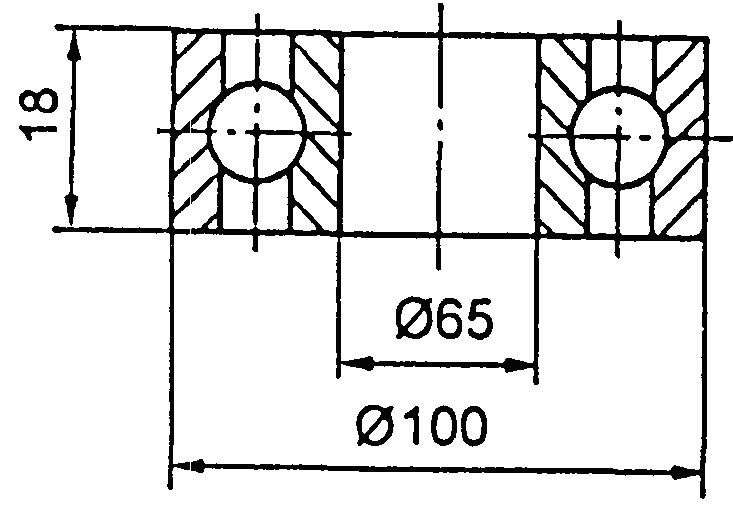
- •Кулькові підшипники однорядні (дсту гост 8338:2008)
- •Р оликові підшипники радіальні з короткими циліндричними роликами (гост 8328 - 75)
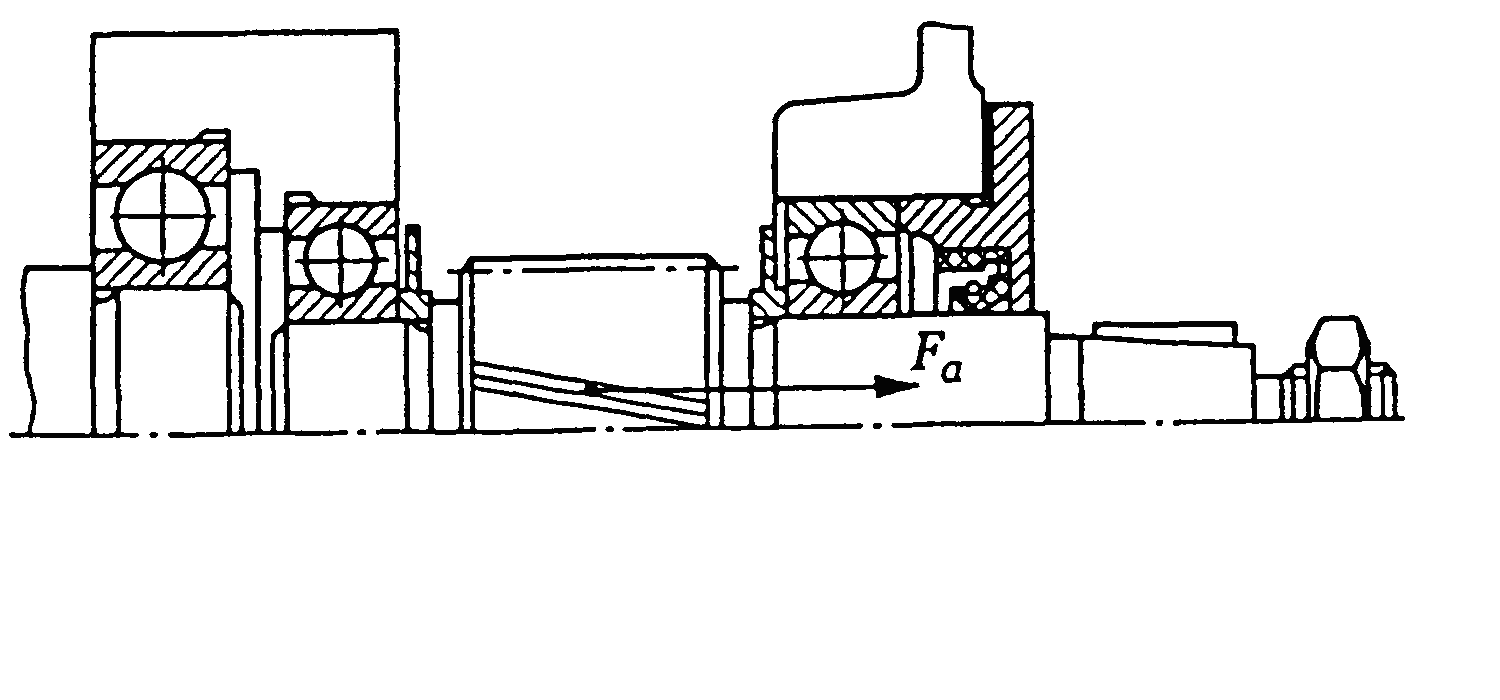
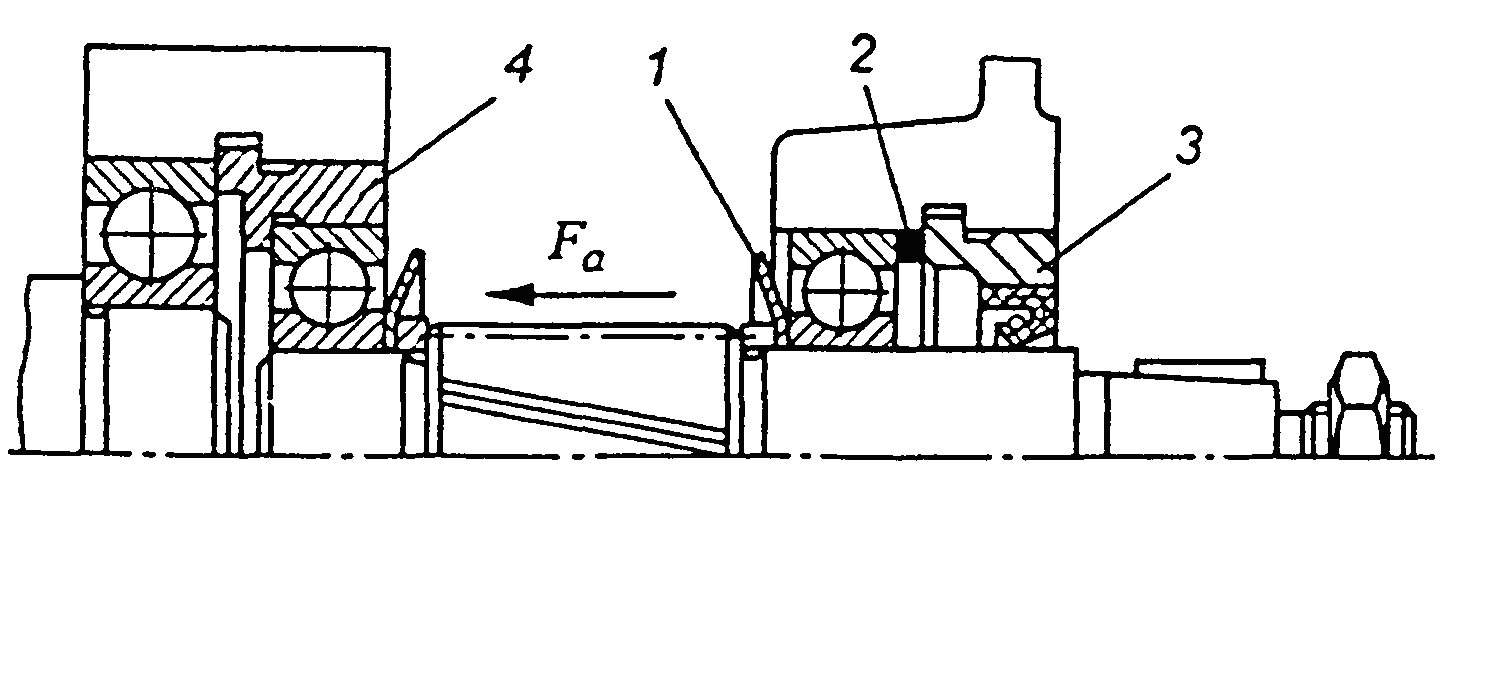
- •Кулькові підшипники радіально-упорні однорядні (гост 831-75)
- •Роликові конічні однорядні підшипники
- •Значення коефіцієнтів довговічності а1 при різній імовірності безвідмовної роботи
- •Рекомендовані значення коефіцієнта а23
- •Значення X, y, e для радіальних і радіально-упорних кулькових підшипників
- •Значення X, y, e для радіальних і радіально-упорних кулькових підшипників
- •Значення коефіцієнта k, який враховує умови експлуатації привода
- •До розрахунку різьбових з’єднань
- •До розрахунку шпонкових і шліцевих з’єднань
- •З’єднання шліцьові евольвентні (гост 6033-80)
- •До розрахунку заклепкових з’єднань
- •Види заклепкових з’єднань
- •До розрахунку зварних з’єднань
- •Приклади змістовних модулів
- •76000, М. Івано-Франківськ, вул. С. Бандери, 1
Міністерство освіти і науки України
Івано-Франківський національний технічний
університет нафти і газу
О.І. Вольченко, В.С. Ловейкін, Д.Ю. Журавльов, В.Я. Малик
КУРС ЛЕКЦІЙ З ДЕТАЛЕЙ МАШИН
ТА ТЕСТОВІ ЗАВДАННЯ
Навчальний посібник
Івано-Франківськ
2010
УДК 621.81 (075)
ББК 344.44
С31
Рекомендовано вченою радою університету
(протокол №06/491 від 08 липня 2010 р.)
Рецензенти:
Піпа Б.Ф. – заслужений діяч науки і техніки України, доктор технічних наук, професор кафедри інженерної механіки Київського національного університету технології та дизайну;
Ковбаса В.П. – доктор технічних наук, професор, завідувач кафедри сільськогосподарського машинобудування та обладнання лісового комплексу Національного університету біоресурсів і природокористування України;
Сукач М.К. – доктор технічних наук, професор кафедри будівельних машин Київського національного технічного університету будівництва та архітектури.
К
С31
Isbn 978-966-640-295-3
Розроблено на основі робочої програми курсу «Деталі машин».
У навчальному посібнику стисло викладено матеріал курсу «Деталі машин» та подані тестові завдання. Матеріал поданий в достатній мірі для того, щоб дати відповіді на всі тестові завдання кожного з розділів.
Подано необхідний довідковий матеріал для розв’язування практичних задач.
Призначено для студентів денної та заочної форми навчання напрямів підготовки 6.050502 – Інженерна механіка, 6.070106 – Автомобільний транспорт.
УДК 621.81 (075)
ББК 344.44
© Вольченко О.І., Ловейкін В.С.,
Журавльов Д.Ю., Малик В.Я., 2010
isbn 978-966-640-295-3 © ІФНТУНГ, 2010
©
13
Зміст

Короткі методичні вказівки до вивчення матеріалу……………. Частина 1. Передачі……………………………………………………. Розділ 1. Загальні відомості про передачі……………………………. Розділ 2. Зубчасті передачі. Геометрія і кінематика циліндричних прямозубих передач……………………………………………………. Розділ 3. Зубчасті передачі. Основи розрахунку на контактну міцність і згин…………………………………………………………….. Розділ 4. Зубчасті передачі. Косозубі та шевронні колеса…………... Розділ 5. Конічні зубчасті передачі…………………………………… Розділ 6. Передача гвинт–гайка……………………………………….. Розділ 7. Черв’ячні передачі…………………………………………... Розділ 8. Фрикційні передачі і варіатори……………………………... Розділ 9. Пасові передачі………………………………………………. Розділ 10. Ланцюгові передачі…………………………………………
Частина 2. Вали та осі. Підшипники. Загальні відомості про редуктори. Муфти………………………………………………………. Розділ 11. Вали та осі………………………………............................... Розділ 12. Підшипники ковзання…………………................................ Розділ 13. Підшипники кочення……………………............................. Розділ 14. Загальні відомості про редуктори………………………… Розділ 15. Муфти……………………………………………………......
Частина 3. З’єднання. Загальні відомості про з’єднання………. Розділ 16. Роз’ємні з’єднання. Різьбові з’єднання…………………… Розділ 17. Шпонкові з’єднання………………………………………... Розділ 18. Шліцьові (зубчасті) з’єднання…………………………….. Розділ 19. Нероз’ємні з’єднання. Заклепкові з’єднання……………... Розділ 20. Зварні з’єднання………………………………………….....
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ….......................................
ДОДАТКИ………………………………………………………………...
Приклади змістовних модулів…………………............... |
5 8 8
19
29 40 49 54 57 67 78 92
102 102 112 119 130 142
154 154 167 170 179 184
195
196
231
|
Короткі методичні вказівки до вивчення матеріалу
Н авчальна дисципліна «Деталі машин» забезпечує базові знання основ розрахунку і конструювання деталей і складальних одиниць (вузлів) загального призначення.
При вивченні дисципліни «Деталі машин», в основному, використовують умовні позначення, які представлені у мірі викладення матеріалу.
Зубчасті передачі
u – передавальне число;
ω – кутова швидкість, с-1;
n – частота обертання, хв-1;
P – потужність, Вт, кВт;
η – коефіцієнт корисної дії (ККД);
T – обертовий момент, Нм, кНм;
Ft – колова сила, Н, кН;
Fr – радіальна сила, Н, кН;
Fa – осьова сила, Н, кН;
Fn – нормальна сила, Н, кН;
f – динамічний коефіцієнт тертя ковзання;
d, D – діаметр коліс (шківів), мм;
b – ширина коліс, мм;
аW – міжосьова відстань, мм;
т – модуль зачеплення, мм;
тп – нормальний модуль зачеплення, мм;
тt – торцевий модуль зачеплення, мм;
α – кут зачеплення, °;
pt – крок зубців (коловий), мм;
β – кут нахилу зубців, °;
de – зовнішній ділильний діаметр конічного колеса, мм;
d – середній ділильний діаметр конічного колеса, мм;
Re – зовнішня конусна відстань конічного колеса, мм;
R – середня конусна відстань конічного колеса, мм;
me – зовнішній коловий модуль зубців, мм;
m – середній модуль зубців, мм;
КH – коефіцієнт навантаження при розрахунку за контактними напруженнями;
KF – коефіцієнт навантаження при розрахунку на згин;
КH, KF – коефіцієнти навантаження при розрахунку за контактними напруженнями і на згин;
KHβ, KFβ – коефіцієнти нерівномірності розподілу навантаження по довжині контактної лінії;
KHV, KFV – коефіцієнти, що враховують внутрішню динаміку навантаження;
КHL, KFL – коефіцієнти довговічності, що враховують можливість підвищення допустимого напруження при короткотерміновій роботі;
σHlimb – границя контактної витривалості, МПа;
σFlimb – границя витривалості матеріалу при згині, МПа;
ψba – коефіцієнт ширини колеса по міжосьовій відстані;
ψbd – коефіцієнт ширини колеса за діаметром;
YF – коефіцієнт форми зубця при розрахунку на згин;
А – площа поперечного перерізу, мм2;
W – осьовий момент опору перерізу, мм3;
![]() – полярний
момент опору перерізу, мм3;
– полярний
момент опору перерізу, мм3;
![]() – допустиме
контактне напруження,
МПа;
– допустиме
контактне напруження,
МПа;
![]() – допустиме
напруження згину,
МПа;
– допустиме
напруження згину,
МПа;
σF – нормальне напруження згину, МПа;
![]() – напруження
стиску, МПа;
– напруження
стиску, МПа;
σH – контактне напруження, МПа;
E – модуль пружності, МПа;
Езв – зведений модуль пружності, МПа;
ρ – радіус кривини поверхні, мм;
ρзв – зведений радіус кривини, мм;
μ – коефіцієнт поперечної деформації (Пуассона);
qН – нормальне навантаження по довжині контактної лінії, Н/мм;
δ1, δ2 – кути ділильних конусів, °.
Черв’ячна передача
z1 – число заходів черв’яка;
q – число модулів в ділильному колі колеса (коефіцієнт діаметра);
γ – кут підйому гвинтової лінії черв’яка, °.
Пасові передачі
σ1, σ2 – напруження в перерізах паса при передачі навантаження, МПа;
α1, α2 – кути охоплення пасом шківів, °;
![]() – допустиме
корисне напруження, МПа;
– допустиме
корисне напруження, МПа;
k0 – зведене корисне напруження, МПа;
k – корисне напруження, МПа;
F0 – зусилля попереднього натяга, кН;
F1 – натяг набігаючої гілки паса, кН;
F2 – натяг збігаючої гілки паса, кН;
FV – зусилля в пасі від відцентрової сили, кН;
φ – коефіцієнт тяги;
Сθ; Сα; Cv; Cp – розрахункові коефіцієнти;
Сα – коефіцієнт, який враховує охоплення пасом шківа;
Cv – коефіцієнт, який враховує вплив сил інерції;
Cp – коефіцієнт, який враховує режим роботи передачі;
Сθ – коефіцієт, який враховує нахил лінії центрів шківів до горизонту;
ε – коефіцієнт ковзання в передачі.
Ланцюгова передача
t – крок ланцюга, мм;
рл – поточні питомі навантаження в шарнірі, Н/мм2, МПа;
![]() – допустиміі
питомі навантаження в шарнірі, МПа;
– допустиміі
питомі навантаження в шарнірі, МПа;
Ке – коефіцієнт експлуатації.
Фрикційна передача
Д – діапазон регулювання варіатора.
Зварні з’єднання
![]() ’
– допустиме
напруження розтягу для шва, МПа;
А’ –
розрахункова площа зварного шва, мм2;
’
– допустиме
напруження розтягу для шва, МПа;
А’ –
розрахункова площа зварного шва, мм2;
lш – довжина зварного шва, мм.
Шліцеве з’єднання
Азм – площа поверхні зминання, мм2;
l – довжина маточини колеса, мм;
z – число шлиців.
Ведучі деталі передач позначають непарними числами, ведені – парними. Інші позначення величин наводяться в тексті.
Під час вивчення матеріалу І розділу слід звернути увагу на наведені вимоги до мінімуму змісту і рівня підготовки студентів технічних спеціальностей. Знання основних питань курсу перевіряються за допомогою тестових завдань.
Рекомендується використовувати довідкові дані, наведені в додатку.
Частина 1. ПЕРЕДАЧІ
Розділ 1
ЗАГАЛЬНІ ВІДОМОСТІ ПРО ПЕРЕДАЧІ
Знати кінематичні і силові співвідношення в передавальних механізмах, формули для розрахунку передавального відношення, ККД, обертового моменту для всіх ступенів багатоступінчастого приводу.
Уміти вибрати тип механічної передачі для перетворення одного виду руху в інший, оцінити вибрану передачу, провести кінематичний та силовий розрахунки багатоступінчастої передачі.
Механічними передачами або передачами, називають пристрої, які передають енергію від двигуна до робочих органів машини з перетворенням швидкостей, сил або моментів, а інколи і характеру руху.
Основні причини застосування передач в машинах:
необхідні швидкості робочих органів машини часто не співпада-ють зі швидкостями стандартних двигунів;
швидкості робочого органу машини часто необхідно регулювати (змінювати) в процесі роботи;
більшість робочих органів машин повинні працювати при малих швидкостях і забезпечувати великі обертові моменти;
двигуни використовують для рівномірного обертового руху, а в машинах інколи потрібний поступальний рух зі змінними швидкос-тями.
Класифікація передач:
• за принципом передачі руху: передачі тертям і зачепленням; всередині кожної групи існують передачі безпосереднім контактом і передачі гнучким зв’язком;
• за взаємним розташуванням валів: передачі з паралельними валами (циліндричні), передачі з осями валів, що перетинаються (конічні), передачі з перехресними валами (черв’ячні, циліндричні з гвинтовим зубцем, гіпоїдні);
за характером передавального числа: зі сталим передавальним числом і з безступінчастою зміною передавального числа (варіатори).
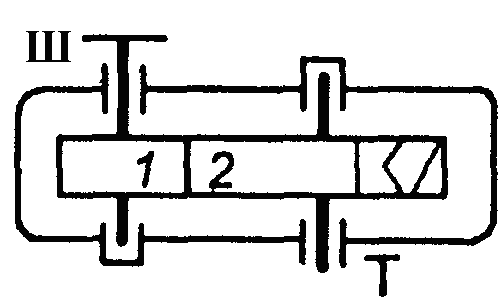
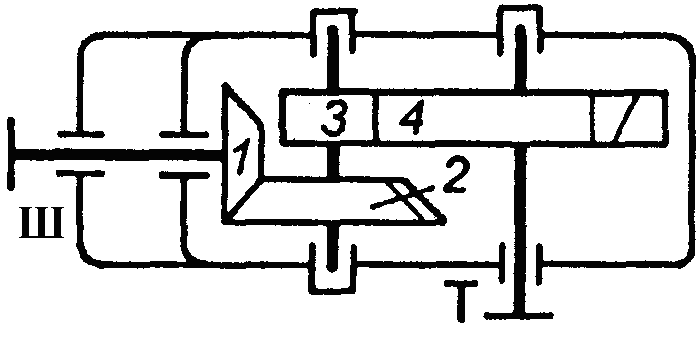
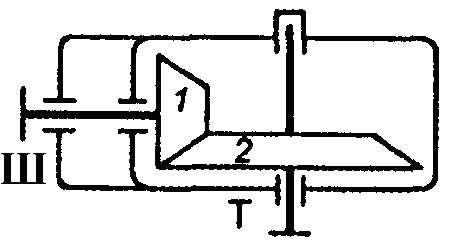
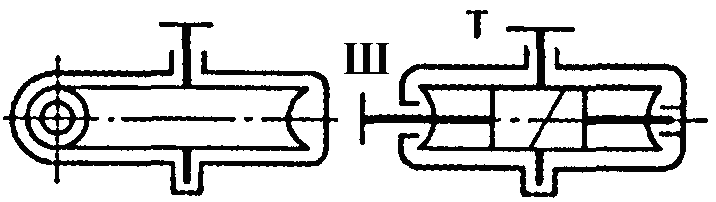
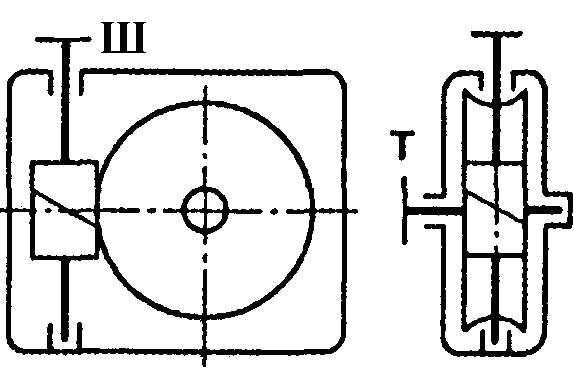
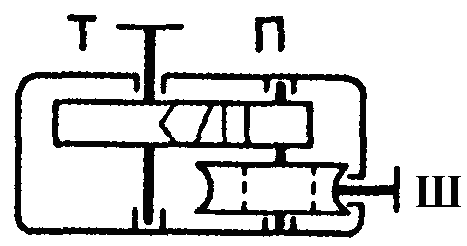
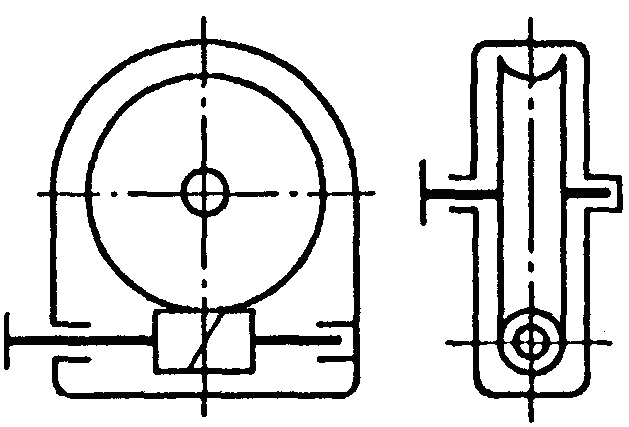
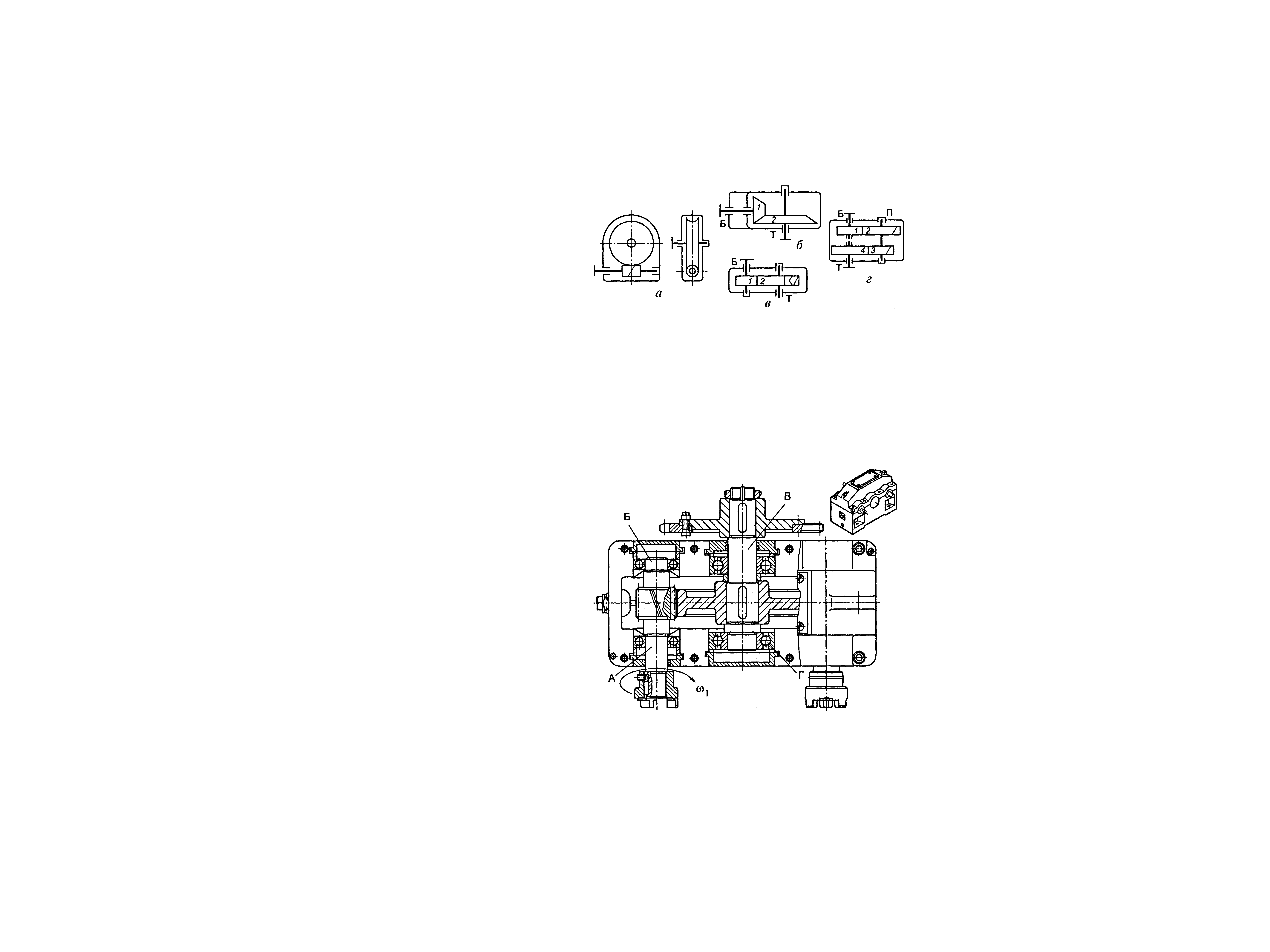
Фрикційні передачі (передачі тертям) – такі, в яких передача руху здійснюється силами тертя. Для створення тертя в контакті котків застосовують пружини і спеціальні натискні та натяжні пристрої. На рис. 1.1, а, б зображені фрикційні передачі безпосереднім контактом, на рис. 1.1, в варіатор – фрикційна передача з безступінчастим регулюванням швидкості за рахунок зміщення ролика 1, на рис. 1.1, з – передача гнучким зв’язком – пасова.
Передачі зачепленням «працюють» за рахунок зачеплення зубців і шарнірів ланцюга із зубцями зірочки. Тертя в даному випадку шкідливе, і більшість передач працюють із змащенням. Основна перевага передач із зачепленням – високий ККД, компактність і надійність.
На рис. 1.1, г, д зображені циліндрична і конічна зубчасті передачі, на рис. 1.1, е – черв’ячна (зубчасто-гвинтова передача), на рис. 1.1, ж – ланцюгова передача.
Кінематичні і силові співвідношення в передавальних механізмах
Кінематичні співвідношення в передачі можна розглянути за схемою циліндричної фрикційної передачі (див. рис. 1.1, а).
Колова
швидкість ведучого шківа:
![]() .
.
При
відсутності проковзування швидкість
ведучого і веденого шківів повинна
бути однаковою:
![]() ;
;
![]() ,
,
тоді
![]() ;
;
![]() .
.
Відношення кутової швидкості ведучого колеса до кутової швидкості веденого або частоти обертання ведучого колеса до частоти обертання веденого називається передавальним відношенням.
Для передач зачепленням використовують наступний вираз (оскільки діаметр колеса пропорційний його числу зубців):
![]() .
.
Зв’язок між потужностями на ведучій та веденій ланках можна отримати з відомих формул механіки:
![]() ;
;
![]() ;
;
![]() .
.
Відомо,
що
![]() ,
де Т
– обертовий момент; ω
– кутова швидкість.
Тоді
,
де Т
– обертовий момент; ω
– кутова швидкість.
Тоді
![]() ;
;
![]() .
.
У залежності від величини передавального відношення i передачі поділяються на: передачі зі сталим передавальним відношенням (і > 1; ω1 > ω2 – редуктори, понижуючі передачі; і < 1; ω1 < ω2 – мультиплікатори, підвищуючі передачі) і передачі з безступінчастим регулюванням швидкості.
Паралельно з поняттям передавального відношення і використовується поняття передавального числа u; для редукторів і = u.
У передачах з безступінчастим регулюванням швидкості (варіатори) передавальне відношення і – величина змінна, і їхньою характеристикою є діапазон регулювання:
![]() .
.
Якщо в механізмі необхідна значна зміна швидкості, застосовують багатоступінчасті передачі.
Ступінню вважають передачу однією парою коліс, одним комплектом пасів або одним ланцюгом.
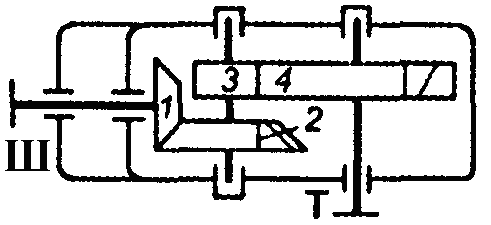
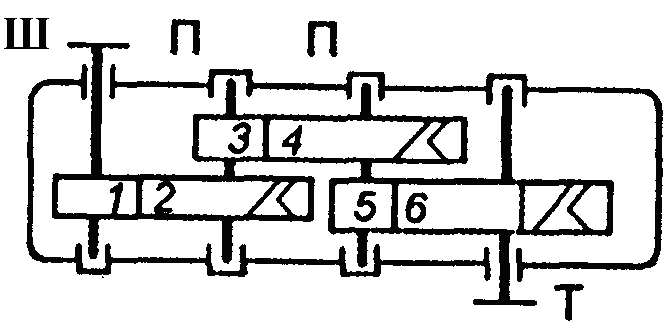
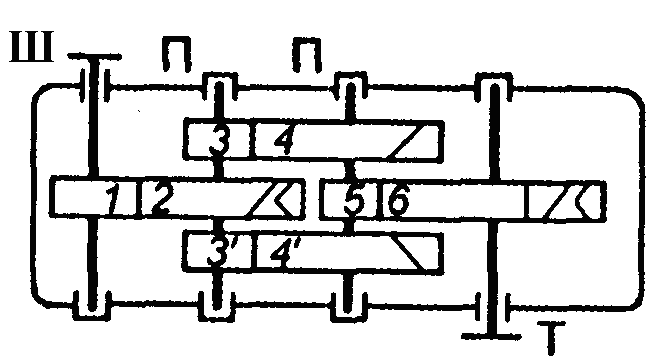
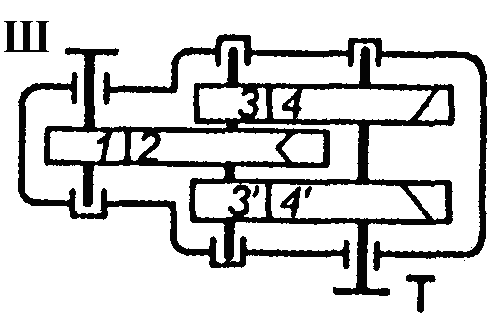
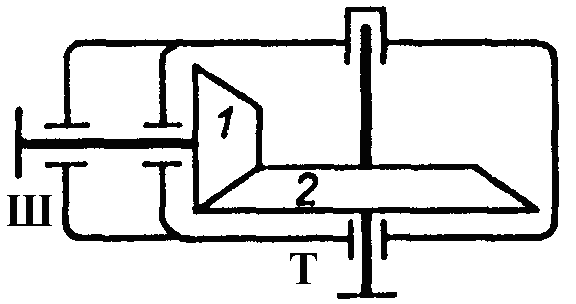
На рис. 1.2 зображено багатоступінчасті (двоступінчасті) передачі. Нумерація ступеней і коліс починається від двигуна.
Для багатоступінчастої передачі загальне передавальне число
![]() ,
,
де u1, u2, un – передавальні числа ступеней.
Рівень досконалості передачі характеризує коефіцієнт корисної дії, який для багатоступеневої передачі визначається за формулою:
загальний ККД передачі
![]() ,
,
де η1, η2, ηn – ККД ступенів.
![]() ,
,![]()
де ηп – ККД пасової передачі; ηц – ККД циліндричної зубчастої передачі; ηпідш – ККД підшипників.
Значення ККД вибирається в залежності від типу передачі.
9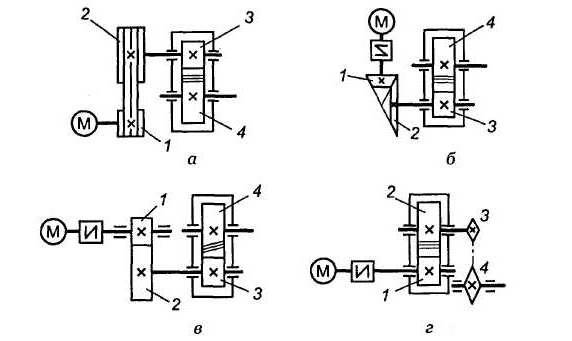
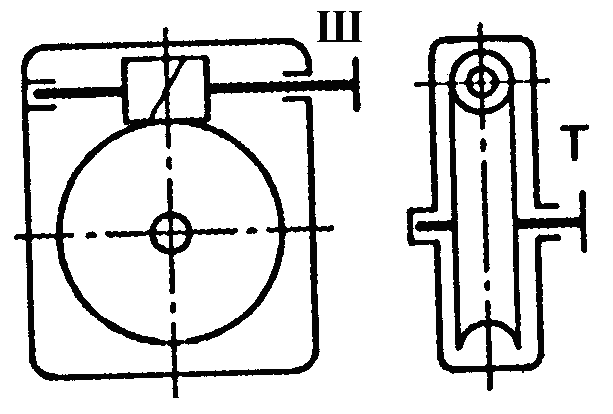
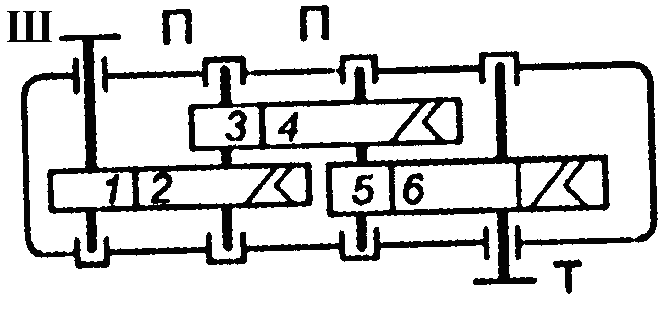
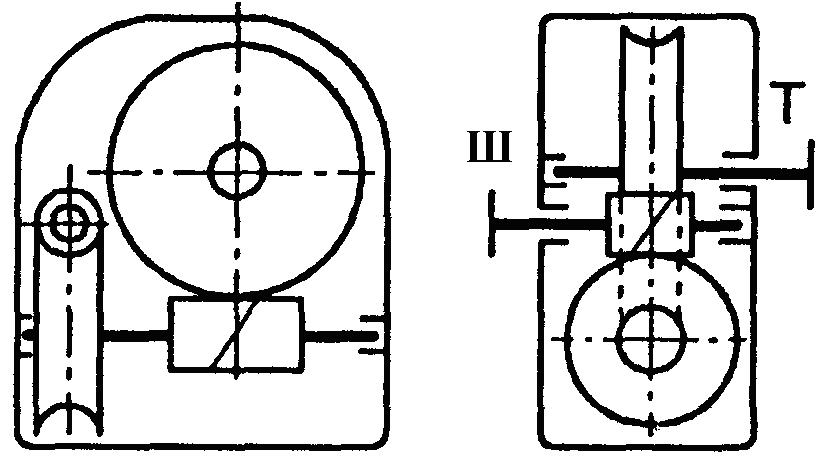
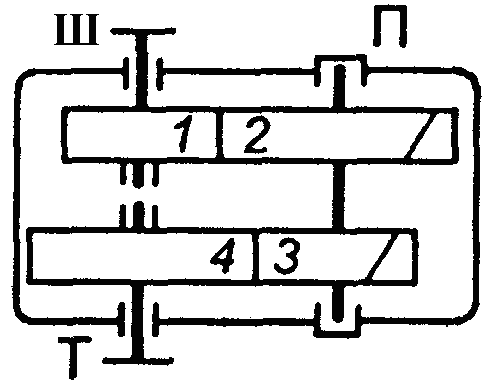
Рис. 1.2. Схема двоступеневих приводів: а – пасова передача і циліндричний редуктор; б – конічна передача і циліндричний редуктор;
в – двоступенева циліндрична передача; г – циліндричний редуктор і ланцюгова передача; 1, 3 – ведучі ланки; 2, 4 – ведені ланки
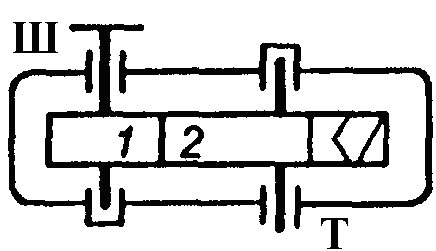
Для передачі, зображеної на рис. 1.3, можна записати:
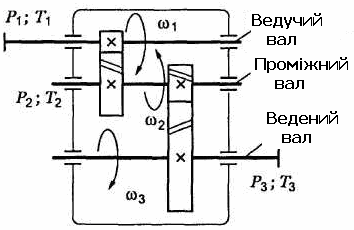
Рис. 1.3. Схема двоступеневої циліндричної передачі
![]() .
.
Кутові
швидкості валів:
![]() .
.
Обертові
моменти на валах:
![]() .
.
Якщо
врахувати, що
![]() ,
то
,
то
![]() ,
,
![]() .
.
У
розрахунках механічних передач
зустрічаються і такі параметри, як
колова швидкість та колова сила. Колова
швидкість
![]() –
це лінійна швидкість точок обертової
ланки передачі, розміщених на відстані
–
це лінійна швидкість точок обертової
ланки передачі, розміщених на відстані
![]() або
або
![]() від осі обертання:
від осі обертання:
![]() ,
,
де d1 і d2 – ділильні діаметри обертових ланок передачі.
Колова сила Ft – це сила, що діє на ланку передачі, спричиняючи її обертання або створюючи опір обертанню, і напрямлена по дотичній до траєкторії руху точки її прикладання:
![]() .
.
При
заданій передаваній потужності Р
(Вт) колова сила
![]() (Н)
обернено пропорційна коловій швидкості
V
(м/с):
(Н)
обернено пропорційна коловій швидкості
V
(м/с):
![]() .
.
Перейдемо до розгляду тестових завдань про механічні передачі, а також до вивчення частини: «Зубчасті передачі. Геометрія та кінематика циліндричних зубчастих передач».
Тема: Загальні відмості про передачі
1. Як зміниться потужність на вихідному валу передачі, якщо число зубців другого колеса z2 збільшити в два рази (див. рис. до завдання 10): а) збільшиться в 2 рази; б) зменшиться в 2 рази; в) не зміниться; г) збільшиться в 4 рази. |
2. Відомо, що передавальне відношення передачі 2,5. До якого типу передачі вона відноситься: а) мультиплікатор; б) редуктор; в) до обох типів; г) правильна відповідь не наведена. |
3. Як зміниться частота обертання вихідного вала привода при збільшенні числа зубців колеса в 2 рази (див. рис. до завдання 16): а) зросте в 2 рази; б) зменшиться в 2 рази; в) зросте в 4 рази; г) зменшиться в 4 рази. |
4. Відомо, що передавальне відношення передачі 10,5. До якого типу передачі вона відноситься: а) мультиплікатор; б) редуктор (черв’ячний); в) до обох типів; г) правильна відповідь не наведена. |
5. Котре з наведених відношень називається передавальним відношенням одноступеневої зубчастої передачі: а)
|
6. Яке призначення механічних передач: а) зменшувати втрати потужності; б) з’єднювати двигун з виконавчим механізмом; в) передавати механічну енергію з одночасним перетворенням параметрів руху; г) вирівнювати швидкості валів. |
7. Яке із наведених відношень називається передавальним відношенням одноступеневої передачі: а)
|
8. Відомо що передавальне відношення передачі 0,5. До якого типу передачі вона відноситься: а) мультиплікатор; б) редуктор; в) до обох типів; г) правильна відповідь не наведена. |
9. Як зміниться величина обертового моменту на вихідному валу передачі при збільшенні швидкості обертання вала двигуна в 1,5 рази, якщо його потужність є сталою: а) не зміниться; б) збільшиться в 3 раза; в) зменшиться в 1,5 раза; г) збільшиться в 1,5 раза. |
10. Серед наведених на схемах передач вибрати ланцюгову передачу та визначити її передавальне відношення, якщо: z1=18, z2=72, z3=17, z4=60, z5=1, z6= 36 , z7= 35, z8=88:
а) передача 1-2; 4; б) передача 3-4; 3,53; в) передача 5-6; 2,5; г) передача 7-8; 2,5. |
11. Визначити в циліндричній косозубій передачі обертовий момент на ведучому валу, якщо: потужність на вихідному валу передачі 6,6 кВт; кутові швидкості на вхідному та вихідному валах 60 та 15 с-1, відповідно; ККД = 0,96:
а)
440 Нм; б)110
Нм;
в)
1760 Нм; г)
115 Нм. |
12. Визначити передавальне відношення другої ступені передачі, якщо: ωвх=155 c-1; ωвих=20,5 с-1; z1=18; z2=54:
а)
7,51; б)
3; в)
2,52; г)
5,5.
|
13. Визначити необхідну потужність електродвигуна, якщо потужність на вихідному валу передачі 12,5 кВт; ККД пасової передачі 0,96; ККД черв’ячної передачі 0,82:
15
а)
12 кВт; б)
9,84 кВт; в)
15,24 кВт; г)
15,88 кВт. |
14. Для зображеної передачі визначити обертовий момент на веденому валу, якщо: Р1=5 кВт; ω1=157 с-1; ω2=62,8 с-1; ηц=0,97:
а)
31,87 Нм; б)
47,8 Нм;
в)
77,2 Нм; г)
79,7 Нм.
|
15. Для зображеної багатоступеневої передачі визначити загальне передавальне число, якщо: ω1=100 с-1; ω2=25 с-1; ω3=5 с-1:
а)
20; б)
4,5; в)
5; г)
5,5.
|
16. Визначити необхідну потужність електродвигуна, якщо: ηп=0,97; ηл=0,95; ηз=0,97; Рвих=10 кВт:
а)
8,94 кВт; б)
10,64 кВт;
в)
28,98кВт; г)
11,18 кВт.
|
17. Для циліндричної передачі визначити обертовий момент на вихідному валу, якщо: Р1=8 кВт; ω1= 40 с-1; ηц=0,97; u=4:
а)
800 Нм; б)
2200 Нм;
в)
776 Нм; г)
1940 Нм.
|
18. Для конічно-циліндричної передачі визначити загальне передавальне число, якщо: d1=50 мм; d2=200 мм; d3=35 мм; d4=70 мм:
а)
4; б)
6; в)
8; г)
10.
|
19. Визначити необхідну потужність електродвигуна, якщо: Рвих=5 кВт; η3=0,97; ηл=0,95:
а)
5,4 кВт; б)
9,6 кВт;
в)
6,4 кВт; г)
4,6 кВт.
|
20. Для зображеної передачі визначити обертовий момент на ведучому валу, якщо: Р1 = 8,5 кВт; ω2= 12 с-1; u=2; ηц = 0,96:
а)
708,5 Нм; б)
301,2 Нм;
в)
368,9 Нм; г)
7,02 Нм.
|
2
а )
4,5; б)
12,35; в)
2,02; г)
5.
|
22. Визначити необхідну потужність електродвигуна лебідки, якщо: швидкість піднімання вантажу 4 м/с; вага вантажу 1000 Н; ККД барабана 0,9; ККД циліндричної передачі 0,98:
а)
3,53кВт; б)
4,53 кВт;
в)
2,15 кВт;
г) 7,32 кВт.
|
23. Для наведеної передачі визначити обертовий момент на веденому валу, якщо: Р1 = 6 кВт; ω2 = 20 с-1; ηц=0,97; u = 2,5:
а)
116 Нм; б)
291 Нм;
в)
382 Нм; г)
464 Нм. |
24. Для багатоступеневої передачі визначити загальне передавальне число, якщо: z1=20; z2=80; z3=30; z4=75; z5 = 40; z6= 200:
а)
25; б)
50; в)
20; г)
75.
|
25. Визначити необхідну потужність електродвигуна, якщо: Рвих= 8 кВт; ηз= 0,97; ηч=0,82:
а)
6,36 кВт; б)
8,82 кВт;
в)
10 кВт; г)
12,3 кВт. |
Розділ 2
ЗУБЧАСТІ ПЕРЕДАЧІ. ГЕОМЕТРІЯ
І КІНЕМАТИКА ЦИЛІНДРИЧНИХ
ПРЯМОЗУБИХ ПЕРЕДАЧ
Знати характеристики евольвентного зачеплення;формули геометричного розрахунку циліндричних прямозубих коліс; уміти ними користуватись.
У зубчастих передачах рух передається за рахунок зачеплення пари зубчастих коліс. Ведуче колесо пари зачеплення називається шестірнею, ведене – колесом.
Класифікація зубчастих передач
Зубчасті передачі застосовують при будь-якому розташуванні осей коліс. При паралельному розташуванні осей коліс використовують циліндричну передачу, при осях, що перетинаються – конічну передачу, при осях валів, що схрещуються – гвинтові, гіпоїдні, спіроїдні (рис. 2.1).
Зубчасті передачі виконують в основному закритими (які працюють в корпусі із мастилом).
Відкриті передачі, які працюють на повітрі без мастила, зазвичай відрізняються великими розмірами. Для них характерне пришвидшене зношування взаємодіючих пар зачеплення.
У залежності від розташування зубців на колесі розрізняють прямозубі, косозубі, шевронні колеса і колеса з круговими зубцями (рис. 2.1, а–в, и, к).
Гвинтові передачі (зубчасті циліндричні передачі з гвинтовим зубцем) через підвищене ковзання і низької навантажувальної здатності застосовують обмежено (рис. 2.1, е).
Для перетворення обертового руху в поступальний застосовують передачу шестірня – рейка (рис. 2.1, г).
У залежності від форми профіля зубців передачі поділяються на передачі з евольвентними зубцями і зубцями, які окреслені дугами кола (передача Новікова).
У залежності від взаємного положення коліс розрізняють передачу із зовнішнім (рис. 2.1, а) та внутрішнім (рис. 2.1, д) зачепленням.


Геометрія і кінематика зубчастих коліс
Поверхні взаємодіючих зубців повинні забезпечити сталість передавального числа. Профілі зубців повинні відповідати вимогам, випливаючим з основної теореми зачеплення: загальна нормаль, проведена через точку дотику профілів, ділить відстань між центрами О1О2 на частини обернено пропорційні до кутових швидкостей (рис. 2.2).
Практичне застосування отримало евольвентне зачеплення завдяки технологічності і досить високої несучої здатності. Робочими профілями зубців коліс служить евольвента. Кожне евольвентне колесо нарізане так, що може зчіплятись з відповідними колесами, що мають будь-яке число зубців.
Усі геометричні параметри зубчастих передач стандартизовані.
З кінематичної точки зору зачеплення зубчастих коліс еквівалентне коченню без ковзання двох кіл з діаметрами О2П і О1П.
В якості основного параметру зубчастих коліс прийнято модуль.
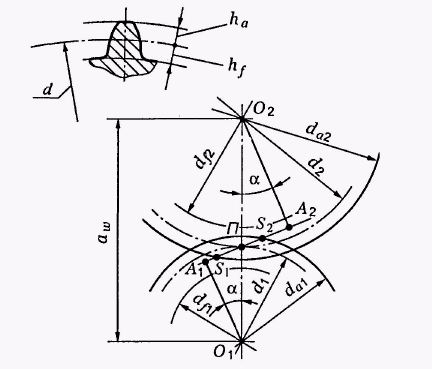
Рис. 2.2. Геометрія циліндричної передачі: П – полюс зачеплення;
А1А2 – лінія зачеплення; S1S2 – довжина активної лінії зачеплення; α – кут зачеплення; aw – міжосьова відстань; d1, d2 – діаметри ділильних кіл;
ha, hf – висота головки і ніжки зубця, відповідно; df1, df2 – діаметри кіл западин; da1, da2 – діаметри кіл вершин
Модуль – розрахункова величина, рівна відношенню колового кроку зубців рt, по ділильному колу до числа π:
![]() .
.
Крок зачеплення – відстань між двома однойменними профілями сусідніх зубців по ділильному колу. Кроки зчіпних зубців повинні бути рівні.
Ділильне коло ділить зубець на дві частини: головку і ніжку.
Геометрія циліндричних коліс визначається декількома концентричними колами.
Початкові кола – це спряжені кола двох зчіпних коліс. Їх радіуси рівні ОП1 і ОП2. Початкові кола відносяться тільки до зачеплення пари коліс. При зміні міжосьової відстані О1О2 діаметри початкових кіл також міняються.
Ділильне коло належить кожному окремо взятому колесу. Ділильне коло є початковим при зубонарізанні, при зачепленні колеса з виробничою рейкою. У більшості зубчастих передач ділильні кола збігаються з початковими:
![]() .
.
Основні параметри зубчастого колеса виражаються через модуль m.
Діаметр
ділильного кола
![]() де z
– число зубців.
де z
– число зубців.
Діаметр
кіл виступів
![]() .
.
Діаметр
кіл западин
![]() .
.
Висота головки зубця ha = m.
Висота ніжки зубця hf = 1,25m.
Для забезпечення взаємозамінюваності модулі зубців циліндричних коліс стандартизовані (див. табл. Д1).
При передачі руху зубці коліс зачеплюються на лінії А1А2 (лінія зачеплення). Лінія зачеплення утворює з дотичною, проведеною в точці дотику П (полюс зачеплення), кут зачеплення α; для циліндричних коліс α = 20°.
Лінія А1А2 – загальна нормаль до поверхонь зубців в точці дотику. Практично зачеплення відбувається між точками перетину лінії зачеплення з колами вершин коліс S1S2.
Основним геометричним параметром циліндричної передачі є міжосьова відстань:
![]() .
.
Міжосьові відстані і передавальні числа циліндричних зубчастих коліс стандартизовані (див. табл. Д2, Д3).
Безперервність роботи передачі забезпечена, якщо наступна пара зубців входить в зачеплення до виходу попередньої (перекриття). Коефіцієнт торцьового перекриття εα – відношення довжини активної лінії зачеплення до основного кроку, εα > 1.
Методи нарізання зубців
Метод обкатування – точний, високопродуктивний і найбільш поширений метод. Процес нарізання зубців повторює процес зачеплення двох коліс або колеса з рейкою. Одне з коліс або рейка мають ріжучі закраїни і є ріжучим інструментом, який зветься виробничим колесом.
Заготовка обертається, інструмент переміщується вздовж заготовки. Нарізання може відбуватись інструментальною рейкою, довбачем або черв’ячною модульною фрезою.
При нарізанні зубців черв’ячною фрезою (рис. 2.3, а) заготовка і фреза обертаються навколо своїх осей, забезпечуючи безперервність процеса. Одним і тим же інструментом можна нарізати колеса даного модуля з різним числом зубців (рис. 2.3, а, б).
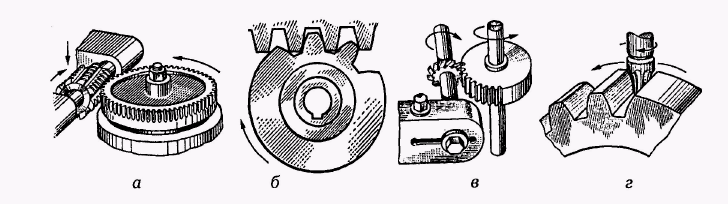
Рис. 2.3. Види зубонарізання: а, б – методом обкатування; в, г – методом копіювання
Метод копіювання характерний тим, що ріжучий інструмент відповідає профілю западини зубця колеса. Після нарізання однієї западини заготовку повертають на величину одного кроку і операцію повторюють. Із зміною числа зубців змінюється форма западини, тому для кожного модуля і числа зубців потрібно мати окрему фрезу. Нарізання зубців методом копіювання – недостатньо точний і меншвиробничий метод, який застосовується в дрібносерійному виробництві. Копіювання відбувається дисковою (рис. 2.3, в) або кінцевою (рис. 2.3, г) фрезами.
Поняття про зубчасті колеса із зміщенням
При заданому модулі зміна числа зубців призводить до зміни форми зубця. Із зменшенням числа зубців колеса товщина зубця в основі зменшується, і при деякому мінімальному значенні z з’являється підрізання зубця ріжучою кромкою інструмента.
Зміщення зубців (модифікацію) застосовують:
для усунення підрізання зубців при z < zmin;
для підвищення міцності зубців шляхом збільшення їх товщини;
для збільшення радіуса в точці дотику (при цьому збільшується контактна міцність);
для отримання заданої міжосьової відстані.
При нарізанні коліс із зміщенням інструмент зсувається від центра заготовки (позитивний зсув) або до центра (негативний зсув).
Модифікація буває висотною і кутовою.
При
висотній
модифікації
колесо і шестірню виготовляють з
протилежним зміщенням. Шестірню
виготовляють з позитивним зміщенням,
колесо – з негативним. Сумарний
коефіцієнт зміщення
![]() ,
де x1,
x2
– коефіцієнти зміщення шестірні і
колеса, відповідно. Міжосьова відстань
і кут зачеплення не змінюються.
,
де x1,
x2
– коефіцієнти зміщення шестірні і
колеса, відповідно. Міжосьова відстань
і кут зачеплення не змінюються.
При кутовій модифікації сумарний коефіцієнт зміщення відмінний від нуля, а міжосьова відстань і кут зачеплення змінюються.
При малому z інструменту надають зміщення χm.
При α = 20° мінімальне число зубців 13 < zmin < 17.
Перейдемо до розгляду тестових завдань до цієї теми, а також до вивчення наступного розділу: «Зубчасті передачі. Основи розрахунку на контактну міцність і згин».
Тема: Зубчасті передачі. Геометрія та кінематика циліндричних прямозубих передач
1. Що таке лінія зачеплення: а) лінія, що окреслює профіль зубця; б) лінія, що проходить через центри коліс; в) загальна нормаль до профілей зубців у точці дотику; г) дотична до профілю зубця в точці дотику. |
2. Знайти формулу для визначення модуля зубців: а)
|
3. Котрі значення модулів зубців відповідають стандарту: а) 1,9 мм; б) 2,4 мм; в) 4 мм; г) 21 мм. |
4. Вкажіть основні переваги евольвентних коліс: а) простота конструкції; б) сталість передавального відношення; в) безшумність роботи; г) вимоги точності при складанні. |
5. Який кут зачеплення циліндричних коліс: а) 30°; б) 18°; в) 20°; г) 14°. |
6. Що таке ділильний коловий крок зубців: а) відстань між профілями сусідніх зубців; б) відстань між одноіменними профілями сусідніх зубців по ділильному колу; в) ширина зубця по ділильному колу; г) довжина дуги ділильного кола між сусідніми зубцями. |
7. Вказати формулу для визначення діаметра кола виступів циліндричного зубчастого колеса:
а)
в)
|
8. Які параметри циліндричної зубчастої передачі є стандартизовані: а) u, m, aw, α; б) z, u, m, aw; в) u, m, d1, α; г) m, aw, z1, d1. |
9
а)
б)
в)
г)
|
10. Який кут називають кутом зачеплення:
а)
геометричне місце точок дотику
профілів зубців;
б)
кут між лінією центрів і лінією
зачеплення;
в)
кут між лінією зачеплення і прямою,
перпендикулярній
лінії центрів;
г)
кут між лінією зубця і твірною циліндра
колеса.
|
11. Вибрати формулу для визначення діаметра ділильного кола циліндричної зубчастої передачі: а)
;
б)
|
12. Яка основна перевага конічних зубчастих передач:
а)
простота виготовлення і монтажу; б)
малі габаритні розміри і вага;
в)
рівномірність розподілу наванта-ження
в зачепленні;
г)
можливість з’єднання валів з ося-ми,
що перетинаються. |
13. Що називають коефіцієнтом торцевого перекриття:
а)
відношення кута зачеплення до числа
зубців;
б)
відношення кута перекриття до
кута
зачеплення;
в)
відношення швидкості на вході в
передачу
до швидкості на виході;
г)
відношення довжини активних
ліній
зачеплення
до основного кроку.
|
14. Вказати формулу для розрахунку міжосьової відстані передачі:
а)
в)
|
1
а)
вісі коліс перетинаються;
б)
складність виготовлення; монтажу й
обслуговування;
в)
невисока точність передачі;
г)
нестале передавальне відношення.
|
16. Визначити aw, якщо: d1= 64 мм, Z2= 80, m = 2 мм:
а)
78 мм; б)
224 мм;
в)
112 мм;
г) 160 мм.
|
17. Визначити зовнішню конусну відстань прямозубої конічної передачі, якщо: зовнішній коловий модуль зубців 4 мм; число зубців шестірні 13; передавальне число передачі 3,08:
а)
52 мм; б)
84 мм;
в)
73,9 мм; г)
156 мм.
|
18. Визначити модуль зубця колеса, якщо коловий крок 12,56 мм: а) 12,5 мм; б) 6 мм; в) 2,5 мм; г) 4 мм. |
19. Розрахувати передавальне відношення передачі, якщо: аW=160 мм, d1=80 мм:
а)
2; б)
2,5; в)
3; г)
4. |
20. Визначити
передавальне відношення конічної
прямозубої передачі, якщо:
а)
0,4; б)
2; в)
2,5; г)
3,5.
|
21. Визначити число зубців ведучої шестірні, якщо: передавальне відношення пари зубчастих коліс 3,15; модуль зачеплення 2,5 мм; міжосьова відстань 120 мм: а) 17; б) 18; в) 23; г) 26. |
22. Розрахувати крок зубців, якщо висота зубця колеса h=6,75 мм: а) 3 мм; б) 6,75 мм; в) 9,42 мм; г) 13,5 мм. |
23. Визначити міжосьову відстань прямозубої циліндричної передачі, якщо: діаметр ділильного кола шестірні 72 мм; число зубців колеса 90; модуль передачі 4 мм: а) 108 мм; б) 216 мм; в) 360 мм; г) 432 мм. |
24. Визначити діаметри кіл виступів зубчастих коліс передачі, якщо: висота зубця колеса 5,625 мм; число зубців шестірні 18; передавальне відношення передачі 2,5: а) 38,75 мм; 106,26 мм; б) 45 мм; 112,5 мм; в) 50 мм; 117,5 мм; г) 50 мм; 167,5 мм. |
25. Визначити передавальне відношення передачі, якщо: діаметр ділильного кола шестірні 59,5 мм, модуль зубця 3,5 мм, число зубців колеса 68: а) 3,15; б) 4; в) 5; г) 6,3. |
Розділ 3
ЗУБЧАСТІ ПЕРЕДАЧІ. ОСНОВИ РОЗРАХУНКУ
НА КОНТАКТНУ МІЦНІСТЬ І ЗГИН
Знати про види руйнування, критерії працездатності, матеріали, допустимі напруження зубчастих передач, геометричні, кінематичні і силові співвідношення циліндричних зубчастих передач; формули для розрахунку зусиль в зачепленні; формули для розрахунку прямозубих передач на контактну міцність і згин; позначення, фізичний зміст і порядок визначення всіх коефіцієнтів, які входять у формули: коефіцієнтів навантаження, коефіцієнта ширини колеса, коефіцієнта форми зубця, допустимих напружень.
Матеріали
Основні вимоги до матеріалів:
міцність поверхневого шару і високий опір стиранню;
достатня міцність при згині;
оброблюваність, можливість отримання достатньої точності і чистоти поверхні.
Основним матеріалом зубчастих коліс є сталь, використовують також чавун і пластмасу. Для зміцнення поверхні зубців застосовують термообробку. Твердість поверхні має бути такою, щоб отримати колеса необхідної точності.
Найбільшого поширення набули вуглецеві сталі 35; 40; 50; 50Г. Застосовують леговані сталі 40Х; 45ХН. Вуглецеві сталі піддають нормалізації та поліпшенню, твердість поверхні 300...320 НВ.
Леговані сталі гартують, інколи застосовують поверхневе гартування, цементацію, азотування (НВ > 350).
Застосування високотвердих матеріалів зменшує габаритні розміри передачі і збільшує її довговічність. Проте колеса з таких матеріалів потребують підвищеної точності виготовлення і монтажу, а обробку різанням проводять до термообробки. Рекомендації щодо вибору матеріалів і термообробки наводяться в табл. Д4.
Більші зубчасті колеса з пластмаси застосовують для забезпечення безшумної роботи. Шестірня з пластмаси працює з колесом із сталі; навантажувальна здатність таких передач невисока.
Причини виходу з ладу і критерії працездатності передачі
Для зубчастих передач основними причинами виходу з ладу є пошкодження поверхні: втомне викришування для закритих передач, працюючих в мастилі, і зношування поверхні для відкритих передач.
У високонавантажених і високошвидкісних передачах може виникнути заїдання – зварювання частинок металу з наступним відривом від менш міцнішої поверхні. Нарости, які при цьому утворилися, задирають робочі поверхні.
Усі види пошкоджень поверхні пов’язані з нормальними напруженнями в контакті зубців σH, які називаються контактними напруженнями.
Основними критеріями працездатності зубців є контактна міцність і міцність при згині.
Сили в зачепленні прямозубих коліс
Розподілене навантаження на площі контакту прийнято представляти у вигляді зосередженої сили, прикладеної в точці зачеплення і направленої по лінії зачеплення (рис. 3.1).
Для розрахунків силу Fn розкладають на складові:
![]() ,
,
де Ft
– колова
сила,
![]() ,
,
Fr
– радіальна
сила,
![]() .
.
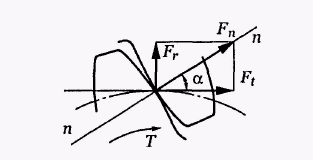
Рис. 3.1. Сили в зачепленні прямозубого колеса
Розрахунок на контактну міцність зубчастих передач
Розрахунок
на контактну міцність зводиться до
перевірки умови
![]() .
.
Розміри зубчастої передачі визначають із розрахунку (проектний розрахунок) за контактними напруженнями (рис. 3.2). За основу приймають формулу Герца для контакта циліндричних поверхонь. Після відповідних перетворень і введення різних коефіцієнтів, що враховують особливості геометрії зубця і характер діючого навантаження, отримують формулу для визначення основного геометричного параметра зубчастої циліндричної передачі – міжосьової відстані, мм:
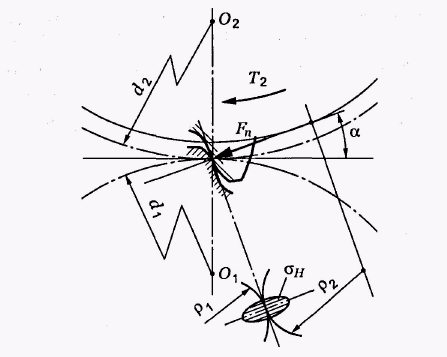
Рис. 3.2. Контактні напруження в зачепленні зубців при передачі обертового моменту
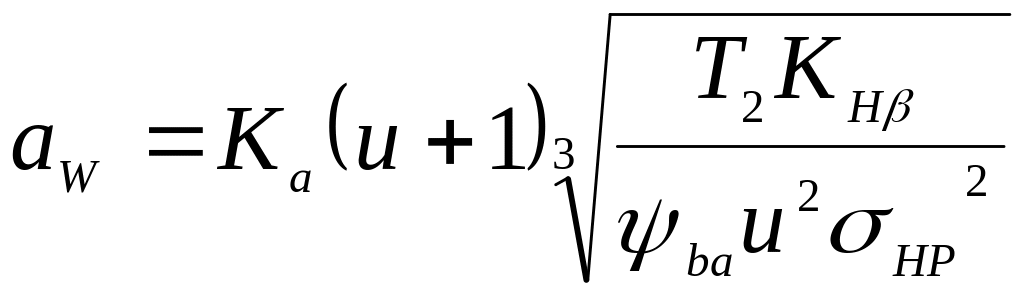 ,
,
де Т2 – обертовий момент, на веденому валу, Н · мм;
u – передавальне число;
K
30
![]() – коефіцієнт
ширини колеса по міжосьовій
відстані;
– коефіцієнт
ширини колеса по міжосьовій
відстані;
ψba
= 0,2…0,5;
значення ψba
можна визначити за формулою
![]() ,
,
де
![]() і
вибирається за табл. Д5;
і
вибирається за табл. Д5;
![]() – допустиме
контактне
напруження;
– допустиме
контактне
напруження;
де
![]() –
коефіцієнт довговічності;
–
коефіцієнт довговічності;
σH limb – межа контактної витривалості;
![]() – допустимий
коефіцієнт безпеки.
– допустимий
коефіцієнт безпеки.
Дослідження
показали, що границя контактної
витривалості σHlimb
і базове число циклів навантажень NHO
в основному залежать від твердості
робочої поверхні зубців; коефіцієнт
KHL
враховує можливість підвищення
допустимого напруження, при
короткотерміновому навантаженні;
σHlimb
визначається для вибраного матеріалу
з таблиці;![]() –
розрахункове число циклів навантаження
зубців
–
розрахункове число циклів навантаження
зубців
![]() ;
Lh
– повний ресурс, год. За розрахункове
число циклів навантажень приймається
менше із допустимих значень для шестірні
і колеса.
;
Lh
– повний ресурс, год. За розрахункове
число циклів навантажень приймається
менше із допустимих значень для шестірні
і колеса.
Отримане значення міжосьової відстані порівнюють зі стандартним значенням, вибираючи найближче. Для нестандартних редукторів отримане значення округлюють за рядом переважаючих чисел (табл. Д7).
Визначають всі геометричні параметри передачі. Отриману передачу перевіряють на міцність за формулою:
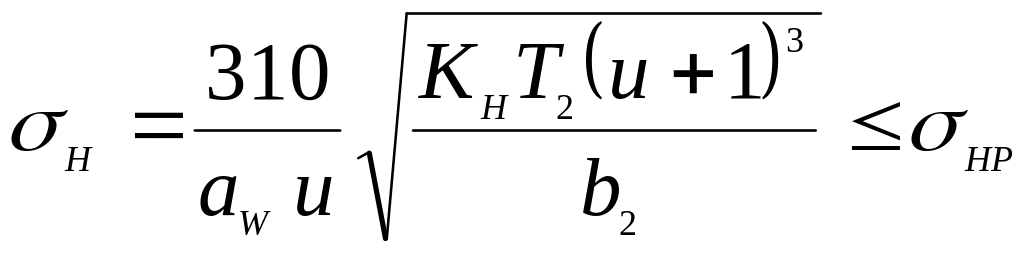 ,
,
де
![]() – коефіцієнт навантаження;
– коефіцієнт навантаження;
![]() .
.
Злам зубця. Розрахунок зубчастих коліс на згин
Злам зубців пов’язаний з напруженнями згину. Частіше спостерігається виламування зубців унаслідок перевантажень і втоми матеріалу від тривало діючих змінних навантажень.
Розрахунок
на згин зводиться до перевірки умови
![]() .
.
При розрахунку на згин вважають, що в зачепленні знаходиться одна пара зубців. Зубець розглядають як консольну балку з силою Fn, яка прикладена до його вершини (рис. 3.3). Під дією сили, зубець стискається і згинається.
При розрахунку враховують сумарне напруження на розтягнутій стороні. При отриманні формули використовують коефіцієнти, що враховують особливість форми зубця і характер діючого навантаження. Остаточна формула для перевірного розрахунку на згин така:
![]() ,
,
де YF2 – коефіцієнт форми зубця, який залежить від числа зубців (табл. Д6);
Ft – колова сила;
![]() – допустиме
напруження
згину,
– допустиме
напруження
згину,
![]() ,
де
,
де
σF limb – границя витривалості зубців при згині;
KFC – коефіцієнт, що враховує двостороннє прикладання навантаження:
![]() ,
NFO
=
4·106.
,
NFO
=
4·106.
Зубець
шестірні в основі тонший, ніж у колеса,
тому для забезпечення
однакової міцності шестірню виконують
з міцнішого матеріалу, ніж
колесо. Для забезпечення рівної згинальної
міцності зубців шестірні і колеса
бажано, щоб
![]() .
.
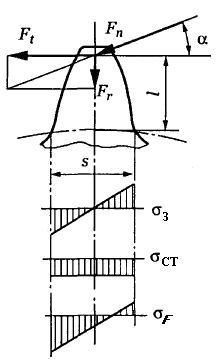
Рис. 3.3. Епюри визначення напружень згину у перерізі зубця
Розрахунок ведуть
для колеса, в якого
![]() менше.
менше.
Таблиця 3.1.
Вибір границь витривалості робочих поверхонь зубців, МПа:
-
Середня твердість поверхні
σH limb
σF limb
Не більше 350 HB
2 НВ + 70
1,75 НВ
38...50 HRC
17 HRC + 200
500...700
Більше 56 HRC
23 HRC
700...950
Коефіцієнти при розрахунку зубчастих коліс на контактну міцність і згин
КH, KF – коефіцієнти навантаження при розрахунку за контактними напруженнями і на згин.
KHβ, KFβ – коефіцієнти нерівномірності розподілу навантаження по довжині контактної лінії.
KHV, KFV – коефіцієнти, що враховують внутрішню динаміку навантаження.
КHL, KFL – коефіцієнти довговічності, що враховують можливість підвищення допустимого напруження, при короткотерміновій роботі.
![]() ,
,
![]() – допустимі коефіцієнти безпеки,
= 1,1...1,3;
– допустимі коефіцієнти безпеки,
= 1,1...1,3;
![]() .
.
При нереверсивному навантаженні KFC = 1; при двосторонньому навантаженні KFC =0,7...0,8.
Розрахунок відкритих передач
Відкриті передачі працюють без корпуса і мастила, як правило, при малих швидкостях, мають інтенсивне абразивне зношування. Колеса виконують прямозубими і вузькими, з матеріалу з твердістю 250...280 HВ. Проектний розрахунок відкритих передач проводиться за контактними напруженнями з перевіркою на згин аналогічно до розрахунку закритих передач.
Таким чином, після викладення теоретичного матеріалу з даної теми, перейдемо до розгляду тестових питань для закріплення набутих знань, а також до вивчення нової теми: «Зубчасті передачі. Основи розрахунку на контактну міцність і згин».
34
34
Тема: Зубчасті передачі. Основи розрахунку на контактну міцність і згин
1
а)
значне зношування робочої поверхні
зубця;
б)
злам зубця;
в)
викришування робочої поверхні зубця;
г)
заклинювання підшипників.
|
2. Вибрати формулу для проектного розрахунку циліндричної прямозубої передачі:
а)
в)
|
3. Що враховує коефіцієнт Кнв, який входить в залежність для розрахунку зубчастих коліс: а) поштовхи й удари при роботі передачі; б) похибку основного кроку зубців; в) концентрацію навантаження в результаті перекосу валів; г) зміну режиму навантаження при роботі. |
4. Для якого
колеса необхідно виконати перевірку
на згин, якщо коефіцієнти форми
зубця YF1=4,27,
YF2=3,6;
допустимі
напруження згину
а) перевірити колесо 1; б) перевірити колесо 2; в) перевірка не проводиться; г) перевіряють обидва колеса. |
5. Яка основна причина виходу з ладу відкритих зубчастих передач: а) втомні мікротріщини; б) зношування робочої поверхні зубця; в) викришування робочої поверхні зубця; г) перекіс валів. |
6. Вказати формулу для перевірки циліндричної зубчастої передачі на згин:
а)
в) |
7. Що враховують коефіцієнти КHV і КFV які входять у формулу для розрахунку зубчастих передач: а) зміну режиму навантаження при роботі; б) динамічні навантаження через неточність виготовлення коліс; в) концентрацію навантаження із-за перекосу вала; г) взаємне перекриття. |
8. За якою із механічних характеристик визначають допустиме контактне напруження зубчастих коліс: а) σТ; б) σВ; в) δ,%; г) HB. |
9. Із наведених нижче графіків вибрати графік зміни контактних напружень в точці зачеплення зубчастих коліс:
а
б
в
г
а) а; б) б; в) в; г) г. |
10. Як називається величина q в залежності для визначення максимальних нормальних напружень, які виникають в контакті двох циліндричних поверхонь із металу
а) нормальне навантаження по довжині контактної лінії; б) зведене навантаження; в) тиск на зубець; г) колова сила по довжині контактної лінії. |
11. За якою залежністю визначається напруження при розрахунку зубчастих коліс на згин:
а)
в)
|
12. Від яких параметрів залежить коефіцієнт форми зубця YF у виразі для розрахунку зубчастих коліс на згин: а) від u; б) від m; в) від z; г) від точності передачі. |
13. Зображені основні види руйнування зубців. Назвіть вид руйнування в:
а
б
в
г
а) злам зубця; б) втомне викришування робочих поверхонь зубців; в) зношування зубців; г) заїдання зубців. |
14. Підібрати матеріал для колеса із запропонованих марок сталі, якщо: матеріал шестірні – сталь 45 Х покращена, твердість 230…280 НВ: а) 40 ХН (поліпшена), 230…300 НВ; б) 40 ХН (гартування), 48…54 HRС; в) 45 (нормалізація), 170…217 НВ; г) потрібна марка не вказана. |
15. Від яких
особливостей передачі залежить вибір
коефіцієнта
а) розташування колеса на валу і твердості; б) призначення передачі і границі міцності; в) розташування передачі в просторі; г) діаметра колеса. |
16. Від яких параметрів та як залежить коефіцієнт форми зубця YF: а) YF – сталий коефіцієнт; б) YF збільшується з ростом числа зубців z; в) YF зменшується з ростом числа зубців z; г) YF зменшується з ростом модуля m. |
17. З якими напруженнями при роботі передачі зв’язаний злам зубців: а) з напруженням стиску; б) з напруженням зсуву; в) з контактним напруженням; г) з напруженням згину. |
18. Із наведених графіків вибрати графік напруження згину в зубці при роботі передачі:
а
б
в
г
а) а; б) б; в) в; г) г. |
19. Вказати формулу для перевірного розрахунку циліндричної передачі за контактними напруженнями: а) |
20. Як впливає підвищення твердості поверхні на контактну міцність зубчастих коліс: а)
не впливає; б)
підвищується
|
21. Визначити нормальну силу в зачепленні зубців коліс Fn, якщо: обертовий момент на валу циліндричної прямозубої передачі 120 Нм, діаметр ділильного кола колеса 0,2 м (sin20º=0,342; cos20º=0,94; tg20º=0,364): а) 1277 Н; б) 1754 Н; в) 3296 Н; г) 3509 Н. |
22. Визначити радіальне навантаження Fr в циліндричній прямозубій шестірні, ділильний діаметр якої 0,125 м, якщо: потужність на ведучому валу 4 кВт, кутова швидкість 50 с-1 (sin20º=0,342; cos20º=0,94; tg20º=0,364):
а)
466 Н;
б)
1280 Н;
в)
1758 Н;
г)
3516 Н. |
23. Визначити нормальну силу в зачепленні зубців шестірні Fn, якщо: діаметр ділильного кола 0,06 м; потужність на валу зубчастої передачі 7 кВт при швидкості 65 с-1 (sin20º=0,342; cos20º=0,94; tg20º=0,364): а) 1795 Н; б) 3589 Н; в) 3820 Н; г) 1250 Н. |
24. Визначити радіальну силу, яка діє на ведене колесо, якщо: потужність на ведучому валу прямозубої передачі 5 кВт при швидкості 100 с-1; діаметр ділильного кола ведучого колеса 0,08 м, передавальне відношення передачі 4 (sin20º=0,342; cos20º=0,94; tg20º=0,364): а) 227,5 Н; б) 455 Н; в) 670 Н; г) 1250 Н. |
25. Розрахувати зусилля в зачепленні коліс, якщо: обертовий момент на ведучому валу циліндричної прямозубої передачі 86 Нм, діаметр ділильного кола 0,05 м:
а)
3440 Н; 1252 Н;
б)
3440 Н; 626 Н;
в)
3440 Н; 606 Н;
г)
3440 Н; 1332 Н. |
Перейдемо до розгляду розділу 4.
Розділ 4
ЗУБЧАСТІ ПЕРЕДАЧІ.
КОСОЗУБІ ТА ШЕВРОННІ КОЛЕСА
Знати будову, принцип роботи, класифікацію і порівняльну характеристику зубчастих передач; особливості геометрії та розрахунку на міцність косозубих і шевронних зубчастих коліс.
У косозубих колесах зубці утворюють із твірною ділильного циліндра кут β. Осі коліс залишаються паралельними. Зубці нарізають тими ж інструментами, що і прямі зубці. У парі зубчастих коліс із зовнішнім зачепленням однакові кути нахилу зубця, але зубці протилежно направлені. У косозубого колеса параметри вимірюють в торцевому (коловому) і нормальному (n–n) напрямах (рис. 4.1).
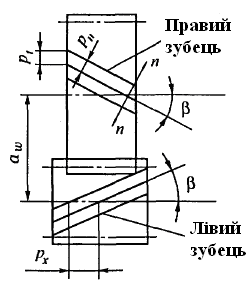
Рис. 4.1. Схема косозубих циліндричних коліс
Нормальний
модуль:
![]() .
.
Крок в нормальному перерізі рn; коловий крок pt.
Коловий
модуль
![]() .
.
Ділильний
діаметр
![]() .
.
Діаметр
вершин
![]() ;
діаметр западин
;
діаметр западин
![]() .
Коефіцієнт осьового перекриття
косозубої передачі
.
Коефіцієнт осьового перекриття
косозубої передачі
![]() ,
де b
– ширина вінця зубчастого колеса; px
– осьовий крок.
,
де b
– ширина вінця зубчастого колеса; px
– осьовий крок.
Сили в зачепленні косозубої передачі
Нормальну силу Fn в зачепленні можна розкласти на три складові (рис. 4.2, а):
![]() ,
,
де
![]() – колова сила,
– колова сила,
![]() ;
;
![]() – радіальна сила
– радіальна сила
![]() ;
;
![]() – осьова сила,
– осьова сила,
![]()
![]() .
.
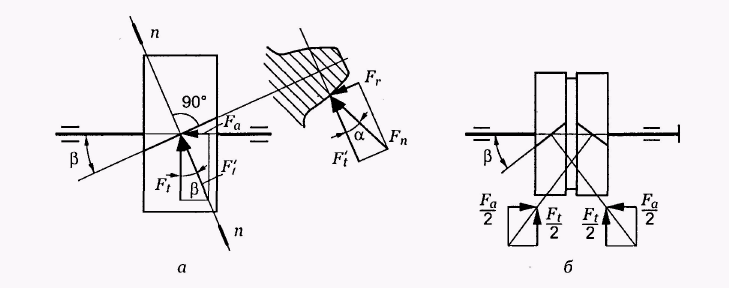
Рис. 4.2. Сили в зачепленні косозубих (а) і шевронних (б) коліс
Під час роботи косозубих передач зубці входять в зачеплення не відразу по всій довжині, а поступово. Навантаження, яке при цьому передається розподіляється на декілька зубців. У зачепленні завжди знаходяться мінімум дві пари зубців. Порівняно з прямозубими передачами підвищуються навантажувальна здатність, плавність і безшумність роботи. Косозубі передачі широко застосовують у техніці.
Із збільшенням кута нахилу збільшуються довжина контактної лінії і коефіцієнт перекриття, тобто плавність і безшумність роботи підвищуються. Одночасно збільшується осьове зусилля, яке додатково навантажує вали і підшипники.
Для обмеження осьових сил кут нахилу вибирають в діапазоні 8...20°, стандартні косозубі колеса виготовляють з кутом β < 15°.
Для зрівноваження осьових зусиль застосовують циліндричні колеса з вінцями, розділеними на ділянки з правим і лівим зубцем, – шевронні колеса. У шевронному колесі осьові сили на напівшевронах напрямлені в різні сторони (рис. 4.2, б): вони зрівноважуються всередині колеса і не передаються на вали і опори. Кути нахилу на шевронних колесах збільшують до 35°, іноді більше. Недоліком шевронних коліс є їх висока вартість.
Розрахунок косозубих коліс на контактну міцність і згин
Проектний розрахунок за контактними напруженнями.
Профіль
косого зубця в нормальному перерізі
співпадає з профілем прямого зубця
mn
=
m.
У колесах з косим зубцем стандартизований
нормальний модуль. При отриманні
формул для розрахунку на міцність
косозубого колеса використовують
еквівалентне
прямозубе колесо,
в якому форма зубця співпадає з формою
зубця в нормальному перерізі косозубого
колеса, радіус якого дорівнює радіусу
кривини еліпса, отриманого в
перерізі n–n
зубця косозубого колеса. Еквівалентне
колесо зображено на рис. 4.3.
Параметри
еквівалентного колеса визначають за
формулами: ділильний діаметр:
![]() ,
,
де
![]() ,
отже,
,
отже,
![]() ;
число зубців:
;
число зубців:
![]() .
.
Ширина еквівалентного прямозубого колеса дорівнює довжині зубця косозубого колеса.
Для розрахунку на міцність за контактними напруженнями і на згин використовуємо формули для прямозубого колеса.
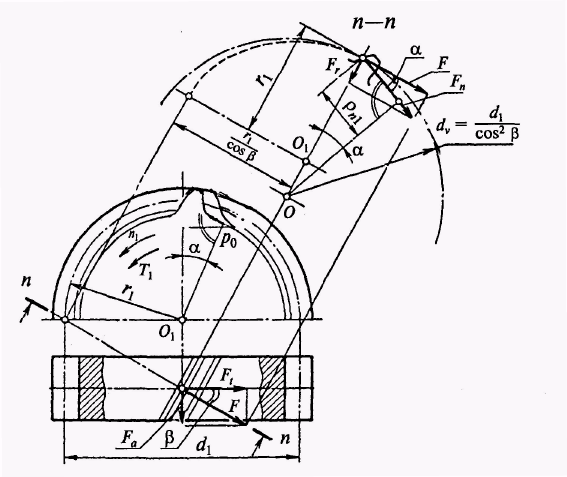
Рис. 5.3. Параметри косозубого (еквівалентного) колеса
Підставивши параметри еквівалентного колеса, отримаємо формулу для проектного розрахунку передачі:
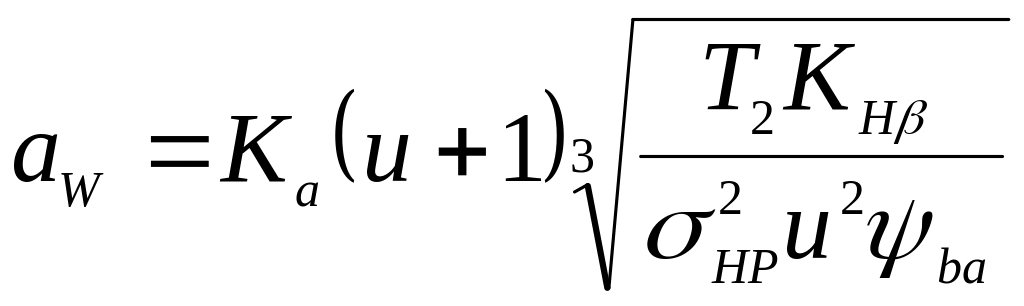 .
.
Для косозубих передач Ka = 430 МПа1/3. Косозубі передачі працюють плавніше, тому коефіцієнт КHβ менший, ніж в прямозубих.
Допустиме напруження розраховують так само, як для прямозубих коліс.
Отримане значення міжосьової відстані округлюють до найближчого стандартного значення, визначають геометричні параметри коліс і перевіряють отриману передачу за контактними напруженнями.
Деякі рекомендації щодо параметрів редукторів наведені в табл. Д8.
Перевірний розрахунок за контактними напруженнями виконують за формулою:
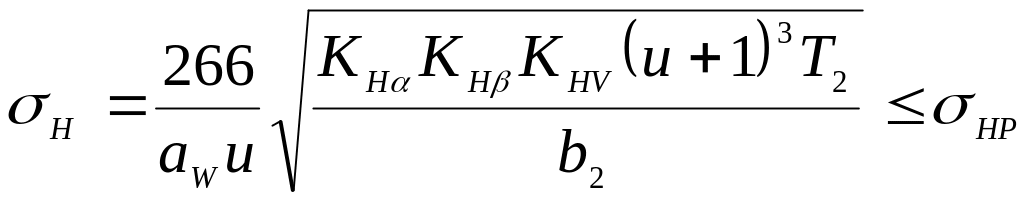 ,
,
де KHα, KHβ, KHV, KFα, KFβ, KFV – коефіцієнти навантаження (див. розрахунок прямозубих передач).
Якщо умова не виконується, збільшують ширину колеса b2; якщо цього недостатньо, збільшують міжосьову відстань.
Перевірка на згин
Похиле положення зубців збільшує їх міцність на згин та плавність роботи. Для розрахунку косозубих коліс використовують формулу для прямозубих і вводять поправочний коефіцієнт Yβ – коефіцфент, що враховує нахил зубця, Yβ = 0,7...0,9.
Перевірку на згин косозубих коліс виконують за формулою:
![]() .
.
Коефіцієнт
форми зубця YF
визначають за таблицями прямозубих
коліс за числом зубців еквівалентного
колеса
![]() .
.
Допустиме напруження визначається так само, як для прямозубих коліс.
Для забезпечення рівної міцності за контактними напруженнями і на згин можна визначити нормальний модуль передачі за формулою:
![]() ,
,
де aW
– отримане
при розрахунку за контактними напруженнями
міжосьова відстань;
![]() .
Перейдемо до розгляду тестових питань
із цієї теми.
.
Перейдемо до розгляду тестових питань
із цієї теми.
Тема: Зубчасті передачі. Косозубі та шевронні колеса
1. Які параметри косозубої циліндричної передачі є стандартизовані: а) m1, aw, z1; б) mn, aw, u; в) mt, z1, u; г) mn, aw, z1. |
2. Вказати основну перевагу косозубих циліндричних передач, порівняно з прямозубими: а) менше зусилля на опорах; б) відсутність періоду однопарного зачеплення; в) низька вартість і доступність матеріалів; г) простота зубонарізання. |
3. Вказати формулу для розрахунку числа зубців еквівалентного прямозубого колеса, що використовується при розрахунках циліндричних косозубих коліс:
а)
в)
|
4. Від чого залежить величина коефіцієнта YF в залежності для перевірки циліндричної косозубої передачі на згин:
а) від z і V; б) від z і m; в) від b і z; г) від z і β. |
5. Яка основна причина обмеження величини кута нахилу зубця в циліндричній косозубій передачі: а) збільшення коефіцієнта перекриття; б) збільшення концентрації напружень в зачепленні; в) збільшення осьового навантаження на підшипники; г) збільшення габаритних розмірів. |
6. Вказати залежність для розрахунку діаметра ділильного кола еквівалентного прямозубого колеса, який використовується для розрахунку циліндричних косозубих коліс:
а)
;
б)
в)
|
7. Вказати формулу для проектного розрахунку косозубих циліндричних коліс: а) в)
|
||||||||||||||||
8. Вказати основний недолік циліндричних косозубих передач: а) збільшення габаритних розмірів; б) збільшення осьового навантаження на опори; в) підвищене зношування робочої поверхні зубця; г) збільшення коефіцієнта перекриття. |
||||||||||||||||
9. Вказати формулу для розрахунку ширини еквівалентного прямозубого колеса, що використовується при розрахунку циліндричних зубчастих коліс: а)
|
||||||||||||||||
10. Що враховує коефіцієнт КНβ в формулі для проектного розрахунку косозубої циліндричної передачі:
а) збільшення міцності за контактними напруженням; б) збільшення коефіцієнта перекриття; в) нерівномірність розподілу навантаження по довжині зубця; г) динамічні (ударні) навантаження в зачепленні. |
||||||||||||||||
11. Вказати формулу для розрахунку радіальної сили в зачепленні зубців циліндричного косозубого колеса: а)
|
||||||||||||||||
12. Вказати основну перевагу шевронної передачі:
а) збільшення сумарної довжини контактних ліній; б) збільшення коефіцієнта перекриття; в) необхідність більш високої точності виготовлення; г) відсутність осьового навантаження опор. |
||||||||||||||||
13. З якою метою при розрахунках косозубого циліндричного колеса використовують поняття «еквівалентне прямозубе колесо»? а) для досягнення рівної міцності за контактними напруженнями і напруженнями згину; б) для отримання залежностей розрахунку на міцність косозубих коліс із відомих формул для прямозубих коліс; в) для розрахунку за готовими формулами; г) для визначення форми косого зубця. |
||||||||||||||||
14. Вибрати формулу для розрахунку осьової сили в зачепленні косозубої циліндричної передачі:
а)
в)
|
||||||||||||||||
15. Яка основна причина обмеження використання шевронних передач: а) збільшення кута нахилу зубців; б) низька навантажувальна здатність; в) велика ширина колеса; г) трудомісткість і велика собівартість виготовлення. |
||||||||||||||||
16. Вказати залежність для перевірки циліндричної косозубої передачі за контактними напруженнями. Яке позначення в цій залежності має коефіцієнт, котрий враховує удари пов’язані зі ступеню точності зубців:
а)
|
||||||||||||||||
17. Визначити колову силу в циліндричній косозубій передачі, якщо: нормальний модуль зубця 2,5 мм; число зубців шестірні 20; кут нахилу зубця 11о; обертовий момент на валу шестірні 44,1 Нм (sin 11º=0,191; cos11º=0,982; tg11º=0,194):
а)
17,64 кН; б)
176 Н; в)
900 Н;
г) 1733 Н.
|
||||||||||||||||
18. Визначити діаметр ділильного кола косозубого циліндричного колеса, якщо: mn= 4мм; z = 21; β=11° (sin 11º=0,191; cos11º=0,982; tg11º=0,194): а) 16,03 мм; б) 82,32 мм; в) 85,6 мм; г) 440,2 мм. |
||||||||||||||||
19. Визначити діаметр кола виступів циліндричного косозубого колеса, якщо: число зубців шестірні 19; передавальне відношення передачі 2,53; нормальний модуль зубців 2 мм; кут нахилу зубця 11º (sin 11º=0,191; cos11º=0,982; tg11º=0,194): а) 97,8 мм; б) 38,7 мм; в) 42,7 мм; г) 101,8 мм. |
||||||||||||||||
20. Визначити міжосьову відстань циліндричної косозубої передачі, якщо: нормальний модуль зубців 1,75 мм, число зубців шестірні 22, передавальне відношення 3,15, кут нахилу зубця 12о (sin 12º=0,208; cos12º=0,978; tg12º=0,213): а) 45 мм; б) 63 мм; в) 81 мм; г) 163 мм. |
||||||||||||||||
21. Визначити радіальну силу в зачепленні циліндричної косозубої передачі, якщо: обертовий момент на валу шестірні 20 Нм, діаметр ділильного кола 65 мм, кут нахилу зубця 10о (sin 10º=0,174; cos11º=0,985; tg11º=0,191):
а)
110,1 Н; б)
227,5 Н; в)
615,44 Н; г)
1665 Н. |
||||||||||||||||
22. Розрахувати осьову силу в зачепленні косозубої циліндричної передачі, якщо: торцевий модуль mt=5,11 мм, число зубців шестірні 21, кут нахилу зубця 12о, обертовий момент на валу шестірні 34,5 Н·м:
а)
136,7 Н; б)
643 Н; в)
1024 Н; г)
3024,5 Н.
|
||||||||||||||||
23. Визначити діаметр кола западин косозубого циліндричного колеса, якщо: число зубців колеса 18, торцевий модуль 3,55 мм, кут нахилу зубця 10о (sin10º=0,1736; cos10º=0,9848; tg10º=0,1763): а) 55,2 мм; б) 63 мм; в) 71 мм; г) 77,5 мм. |
||||||||||||||||
24. По якому з
коліс пари необхідно виконати розрахунок
на згин, якщо допустимі напруження
згину для пари коліс косозубої
циліндричної передачі
а) по колесу 1; б) по колесу 2; в) по будь-якому із коліс; г) розрахунок на згин не виконується. |
||||||||||||||||
25. Розрахувати коефіцієнт форми зубця для косозубої циліндричної передачі на згин, якщо: діаметр ділильного кола колеса 54,6 мм: число зубців 21, кут нахилу зубця 10о (sin 10º=0,1736; cos10º=0,9848; tg10º=0,1763): а) 3,66; б) 3,80; в) 3,98; г) 4,09. |
Перейдемо до розгляду останнього розділу першої частини: до теми «Конічні зубчасті передачі».
Розділ 5
КОНІЧНІ ЗУБЧАСТІ ПЕРЕДАЧІ
Знати основні характеристики, геометричні і силові співвідношення в прямозубих конічних передачах; зусилля в зачепленні прямозубих конічних коліс; основи розрахунку на контактну міцність і згин.
Конічні зубчасті передачі передають обертовий момент між валами з осями, які перетинаються. Основне застосування знайшли передачі з осями валів, які перетинаються під кутом 90°. Передачі з міжосьовим кутом, відмінним від 90°, застосовують рідко через складність виготовлення.
Зачеплення
конічних коліс можна розглядати як
кочення ділильних колових конусів
шестірні і колеса. Діаметри основи
ділильних конусів шестірні і колеса
і їх числа зубців
зв’язані
співвідношенням
![]() (рис.
5.1).
При
куті Σ
=
90°
(рис.
5.1).
При
куті Σ
=
90°
![]() ,
,
![]() .
.
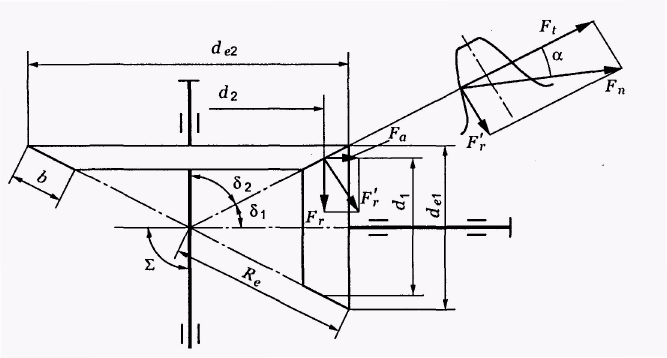
Рис. 5.1. Сили в зачепленні конічної передачі
Основні параметри конічного зубчастого колеса
Довжину відрізка ділильного конуса від вершини до основи називають зовнішньою конусною відстанню Re.
Ширина зубчастого вінця b визначається відстанню між зовнішнім і внутрішнім торцями по твірній ділильного конуса
![]() .
.
Розміри конічних зубчастих коліс визначають по зовнішньому торцевому перерізу з діаметрами de1 і de2.
Основний
геометричний параметр конічного колеса
– зовнішній
коловий
модуль
![]() .
.
![]() (див. рис. 5.1,
5.2)
(див. рис. 5.1,
5.2)
Розрахунки
конічних коліс на міцність проводять
по середньому
ділильному діаметру
![]() .
.
Середній
модуль зубця
![]() .
.
Середні
ділильні діаметри
![]() .
.
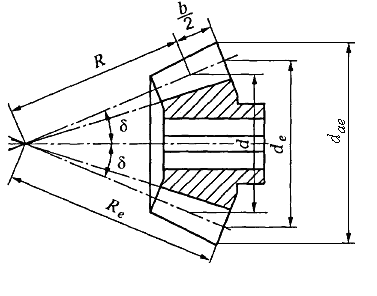
Рис. 5.2. Геометричні параметри конічного колеса
Зубці конічних коліс в залежності від зміни перерізу по довжині поділяються на три форми (рис. 5.3). Форма I застосовується в основному для коліс з прямими зубцями. Форма II забезпечує оптимальну міцність на згин, технологічна, використовується для коліс з коловими зубцями. Форма III застосовується для плоских коліс в спеціальних випадках.

Рис. 5.3. Осьова форма зубця конічного зубчастого колеса
Конічні колеса випускають з прямими, косими та круговими зубцями (рис. 5.4). Конічні колеса з круговими зубцями, порівняно з прямозубими, мають більшу несучу здатність, працюють з меншим шумом.
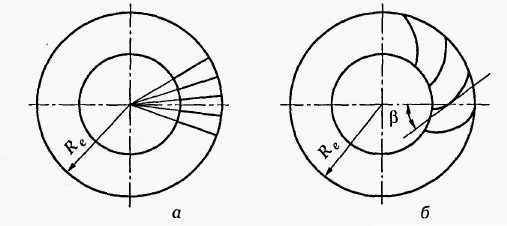
Рис. 5.4. Конічні колеса з прямими (а) і круговими (б) зубцями
Зубці нарізають різцевими головками методом обкатування. Кут нахилу зубця в середньому перерізі 35°, спряжені колеса мають протилежний напрям лінії зубців. Шестірні виконують з правим зубцем, колеса – з лівим.
Загальна характеристика конічних передач
Конічні передачі складніше циліндричних, вимагають періодичного регулювання. Для нарізання зубчастих конічних коліс необхідно мати спеціальний інструмент. Шестірня закріплюється консольно, при цьому збільшується нерівномірність розподілу навантаження. У зачепленні діють осьові сили. Усе це знижує навантажувальну здатність в порівнянні з циліндричними передачами. Однак конічні колеса широко застосовують у техніці, де за умовами компоновки необхідно розташовувати вали під кутом один до одного.
Сили в зачепленні прямозубої конічної передачі
Нормальну силу в зачепленні конічної передачі розкладають на колову і перпендикулярну до неї:
![]() .
.
У свою
чергу, силу
![]() розкладають на осьову і радіальну сили
(див. рис. 6.1):
розкладають на осьову і радіальну сили
(див. рис. 6.1):
![]() .
У
результаті
.
У
результаті![]() ,
,
де
![]() .
.
Для колеса напрям сил, що діють, протилежний. У прямозубій передачі осьова сила завжди направлена до більшого торця, радіальна – до центра колеса.
Основи розрахунку на контактну міцність і згин конічної передачі
Проектний розрахунок за контактними напруженнями
У конічних колесах навантаження по довжині зубця розподілене нерівномірно. Для простоти розрахунок конічних коліс на згин ведуть по середньому перерізу зубця. Розрахунок оснований на припущенні, що навантажувальна здатність конічної передачі рівна навантажувальній здатності еквівалентної циліндричної передачі при ширині колеса, рівній ширині конічних коліс. Модуль циліндричного колеса рівний торцевому модулю конічного колеса.
Діаметр
еквівалентного колеса
![]() .
.
Число
зубців
![]() .
.
При проектному розрахунку визначають зовнішній ділильний діаметр колеса.
Вважають, що навантажувальна здатність конічного колеса складає 0,85 навантажувальної здатності циліндричного:
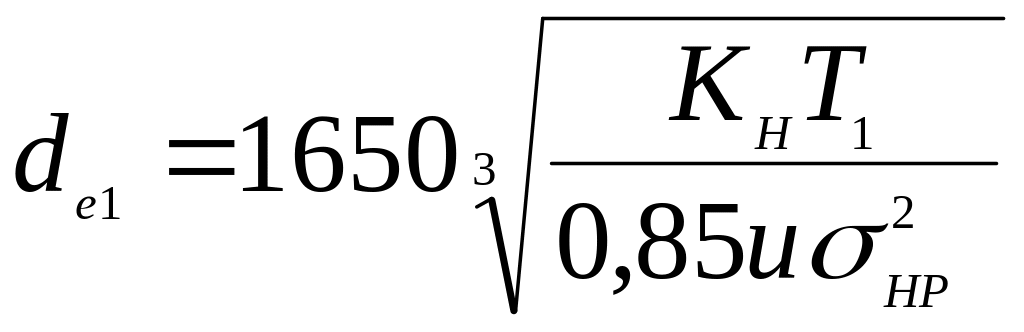 ,
,
де KH – коефіцієнт навантаження.
Допустиме напруження визначають за формулами для циліндричних коліс.
Перевірка на згин
Для
відкритих передач і передач із високою
твердістю поверхні
![]() геометричні параметри коліс визначають
з розрахунку на згин, при цьому
розраховують середній модуль. Для
закритих передач розрахунок на згин є
перевірним. Для перевірного розрахунку:
геометричні параметри коліс визначають
з розрахунку на згин, при цьому
розраховують середній модуль. Для
закритих передач розрахунок на згин є
перевірним. Для перевірного розрахунку:
![]() ,
,
де KF – коефіцієнт навантаження; YF – коефіцієнт форми зубця, вибирається за числом зубців zV; Ft – колова сила; b – ширина зубчастого вінця; m – модуль зубця в середньому перерізі.
Допустиме напруження розраховується так само, як для циліндричних коліс.
Оскільки розрахунок конічних передач на міцність подібний до розрахунку циліндричних передач, тому тестові питання з цієї теми знаходяться в попередніх розділах і повністю охоплюють геометричний розрахунок і розрахунок на міцність цієї передачі.
Перейдемо до розгляду наступного розділу: «Передача гвинт–гайка».
Розділ 6
ПЕРЕДАЧА ГВИНТ–ГАЙКА
Мати уяву про призначення передачі, матеріали деталей передачі, чинники, що впливають на ККД.
Знати види руйнувань і критерії працездатності; формули для кінематичного і геометричного розрахунків.
Передача «гвинт–гайка» використовується для перетворення обертового руху однієї з ланок в поступальний рух іншої (рис. 6.1).
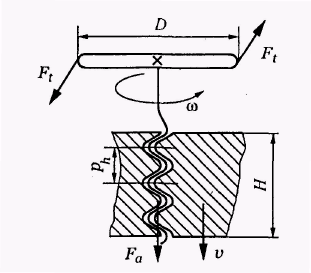
Рис. 6.1. Схема передачі «гвинт–гайка»
Гвинти в передачі поділяються на вантажні та ходові.
Вантажні гвинти використовують в домкратах, гвинтових пресах і натискних пристроях.
Ходові гвинти застосовують у верстатах і вимірювальних приладах для установочних, робочих і неробочих переміщень.
Основна вимога до передачі – зносостійкість і тривале збереження точності.
У залежності від виду тертя в різьбі передачі діляться на передачі ковзання і передачі кочення (рис. 6.2).
У домкратах і гвинтових пресах застосовують упорну різьбу, у гвинтових передачах зазвичай використовують трапецеїдальну різьбу.
Передавальне відношення передачі «гвинт–гайка»:
![]() ,
,
де D – діаметр маховичка; ph – хід гвинта (див. рис. 6.1): ph = pz,
де p – крок різьби; z – число заходів різьби.
Ведучою ланкою може бути як гвинт, так і гайка.
Швидкість поступального руху, мм/с, в залежності від кутової швидкості ω, с-1, гвинта:
![]() .
.
Оцінка передачі «гвинт–гайка»
Переваги передачі «гвинт–гайка»:
простота конструкції;
малі габаритні розміри при великій несучій здатності;
велике передавальне число;
можливість виготовлення з великою точністю;
самогальмування в передачі.
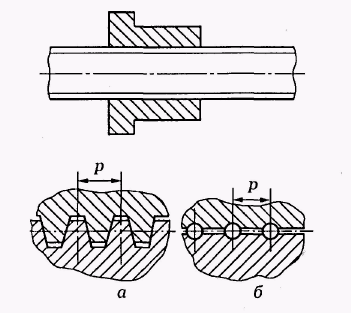
Рис. 6.2. Передача «гвинт–гайка»: а – ковзання; б – кочення
Основний недолік передачі «гвинт–гайка» – низький ККД. При використанні передачі кочення ККД збільшується, але такі передачі складні і їх вартість вища.
Матеріали
Гвинти виготовляють зі сталі 45 або 50, а гайки з олов’яних бронз БрО10Ф0,5 та Бр6Ц6С3.
Важконавантажені передачі кочення виготовляють з хромистих сталей, загартованих до твердості 61 HRC (ХВГ, 8 ХВ та ін.).
Силове співвідношення в передачі «гвинт–гайка»
Колова сила на маховичку (див. рис. 6.1)
![]() ,
,
де Fa – осьова сила на гайці (гвинті); і – передавальне відношення передачі; η – ККД передачі:
![]() ,
,
де ψ
– кут підйому гвинтової лінії (рис.
6.3);
![]() – коефіцієнт тертя;
– коефіцієнт тертя;
![]() .
.
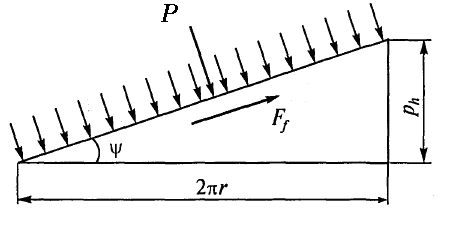
Рис. 6.3. Розвертка витка; Р – питомі навантаження між витками;
Ff – сила тертя в різьбі
Критерії працездатності і розрахунок передачі «гвинт – гайка»
Основним критерієм працездатності є зносостійкість різьби. Для зменшення зношування застосовують антифрикційні пари матеріалів (сталь – бронза, сталь – чавун), змащування поверхонь, малі допустимі напуження зминання.
Різьбу перевіряють на зминання. Розраховують питомі навантаження на поверхні витків з умови невитискування мастильного матеріалу. Міцність тіла гайки розраховують з умови міцності на розтяг. Гвинти перевіряють на стиск і стійкість.
Розрахунок
на зносостійкість різьби проводять за
допустимим питомим навантаженням
![]() з подальшою перевіркою болта на міцність:
з подальшою перевіркою болта на міцність:
![]() ,
,
де d2 – середній діаметр різьби; H1 – робоча висота профілю різьби; ZВ – число витків гайки.
Для проектного розрахунку передачі:
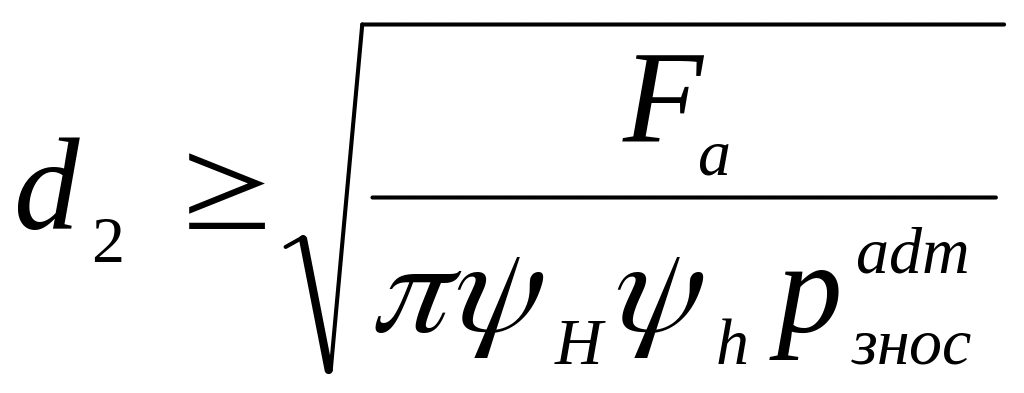 ,
,
де
![]() ,
,
![]() 1,2...2,5
– коефіцієнт висоти гайки; ψh
– коефіцієнт робочої висоти
профілю різьби; ψH
= 0,5 (трапецеїдальна різьба); ψh
= 0,75 (упорна різьба).
1,2...2,5
– коефіцієнт висоти гайки; ψh
– коефіцієнт робочої висоти
профілю різьби; ψH
= 0,5 (трапецеїдальна різьба); ψh
= 0,75 (упорна різьба).
Зовнішній діаметр гайки:
![]() ,
,
де d – зовнішній діаметр різьби.
Тестові питання з цієї теми закладені в основу розділу «Черв’ячні передачі», тому розгдядати їх окремо немає змісту.
Розділ 7
ЧЕРВ’ЯЧНІ ПЕРЕДАЧІ
Знати принцип роботи, особливості робочого процесу; причини виходу з ладу і критерії працездатності черв’ячних передач; геометричні і силові співвідношення в черв’ячних передачах; формули для розрахунку на міцність.
Черв’ячна передача – передача зачепленням з перехресними осями валів. Передача руху відбувається від черв’яка (однозахідного або багатозахідного гвинта) до зубчастого колеса спеціальної форми і здійснюється за принципом гвинтової пари (рис. 8.1).
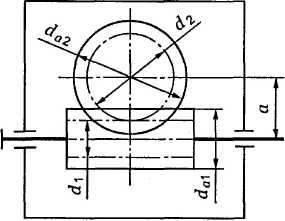
Рис. 7.1. Схема черв’ячної передачі
У передачі виникає значне взаємне ковзання витків черв’яка по зубцях колеса, що викликає підвищене зношування і значне виділення теплоти. Для зменшення тертя вінці черв’ячних коліс виготовляють з антифрикційних матеріалів (бронзи, рідше чавуна).
Проводиться тепловий розрахунок і визначаються способи охолоджування.
Зачеплення вимагає періодичних регулювань.
Оцінка черв’ячних передач
До переваг черв’ячних передач необхідно віднести велике передавальне число, компактність, невелику масу, плавність і безшумність роботи, можливість отримання самогальмування.
Самогальмування – можливість передачі руху лише від черв’яка до колеса; можна використовувати механізм без гальмівних пристроїв, що перешкоджають зворотньому руху колеса.
Основні параметри черв’ячної передачі
Розглядається передача без зміщення (рис. 7.2).
Основним розрахунковим параметром черв’яка є осьовий модуль:
![]() .
.
Ділильний
діаметр черв’яка
![]() ,
де q
– коефіцієнт діаметра черв’яка.
Значення m
і q
стандартизовані (див. табл. Д9).
,
де q
– коефіцієнт діаметра черв’яка.
Значення m
і q
стандартизовані (див. табл. Д9).
Число заходів черв’яка z1 = 1; 2; 4.
Ділильний
кут підйому витка черв’яка γ,
![]() (рис.
7.3).
(рис.
7.3).
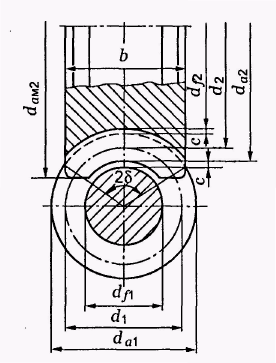
Рис. 7.2. Геометричні параметри черв’ячної передачі
Осьовий модуль черв’яка дорівнює торцевому модулю черв’ячного колеса.
Діаметр
ділильного кола колеса
![]() .
.
Діаметр
вершин зубців в середньому перерізі
![]() .
.
Діаметр
западин черв’ячних коліс в середньому
перерізі
![]() .
.
Найбільший
діаметр черв’ячного колеса
![]() .
.
Зубці коліс мають вгнуту форму і охоплюють черв’як по дузі з кутом 2δ.
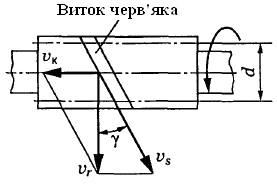
Рис. 7.3. Ковзання в передачі: VK – лінійна швидкість зубця колеса; Vr – лінійна швидкість витка черв’яка; VS – швидкість взаємного ковзання
Ширина вінця b.
Міжосьова
відстань передачі
![]() .
.
Число зубців черв’ячного колеса z2.
Передавальне
число черв’ячної передачі
![]() ;
z2=30÷80;
z1=1;
2; 4. Тоді – u
= 8÷80.
;
z2=30÷80;
z1=1;
2; 4. Тоді – u
= 8÷80.
ККД черв’ячної передачі
ККД черв’ячної передачі враховує втрати в зубчасто-гвинтовій парі, в підшипниках і втрати на розмішування та розбризкування мастила.
ККД черв’ячної передачі можна визначити за формулою:
![]() ,
,
де
![]() – зведений кут тертя;
– зведений кут тертя;
![]() – кут підйому лінії витка.
– кут підйому лінії витка.
ККД черв’ячної передачі в залежності від числа заходів черв’яка:
z1 = 1; η = 0,7...0,75; z1= 2; η = 0,75...0,87; z1= 4; η = 0,87...0,92.
Сили в зачепленні черв’ячної передачі
Силу взаємодії витка черв’яка із зубцем колеса розкладають на три складові (рис. 7.4): Ft, Fr, Fa.
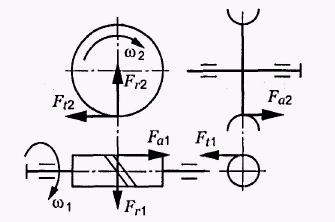
Рис. 7.4. Сили в черв’ячній передачі
Колова сила на черв’яку дорівнює осьовій силі на колесі:
![]() .
.
Осьова сила на черв’яку дорівнює коловій силі на колесі:
![]() .
.
Радіальні сили рівні між собою:
![]() .
.
Обертовий момент на колесі:
![]() .
.
Види руйнувань зубців коліс черв’ячних передач
У черв’ячній парі слабкою ланкою є зубець черв’ячного колеса. Відбуваються поверхневі пошкодження: втомне викришування, зношування поверхні, заїдання. Вкрай рідко виникає злам зубця. Зубчасті вінці найчастіше виготовляють з бронзи. Вибір марки залежить від швидкості ковзання в передачі (див. рис. 7.3, табл. Д10).
У передачах з вінцями коліс з олов’яних бронз найбільш небезпечне покриття робочих поверхонь, в колесах з безолов’яних (алюмінієво-залізних) бронз і чавунів частіше відбувається заїдання, яке потім переходить в задири зі зношуванням поверхні.
Розрахунок на міцність черв’ячної передачі
Розрахунок за контактними напруженнями є основним (проектним), а за напруженнями згину – перевірним.
В основу розрахунку за контактними напруженнями закладена формула Герца. Після підстановки параметрів черв’ячного колеса, коефіцієнтів, що враховують характер навантаження, і відповідних перетворень отримана формула для перевірного розрахунку передачі:
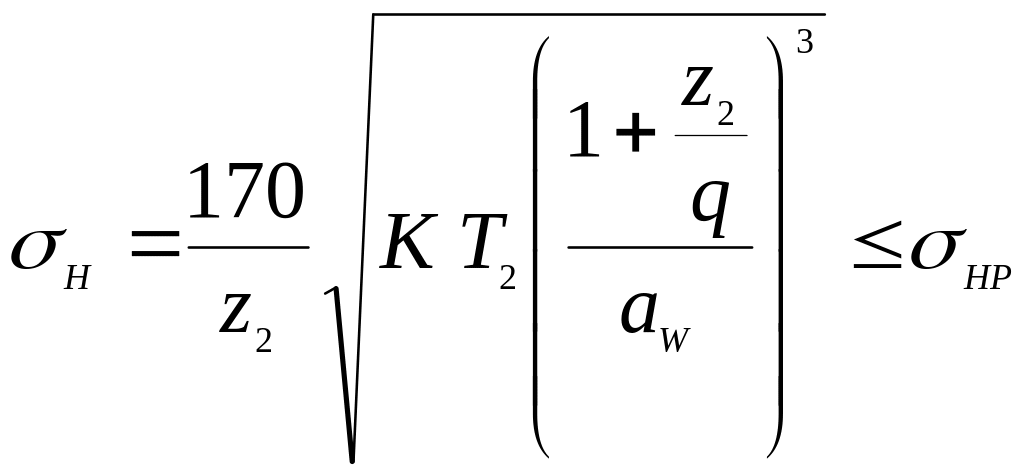 .
.
Визначивши із отриманої формули міжосьову відстань, отримаємо формулу для проектного розрахунку черв’ячної передачі:
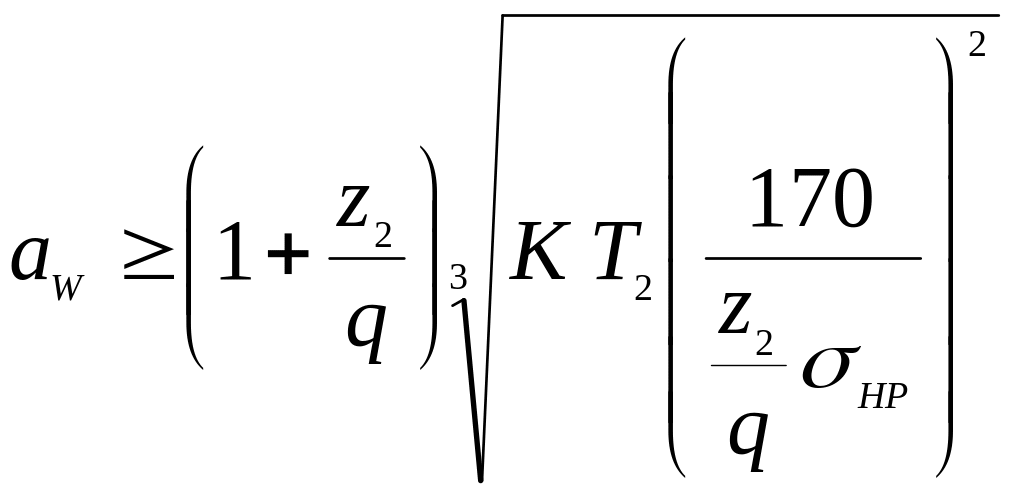 .
.
При
розрахунку задаються орієнтовними
значеннями ККД редуктора,
швидкості ковзання в передачі, визначають
обертові моменти. За прийнятою
величиною швидкості ковзання вибирають
матеріал вінця колеса і визначають
допустимі напруження. За заданим
передавальним числом
визначають число заходів черв’яка і
число зубців колеса:
![]() .
.
Отримане при розрахунку aw округлюють до стандартного значення (див. табл. Д3).
За стандартною міжосьовою відстанню визначають геометричні параметри передачі.
Визначають зусилля в зачепленні. Проводять перевірку отриманої передачі на згин.
Формула для перевірного розрахунку передачі на згин:
![]() ,
,
де KF
– коефіцієнт навантаження; YF
– коефіцієнт форми зубця, вибирається
за зведеним числом зубців
![]() (табл. Д6).
(табл. Д6).
Швидкість ковзання в передачі (див. рис. 7.3):
![]() .
.
Рекомендації щодо розрахунку на міцність черв’ячної передачі
1. Після розрахунку міжосьової відстані модуль передачі визначають за формулою:
![]() .
.
2. Мінімальне
значення q
за умови жорсткості черв’яка
![]() .
Отримане значення уточнюють зі стандартом
(табл. Д9),
при цьому можна змінити z2,
збільшуючи або зменшуючи на 1–2 зубці.
.
Отримане значення уточнюють зі стандартом
(табл. Д9),
при цьому можна змінити z2,
збільшуючи або зменшуючи на 1–2 зубці.
3. Ширина вінця черв’ячного колеса залежить від числа витків черв’яка: при z1 = 1; 2 b2 = 0,355аW;
при z2 = 4 b2 = 0,315аW.
4. Допустимі напруження для матеріалів вінця колеса залежать від способу відливання і марки бронзи або чавуну, від твердості робочої поверхні черв’яка, довговічності передачі.
Тепловий розрахунок черв’ячної передачі
Унаслідок невисокого ККД в черв’ячних передачах генерується велика кількість теплоти. Мастило, деталі передачі і стінки корпусу нагріваються.
Якщо відведення теплоти недостатнє, передача перегрівається, різко зменшується в’язкість мастила, виникає небезпека витискування мастильного матеріалу і заїдання.
Тепловий розрахунок передачі проводять з умови теплового балансу: тепловиділення повинне дорівнювати тепловіддачі за одиницю часу.
Кількість теплоти, яка виділяється в передачі в секунду
![]() ,
,
де
![]() – потужність, що підводиться до передачі,
Вт;
– потужність, що підводиться до передачі,
Вт;
![]() – ККД черв’ячної передачі.
– ККД черв’ячної передачі.
Кількість теплоти, яка віддається через стінки корпуса редуктора навколишньому середовищу
![]() ,
,
де
![]() – коефіцієнт теплопередачі,
=
(9…17)
– коефіцієнт теплопередачі,
=
(9…17)![]() ;
;
![]() – площа охолоджуваної поверхні,
– площа охолоджуваної поверхні,
![]() ;
;
![]() – температура середовища, в якому
працює передача, ºС;
– температура середовища, в якому
працює передача, ºС;
![]() – температура мастила, ºС.
– температура мастила, ºС.
Рівняння теплового балансу виглядає наступним чином:
![]() ,
тобто
,
тобто
![]() ,
,
Температура мастила визначається за формулою
![]() .
.
Отримане значення слід порівняти із допустимим, тобто повинна виконуватись умова
![]() ,
,
де
![]() –
допустима температура мастила, що
становить 75…85ºС.
–
допустима температура мастила, що
становить 75…85ºС.
Тема: Черв’ячні передачі
1. Яким повинно бути число заходів черв’яка та число зубців колеса, щоб отримати передавальне відношення черв’ячної передачі 18: а) 1; 18 б) 3; 78 в) 2; 64 г) 2; 36. |
2. Вибрати формулу для перевірного розрахунку черв’ячної передачі за контактними напруженнями:
а)
в)
|
3. Яким повинно бути число заходів черв’яка та число зубців колеса, щоб отримати передавальне відношення передачі 26: а) 1; 30 б) 2; 52 в) 3; 78 г) 4; 104. |
4. Вказати основні недоліки черв’ячних передач: а) зношування і нагрівання деталей передачі; б) самогальмування; в) обмеження по обертовому моменту; г) значні розміри передачі. |
5. Що враховує при розрахунку черв’ячної передачі за контактними напруженнями коефіцієнт К у формулі:
а) ковзання передачі; б) підвищення температури; в) поштовхи та вібрації при роботі; г) зменшення міцності в порівнянні з циліндричною передачею. |
6. Вибрати формулу для розрахунку діаметра ділильного кола черв’яка: а)
;
б)
|
7. Вибрати орієнтоване значення ККД черв’ячної передачі, якщо число заходів черв’яка 2: а) 0,82…0,87; б) 0,75…0,82; в) 0,87…0,92; г) 0,70…0,75. |
8. Як визначити коефіцієнт YF2 при розрахунку черв’ячної передачі на згин у формулі:
а)
за характером навантаження; б)
за величиною
|
9. Вказати формулу для розрахунку ККД черв’ячної передачі: а)
|
10. Котрий з перерахованих факторів інтенсифікує тертя в черв’ячній передачі: а) застосування спеціальних матеріалів; б) використання спеціальних мастильних матеріалів; в) обробка поверхні; г) зменшення кута нахилу гвинтової лінії черв’яка. |
11. Вибрати формулу для розрахунку міжосьової відстані черв’ячної передачі:
а)
в)
;
г)
|
12. Вибрати формулу для проектного розрахунку черв’ячної передачі: а)
в)
|
13. Розрахувати діаметр вершин витків черв’яка, якщо: m = 3,15 мм; q = 12,5; z1 = 2: а) 45,67 мм; б) 39,38 мм; в) 31,71 мм; г) 29,74 мм. |
14. Визначити швидкість ковзання в черв’ячному зачепленні, якщо: кут підйому витка червяка 14º, модуль зачеплення 4 мм; коефіцієнт діаметра черв’яка 16; кутова швидкість черв’яка 150 с-1:
а)
1,19 м/с; б)
3,86 м/с; в)
4,8 м/с; г)
4,95 м/с.
|
15. Визначити величину осьового зусилля на черв’яку, якщо: обертовий момент на ведучому валу передачі 52 Нм; передавальне відношення 25; ККД передачі 0,75; модуль зачеплення 2,5 мм; число зубців колеса 50:
а)
0,99кН; б)
15,6 кН; в)
37,14 кН; г)
78,12 кН.
|
16. Визначити передавальне відношення черв’ячної передачі, якщо: число заходів черв’яка 2; модуль зачеплення 2 мм; коефіцієнт діаметра черв’яка 8; діаметр ділильного кола колеса 96 мм: а) 6; б) 24; в) 48; г) 12. |
17. Визначити міжосьову відстань, якщо: z1= 2; z2=32; коефіцієнт діаметра черв’яка 16; модуль зачеплення 4 мм. Результат округлити до найближчого стандартного значення:
а)
100 мм; б)
125 мм; в)
140 мм; г)
160 мм.
|
18. Визначити величину осьового зусилля на колесі черв’ячної передачі, якщо: потужність на ведучому валу 4,5 кВт, кутова швидкість вала 100 с-1, модуль зачеплення 2,5 мм, коефіцієнт діаметра черв’яка 10:
а)
4 кН; б)
1,8 кН; в)
3,6 кН; г)
18,57 кН. |
19. Визначити число заходів черв’яка, якщо: відомо що кутова швидкість черв’яка 150 с-1; швидкість колеса 3,65 с-1; число зубців колеса 78: а) 1; б) 2; в) 3; г) 5. |
20. Визначити коефіцієнт діаметра черв’яка, якщо: число заходів черв’яка 4; кут підйому гвинтової лінії черв’яка 14º: а) 8; б) 10; в) 12,5; г) 16. |
21. Визначити величину радіального зусилля на черв’яку, якщо: потужність на ведучому валу передачі 6 кВт; ККД передачі 0,75; кутова швидкість колеса 2 с-1; діаметр ділильного кола колеса 420 мм; кут зачеплення 20º:
а)
14,28 кН; б)
5,20 кН; в)
10,71 кН; г)
3,9 кН.
|
22. Визначити величину радіального зусилля на колесі передачі, якщо: обертовий момент на ведучому валу передачі 62,5 Н·м; передавальне відношення передачі 31; ККД передачі 0,8; модуль зачеплення 4 мм; число зубців 62; кут зачеплення 20º:
а)
4,55 кН; б)
6,25 кН; в)
12,5 кН; г)
15,5 кН.
|
23. Визначити число заходів черв’яка та число зубців колеса, якщо: кутова швидкість на вхідному та вихідному валах передачі 74 і 1,54 с-1 відповідно: а) 1, 48; б) 2, 100; в) 3, 129; г) 4, 172. |
24. Визначити кут підйому гвинтової лінії, якщо: число заходів черв’яка 2; коефіцієнт діаметра черв’яка 16: а) 7°10´; б) 14°; в) 82°55´; г) правильна відповідь не наведена. |
25. Визначити колове зусилля на колесі черв’ячної передачі, якщо: потужність на вхідному валу передачі 2,4 кВт; кутова швидкість передачі вхідного вала 100 с-1; ККД передачі 0,75; передавальне відношення 48; модуль зубців 5 мм; число заходів черв’яка z1= 1: а) 864 Н; б) 7,2 кН; в) 14,4 кН; г) 3,6 кН. |
Розділ 8
ФРИКЦІЙНІ ПЕРЕДАЧІ І ВАРІАТОРИ
Мати уяву про принцип роботи, переваги і недоліки фрикційних передач і варіаторів основних типів.
Знати формули для розрахунку передавального відношення передачі з урахуванням і без урахування ковзання в передачі, для розрахунку сили тертя, момента тертя, зусилля натискання пружини; пристрій, матеріали, причини виходу із ладу і критерії працездатності фрикційних передач; формули для визначення діапазону регулювання варіаторів основних типів; формули для розрахунку на контактну міцність і вміти ними користуватися.
Фрикційна передача – це передача, в якій рух передається силами тертя. Прості фрикційні передачі (рис. 8.1) складаються з двох коліс (котків), які притискаються один до одного з силою, яка створює силу тертя і рівна величині колового зусилля. Сила притискання котків може створюватися власною вагою конструкції, важелями, пружинами або спеціальними пристроями.
Основні характеристики фрикційної передачі
Передавальне число без урахування проковзування:
![]() .
.
Сила тертя в контакті:
![]() ,
,
де f – динамічний коефіцієнт тертя (табл. Д11 ); Q – сила притискання.
Для
випадку, зображеного на рис. 8.1,
![]() .
.
Момент тертя, який створюється при цьому:
![]() .
.
Сила притискання:
![]() ,
,
де K – коефіцієнт запасу зачеплення.
У відповідальних випадках застосовується автоматичне притискання (самозатягування), яке пропорційне переданому моменту.
Рис. 8.1. Схема циліндричної фрикційної передачі
Ковзання у фрикційній передачі
Ковзання у фрикційній передачі пов’язане з пружніми деформаціями поверхневих шарів, зносом поверхонь, можливим послабленням притискання котків, можливою несталістю коефіцієнта тертя.
Ковзання у фрикційній передачі залежить від навантаження. При перевантаженні може настати буксування, при цьому ведучий коток ковзає по веденому, ведений коток зупиняється.
Буксування призводить до інтенсивного руйнування робочих поверхонь.
Передавальне число фрикційної передачі з урахуванням ковзання:
![]() ,
,
де ε – коефіцієнт ковзання:
![]() ,
,
де V1, V2 – лінійні швидкості в точці контакту. Зазвичай ε = 0,002...0,05.
Матеріали
Основні вимоги до матеріалів:
зносостійкість і контактна міцність;
високий коефіцієнт тертя;
високий модуль пружності, щоб не виникала значна деформація площі контакту і не збільшувалися втрати на тертя.
При матеріалах гартована сталь – гартована сталь забезпечуються невеликі габаритні розміри передачі і високий ККД; використовують кулькопідшипникові сталі з гартуванням до 60 HRC.
Поєднання чавун – чавун або чавун – сталь дозволяє працювати з мастилом і без нього (насухо).
Поєднання сталь – текстоліт дозволяє працювати без змащування, динамічний коефіцієнт тертя спеціальних пластмас досягає 0,5.
Застосовують тіла кочення, покриті шкірою або гумою. Ці матеріали забезпечують високий динамічний коефіцієнт тертя, але він залежить від вологості повітря. Такі колеса мають низьку контактну міцність. Інколи використовують покриття із дерева.
Оцінка фрикційних передач
Надійні передачі, в яких ведучий шків виконаний з менш твердого матеріалу.
Переваги фрикційних передач:
простота конструкції;
безшумність і плавність роботи;
можливість безступінчастого регулювання передавального числа. Недоліки фрикційних передач:
значні питомі навантаження на вали й опори, які обмежують величину потужності;
ковзання в передачі, що викликає несталість передавального числа навіть при ретельному виготовленні і монтажі передачі.
Види руйнувань і критерії працездатності передачі:
втомне викришування робочих поверхонь;
заїдання у важконавантажених швидкохідних передачах, які працюють із змащенням;
при розриві мастильної плівки утворюються приварені частинки, які задирають поверхню у напрямі ковзання;
зношування поверхні частіше нерівномірне. Підвищене зношування спостерігається у відкритих передачах.
Для фрикційних передач з металевими котками основним критерієм працездатності є контактна міцність. Міцність і довговічність фрикційних передач оцінюються за контактними напруженнями – напруженнями зминання поверхні на площі контакту.
Розрахунок на міцність фрикційної передачі
Схема для розрахунку циліндричної фрикційної передачі зображена на рис. 8.2.
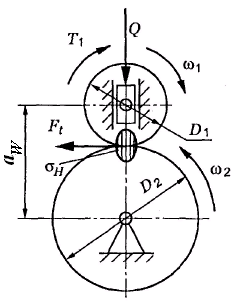
Рис. 8.2. Розрахункова схема циліндричної фрикційної передачі
Контактне напруження передач із контактом по лінії визначаються за формулою Герца:
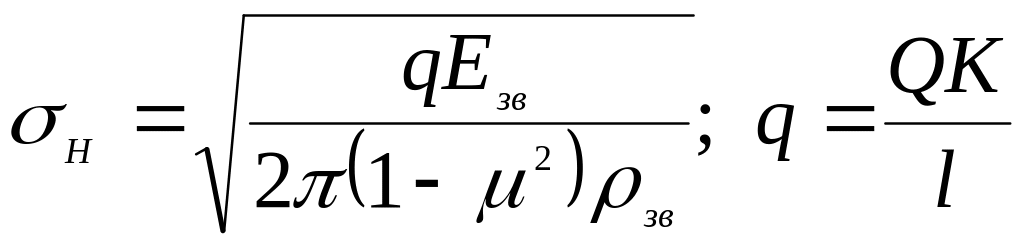 ,
,
де q – нормальне навантаження по довжині контактної лінії; Q – сила притискання котків; K – коефіцієнт запасу зчеплення (коефіцієнт навантаження), K = 1,25…2; l – довжина контактної лінії; ρзв – зведений радіус кривини:
![]() ;
;
Езв
– зведений модуль пружності,
![]() ;
;
μ – коефіцієнт поперечної деформації.
При μ = 0,3 отримаємо умову міцності за контактними напруженнями:
![]() ,
,
де
![]() – допустиме контактне напруження для
менш міцнішого матеріалу котків.
– допустиме контактне напруження для
менш міцнішого матеріалу котків.
Варіатори
Варіатори служать для плавної (безступінчастої) зміни швидкості обертання веденого валу на ходу при сталій швидкості ведучого валу. У залежності від форми тіл кочення варіатори поділяються на лобові, конусні, торові, дискові, клинопасові та інші. Основна характеристика варіатора – діапазон регулювання:
.
Лобові варіатори (рис. 8.3, а) прості, їх виконують реверсними. При зміні положення ролика 1 змінюється радіус веденої ланки. Діапазон регулювання лобового варіатора:
![]() .
.
Конусні варіатори без проміжної ланки (рис. 8.3, б) за діапазоном регулювання аналогічні лобовим і можуть забезпечити зміну напрямку обертання.
Конусні варіатори з паралельними валами і проміжним елементом (рис. 8.3, е) можуть працювати лише в режимі пришвидшення або сповільнення.
Торові варіатори (рис. 8.3, в) складаються з торових чашок і роликів. Зміна швидкості на виході досягається поворотом осей обертання роликів. Зі всіх типів варіаторів торові варіатори найбільш досконалі, їх недолік – складність конструкції. Діапазон регулювання торового варіатора:
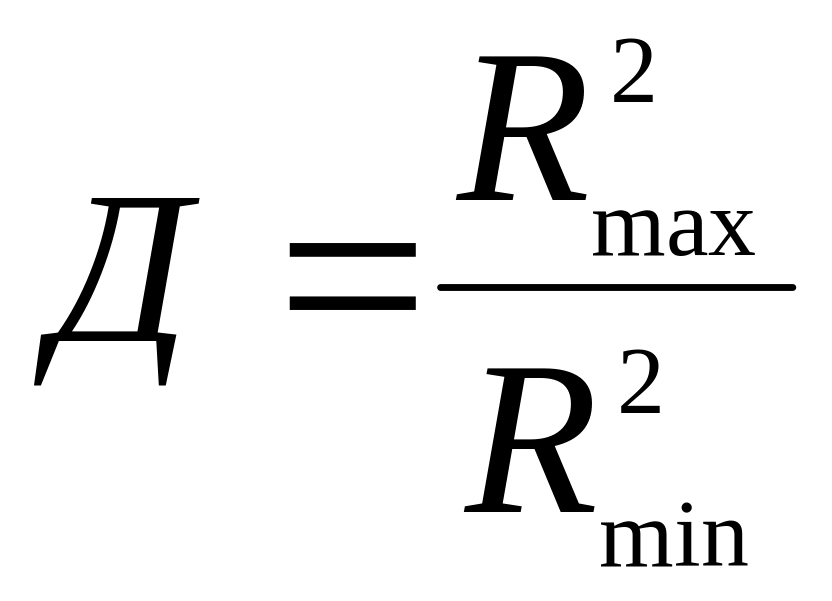 .
.
Багатодискові варіатори (рис. 8.3, г) складаються з пакетів конічних розсувних дисків, що притискаються пружинами. Регулювання швидкості відбувається зміщенням осі ведучого валу, відносно веденого; змінюється величина радіуса контакту.
ККД варіатора 0,75...0,85.
Діапазон регулювання дискового варіатора:
.
Варіатори з розсувними шківами і широкими клиновими пасами (рис. 8.3, д) прості і надійні. Їх випускають у вигляді самостійних агрегатів і вмонтовують у вузли механізмів. Швидкість регулюється зміною розрахункових діаметрів шківів з допомогою осьового переміщення дисків. Діапазон регулювання таких варіаторів:
![]() .
.
Варіатори нестандартизовані, ККД = 0,8...0,9.
Практично для одноступеневих варіаторів діапазон регулювання Д = 3...8.
77
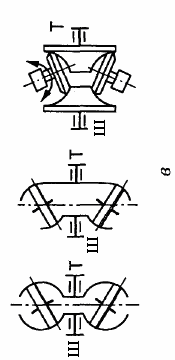
.
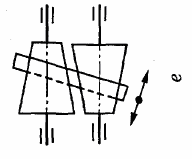
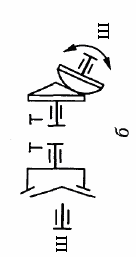
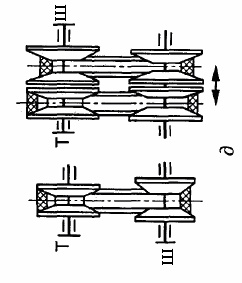
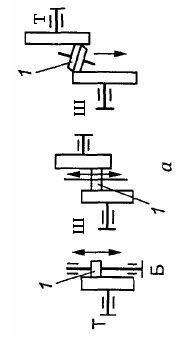
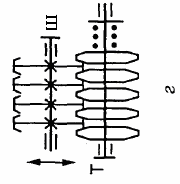
Тема: Фрикційні передачі і варіатори
1. Вказати основні переваги фрикційних передач: а) безшумність та плавність роботи; б) сталість передавального відношення; в) мале навантаження на опори; г) низька вартість та доступність матеріалів. |
2. Вказати формулу для точного розрахунку передавального відношення фрикційної передачі: а)
|
3. Визначити коефіцієнт тертя, який необхідно використовувати при розрахунку зображеної фрикційної передачі:
а) сталь по сталі (насухо), f=0,15; б) текстоліт по сталі, f=0,2; в) дерево по чавуну, f=0,45; г) гума по чавуну, f=0,5. |
4. Вказати формулу для розрахунку діапазону регулювання зображеного варіатора:
а)
|
5. Вказати основні недоліки фрикційних передач: а) складність конструкції; б) велике навантаження на опори; в) ковзання в передачі; г) низька вартість і доступність матеріалів. |
6. Вибрати формулу для розрахунку фрикційної передачі на міцність: а) |
7. Вказати явище, яке не пов’язане з ковзанням у фрикційних передачах: а) буксування; б) пружні деформації в зоні контакту; в) неспівпадіння швидкостей поверхонь, що труться; г) деформація валів. |
8. Вибрати вираз для визначення величини ρзв у формулі для розрахунку циліндричної фрикційної передачі:
а)
|
9. За якою з наведених формул можна визначити точне значення передавального відношення зображеної передачі:
а)
;
б)
;
в)
;
г)
.
|
10. Вибрати спосіб збільшення динамічного коефіцієнта тертя в циліндричній фрикційній передачі (див рис. до завдання 9): а) підвищення твердості поверхонь; б) використання мастильного матеріалу; в) збільшення площі контакту; г) збільшення сили притискання котків. |
11. Вказати основний недолік фрикційних передач: а) необхідність регулювання; б) великі втрати мастильного матеріалу; в) зношування робочих поверхонь; г) нестабільне передавальне відношення. |
12. Як зміниться навантажувальна здатність циліндричної фрикційної передачі при заміні ведучого колеса зі сталі на колесо з гумовим покриттям, якщо: ведене колесо сталеве. При цьому зусилля притискання не змінюється. Динамічний коефіцієнт тертя: сталь по сталі – 0,15; гума по сталі – 0,45: а) зменшиться у 2 рази; б) збільшиться в 3 рази; в) зменшиться в 3 рази; г) не зміниться. |
13. Вибрати вираз який використовується у формулі для розрахунку на міцність циліндричної фрикційної передачі для визначення q:
а)
|
14. Який з наведених варіаторів дозволить отримати реверсне обертання вихідного вала при односторонньому обертанні веденого вала:
а)
багатодисковий; б)
лобовий; в)
торовий; г)
двоконусний.
|
15. Чому фрикційні передачі з безпосереднім контактом не використовують в точних механізмах токарних верстатів: а) із-за низького ККД; б) із-за нагрівання передачі; в) із-за несталого передавального відношення; г) із-за великої ваги. |
16. Яка основна причина виходу з ладу фрикційних передач: а) зношування робочих поверхонь; б) розтріскування котків; в) згин валів; г) заклинювання підшипників. |
17. Як необхідно змінити зусилля притискання пружини, якщо при незмінній потужності замінити сталевий ведучий коток на коток з дерев’яним покриттям? Динамічний коефіцієнт тертя: сталь по сталі (чавуну) ƒ= 0,15; дерево по чавуну ƒ= 0,45: а) збільшити в 1,5 раза; б) збільшити в 3 рази; в) зменшити в 2 рази; г) зменшити в 3 рази. |
18. Вибрати формулу для розрахунку діапазону регулювання зображеного варіатора:
а)
|
19. Визначити мінімальне потрібне зусилля пружини, якщо: обертовий момент на валу передачі 15 Нм; діаметр колеса 350 мм; матеріал коліс – сталь; передача працює із змащенням, ƒ= 0,01:
а)
8571 Н; б)
877 Н; в)
4285 Н; г)
85,7 Н.
|
20. Визначити мінімальне необхідне зусилля притискання коліс, якщо: обертовий момент фрикційної передачі 25 Н·м; діаметр колеса 380 мм; матеріали коліс сталь і чавун; передача працює без мастила; ƒ= 0,15: а) 19,7 Н; б) 877 Н; в) 500 Н; г) 263,1 Н. |
21. Визначити колову силу на колесі Ft, якщо: сила притискання котків фрикційної передачі 1,2 кН; матеріали поверхонь – сталь та чавун; коефіцієнт третя 0,15; коефіцієнт запасу зчеплення, f=1,25:
а)
300 Н; б)
180 Н; в)
144 Н;
г)
288 Н.
|
22. Визначити діапазон регулювання зображеного варіатора, якщо: r1=25 мм; r2min=68 мм; r2max= 120 мм:
а)
0,57; б)
1,76; в)
2,72; г)
4,8.
|
23. Визначити діапазон регулювання наведеного варіатора, якщо: R1= 60 мм; R2= 120 мм:
а)
2; б)
3; в)
4; г)
6.
|
24. Визначити розрахункову колову силу на колесі Ft, якщо: сила притискання котків у фрикційній передачі 1500 Н; матеріали поверхонь – текстоліт і сталь; передача суха ƒ= 0,25; коефіцієнт запасу зчеплення 1,25: а) 1200 Н; б) 300 Н; в) 375 Н; г) 600 Н. |
25. Визначити обертовий момент на валу фрикційної передачі, якщо: матеріал поверхонь – сталь; зусилля пружини 2 кН; радіус колеса 0,05 м; суха передача, ƒ= 0,15:
а)
500 Нм; б)
350 Нм; в)
35 Нм;
г)
15 Нм.
|
Розділ 9
ПАСОВІ ПЕРЕДАЧІ
Мати уяву про пружнє ковзання паса, зусилля і напруження в пасі при передачі обертового моменту.
Знати типи пасів і шківів; геометричні характеристики пасових передач, формули для розрахунку передавального відношення, міжосьової відстані передачі, довжини паса; знати основи розрахунку плоскопасових і клинопасових передач за тяговою здатністю; формули для визначення зусиль натягу гілок паса; формули для визначення напружень в поперечних перерізах паса.
Уміти користуватися таблицями стандартів для вибору пасів передачі.
Уміти користуватися кривою ковзання і ККД паса для визначення зведеного корисного напруження в пасі; знати позначення та фізичний зміст коефіцієнтів у формулі для визначення допустимого корисного напруження.
Пасова передача – фрикційна передача (навантаження передається силами тертя) за допомогою гнучкого зв’язку (пружнього паса).
Пасова передача застосовується для з’єднання валів, розташованих на значній відстані один від одного (рис. 9.1).
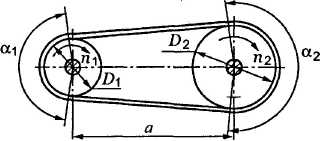
Рис. 9.1. Схема для розрахунку пасової передачі
Класифікація пасових передач
У залежності від форми поперечного перерізу паса передачі поділяються на плоскопасові (рис. 9.2, а), клинопасові (рис. 9.2, б), поліклинові (рис. 9.2, в) і з круглим пасом (рис. 9.2, г) та інші профілі.
У залежності від розташування валів в просторі розрізняють:
передачі з паралельними валами: відкриті (рис. 9.3, а), перехресні (рис. 9.3, б);
передачі із перехресними валами, – напівперехресні (рис. 9.3, в);
передачі з осями валів, що перетинаються – кутові (рис. 9.3, г).
Клинопасову передачу, в основному, застосовують як відкриту (див. рис. 9.3, а).
Попередній натяг паса необхідний для нормальної роботи передачі. Натяг паса може створюватися за рахунок переміщення одного зі шківів, за рахунок натяжних роликів (рис. 9.3, д) або шляхом встановлення двигуна на плиті, що коливається.
Клинопасова передача володіє більшою тяговою здатністю, вимагає меншого натягу, менше навантажує опори валів, допускає менші кути охоплення, використовується при великих передавальних відношеннях і менших міжосьових відстаней (табл. Д12).
Клинові і поліклинові паси виконують нескінченними. Навантаження несе корд або складена в декілька шарів тканина.
Клинові паси випускають трьох видів: нормального перерізу, вузькі і широкі. Широкі паси призначені для варіаторів.
Поліклинові паси – паси з високоміцним кордом і внутрішніми повздовжніми клинами, що входять в канавки на шківах. Вони гнучкіші, ніж клинові, забезпечують більшу сталість передавального числа.
Розміри поліклинових пасів див. в табл. Д13.
Геометричні і кінематичні залежності пасової передачі
Розглянемо відкриту передачу (див. рис. 9.1).
Міжосьова
відстань передачі з плоским пасом
![]() .
.
Міжосьова
відстань передачі клиновим пасом
визначається з умови
![]() ,
де h
– висота паса.
,
де h
– висота паса.
Розрахункова
довжина паса:![]() .
.
Міжосьова відстань в залежності від довжини паса і діаметра шківів:
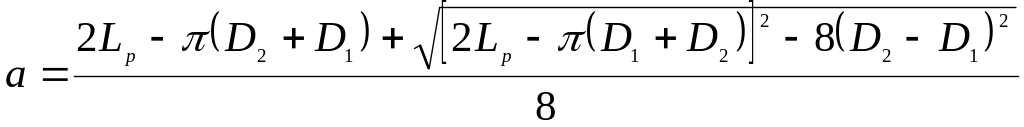 .
.
Рис. 9.2. Типи пасових передач: а – плоскопасова; б – клинопасова;
в – поліклинова; г – з круглими пасами
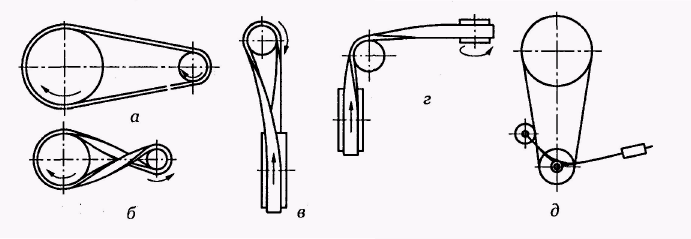
Рис. 9.3. Пасові передачі: а – відкрита; б – перехресна;
в – напівперехресна; г – кутова; д – відкрита з натяжним пристроєм
Кут
охоплення на малому шківі
![]() .
.
Передавальне відношення:
![]() ,
,
де ε – коефіцієнт ковзання в передачі, при нормальній роботі ε = 0,01...0,02.
Наближено
можна приймати:
![]() .
.
Сили натягу в пасі
Сила натягу ведучої гілки паса (рис. 9.4) при передачі навантаження:
![]() .
.
Сила натягу веденої гілки паса:
![]() ,
,
де Ft – колова сила, що передається.
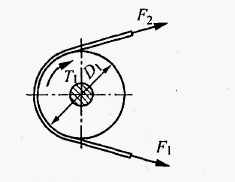
Рис. 9.4. Сили натягу в пасі
Попередній натяг, який створюють сили тертя між шківом і пасом:
![]() ,
,
де σ0 – напруження від попереднього натягу; для плоских гумотканевих пасів σ0 = 1,8 МПа, для стандартних клинових σ0 = 1,2... 1,5 МПа.
При
русі в пасі додатково виникає сила
натягу від відцентрових сил
![]() (суттєво
впливає при швидкості 20 м/с), де ρ
– густина матеріалу паса; А
– площа поперечного перерізу паса.
(суттєво
впливає при швидкості 20 м/с), де ρ
– густина матеріалу паса; А
– площа поперечного перерізу паса.
Таким чином, натяг в гілках паса різний:
![]() .
.
Напруження в пасі
При
роботі на холостому ході (без передачі
навантаження) обидві гілки паса
натягнуті однаково. При передачі
корисного навантаження натяг
гілок паса міняється. Напруження від
попереднього натягу
![]() .
Корисне напруження в пасі
.
Корисне напруження в пасі
![]() визначається від колової сили, що
передається. Значенням k
оцінюють тягову здатність передачі.
визначається від колової сили, що
передається. Значенням k
оцінюють тягову здатність передачі.
Напруження у ведучій і веденій гілках при передачі навантаження:
![]() .
.
При охопленні пасом шківів в пасі виникають напруження згину, які залежать від діаметрів шківів передачі.
На практиці значення напруження згину на малому шківі обмежується заданням мінімального діаметру шківа Dmin.
При коловому русі паса на кожен його елемент діють елементарні відцентрові сили, додатково розтягуючі пас, що веде до виникнення напруження σV.
Таким чином, при русі паса напруження в елементах паса змінюється (рис. 9.5).
Найбільше значення напруження має у момент набігання паса на менший шків, найменше – в момент набігання на більший шків; це явище викликає пружнє ковзання паса на шківах.
При русі на ведучому шківі пас укорочується, а на веденому подовжується, пас ковзає на ведучому шківі.
Необхідно відрізняти пружнє ковзання і буксування. Пружнє ковзання має місце при будь-якому навантаженні, буксування – лише при перевантаженні.
![]() ;
;
![]() ;
;
![]() ;
;
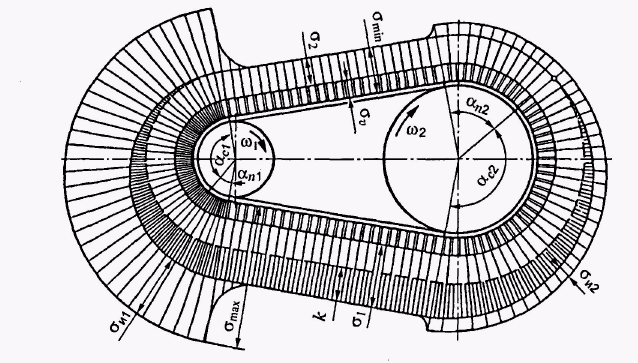
Рис. 9.5. Напруження в пасі при передачі корисного навантаження
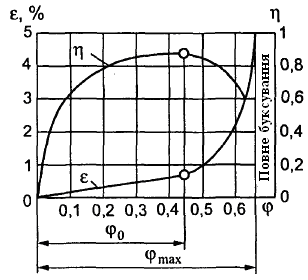
Рис. 9.6. Крива ковзання та К.К.Д. пасової передачі
![]() ;
;
![]() ;
;
![]() ,
де δ
– товщина паса; E
– модуль пружності.
,
де δ
– товщина паса; E
– модуль пружності.
Криві ковзання паса
Крива ковзання (рис. 9.6) встановлює зв’язок між корисним навантаженням і відносним ковзанням ε в передачі, φ – коефіцієнт тяги (відносне навантаження). При підвищенні коефіцієнта тяги від нуля до критичного значення φ0 в передачі відбувається лише пружнє ковзання, одночасно із збільшенням φ зростає і ККД η. При подальшому збільшенні коефіцієнта тяги робота стає нестійкою (часткове буксування). Значення φ встановлені для кожного типу паса. Робоче навантаження рекомендується вибирати ближчим до критичного значення.
Розрахунок паса за тяговою здатністю
Розрахунок плоскопасової передачі зводиться до визначення необхідної площі поперечного перерізу паса. Зведене корисне напруження:
![]() .
.
Умови експлуатації паса враховуються введенням коефіцієнта.
Допустиме корисне напруження:
![]() ,
,
де Сα – коефіцієнт, що враховує вплив кута охоплення на меншому шківі; Cv – швидкісний коефіцієнт, що враховує вплив відцентрових сил; Cθ – коефіцієнт розташування передачі в просторі; Ср – коефіцієнт режиму навантаження.
Остаточно визначаємо:
![]() .
.
Для передач клиновими і поліклиновими пасами слід вибрати відповідний пас за таблицями або за допомогою графіків і визначити число пасів клинопасової передачі (табл. Д12 і Д13).
Переріз паса вибирають в залежності від обертового момента на швидкохідному валу або потужності (рис. 9.7, а). Мінімальні діаметри шківів вибирають за таблицею Д12 Додатка. При можливості слід уникати мінімальних значень діаметрів шківів і мінімальних значень міжосьових відстаней, оскільки це зменшує довговічність паса.
Для вибраного паса визначають номінальну потужність, яка передається одним пасом.
Визначають розрахункові коефіцієнти, які враховують умови експлуатації паса.
Визначають число пасів в комплекті для передачі заданої потужності:
![]() ,
,
де CL – коефіцієнт довжини паса; Р0 – номінальна потужність, яка передається одним пасом; РP – потужність, яка передається одним пасом в умовах експлуатації; CZ – коефіцієнт, що враховує нерівномірність розподілу навантаження між пасами, CZ = 1 ...0,85.
а б
Рис. 9.7. Типи перерізів клинових пасів та їх розміри: а – номограма для вибору перерізу клинових пасів; б – розміри перерізів клинових пасів
Оцінка пасових передач
Переваги пасових передач:
пасова передача пом’якшує поштовхи й удари – може демпферувати коливання;
пасова передача може служити запобіжною ланкою при перевантаженнях;
пасова передача може використовуватися для безступінчастого регулювання швидкості (див. рис. 2.3, д);
можливість передачі руху на значні відстані (до 15 м і більше).
Недоліки пасових передач:
великі габаритні розміри;
неможливо забезпечити сталість передавального відношення;
недостатня довговічність паса;
значні навантаження на опори, особливо в плоскопасових передачах.
У високонавантажених передачах застосовують передачі із зубчастим пасом – пасом із зубцями на внутрішній поверхні. Передача працює за принципом зачеплення паса зі шківом.
Тема: Пасові передачі
1. Назвати передачу, зображену на рисунку:
а
б
в
г
а) клинопасова; б) плоскопасова; в) напівперехресна; г) перехресна. |
2. Вказати основні переваги плоскопасових передач в порівнянні з клинопасовими: а) простота; б) плавність ходу; в) великі навантаження на опори; г) використання в передачах з непаралельними валами. |
3. Вибрати формулу для розрахунку напруження в пасі правіше точки С:
а)
|
4. Вибрати
формулу для розрахунку напруження в
точці А паса (див. рис. до питання 3),
якщо:
а) ; б) ; в) ; г) . |
5. Що враховує
коефіцієнт
а) вплив кута охоплення пасом шківа; б) вплив відцентрових сил; в) вплив динамічності навантаження; г) розташування передачі в просторі. |
6. Що враховує
коефіцієнт
а) вплив кута охоплення пасом шківа; б) вплив відцентрових сил; в) вплив динамічності навантаження; г) розташування передачі в просторі. |
7. Яке основне призначення перехресних пасових передач:
б
а
г
в
а) збільшення довговічності; б) збільшення міжосьової відстані; в) обертання валів назустріч один одному; г) збільшення кута охоплення. |
8. Визначити основні переваги зображених передач в порівнянні з плоскопасовими передачами:
а
б
в
а) менш жорсткі вимоги до встановлення; б) більша довговічність; в) більша жорсткість паса; г) більша несуча здатність при однаковому попередньому натягу паса. |
9. Вказати найбільш навантажену точку паса зображеної передачі, якщо змінити напрям обертання шківа на зворотній:
а)
A;
б)
B;
в)
С; г)
D.
|
10. Що розуміють під пружнім ковзанням паса в передачі:
а) розтяг при передачі заданого навантаження; б) ковзання паса на шківі при перевантаженні; в) проковзування на шківі через зменшення тертя; г) циклічні зміни швидкості паса на шківах через зміни його натягу. |
11. Зображені деякі з конструкцій клинових пасів. У чому основне призначення прорізів на внутрішній поверхні паса 3:
а) зменшення маси паса; б) підвищення тягової здатності; в) збільшення тертя між пасом і шківом; г) зменшення напружень згину в пасі. |
12. Вказати основні переваги паса 3 над пасом 2:
а) менша вага; б) рівномірна витяжка, порівняно з багаторядними передачами; в) більший коефіцієнт тертя; г) менший діаметр шківа. |
13. Проаналізувати криву ковзання та ККД паса, визначити що відбувається з передачею при роботі в зоні φ>0,6:
а) ведений шків зупиняється; б) колова сила рівна силі тертя; в) ведучий шків зупиняється; г) виникає часткове буксування, тертя збільшується. |
14. У чому полягає втомне руйнування паса: а) стирається робоча поверхня; б) виникають тріщини на поверхні паса; в) перетираються тканини, розшаровується пас; г) обвуглюється гума. |
15. Визначити коефіцієнт ковзання в пасовій передачі, якщо: діаметр ведучого шківа d1=60 мм; діаметр веденого шківа d2=150 мм; частота обертання ведучого вала n1=1000 хв-1; веденого вала n2 =390 хв-1:
а)
0,04; б)
0,025; в)
0,25; г)
0,015.
|
16. Визначити натяг ведучої гілки паса F1, якщо: напруження від попереднього натягу 1,8 МПа, потужність що передається 9,9 кВт: діаметр ведучого шківа 200 мм; площа перерізу паса 375 мм2, кутова швидкість 90 с-1: а) 0,675 кН; б) 1,225 кН; в) 1,10 кН; г) 1,775 кН. |
17. Визначити діаметр меншого шківа, якщо: діаметр більшого шківа d2=210 мм; частота обертання ведучого вала n1=945 хв-1, частота обертання веденого вала n2= 540 хв-1: а) 100 мм; б) 112 мм; в) 120 мм; г) 140 мм. |
18. Розрахувати зведене корисне напруження за визначеним по графіку оптимальним значенням коефіцієнта тяги та напруження від попереднього натягу паса 1,55 МПа:
а)
1,71 МПа; б)
1,305 МПа;
в)
0,675 МПа;
г)
1,395 МПа.
|
19. Визначити кутову швидкість веденого шківа пасової передачі, якщо: діаметри шківів d1=80 мм та d2=250 мм; лінійна швидкість паса 6 м/с; коефіцієнт ковзання в передачі 0,03: а) 150 с-1; б) 76,5 с-1; в) 3,125 с-1; г) 46,56 с-1. |
20. Визначити фактичне передавальне відношення пасової передачі, якщо: діаметр ведучого шківа d1=315 мм; діаметр веденого шківа d2=785 мм; коефіцієнт ковзання в передачі 0,02:
а)
0,4; б)
2,49; в)
2,09; г)
2,54.
|
21. Потужність на ведучому валі пасової передачі 20 кВт, частота обертання 800 хв-1. Вибрати тип перерізу клинового паса та його розміри:
а)
b=13, h=8;
б)
b=17
h=10,54
в)
b=22
h=12,5;
г)
b=32
h=19. |
22. Визначити колове зусилля на веденому шківі передачі, якщо: потужність на ведучому валу 2,8 кВт; кутова швидкість веденого шківа 70 с-1; ККД передачі 0,95; діаметр веденого шківа 200 мм: а) 190 Н; б) 270 Н; в) 380 Н; г) 400 Н. |
23. Визначити зведене корисне напруження для паса, використовуючи криву ковзання ККД та оптимальний коефіцієнт тяги, якщо напруження від попереднього натягу паса 2,7 МПа:
а)
3,24 МПа; б)
2,26 МПа;
в)
1,788 МПа; г)
5,52 МПа.
|
24. Визначити дійсну частоту обертання вихідного вала, якщо: частота обертання ведучого шківа 960 хв-1; діаметри шківів передачі d1=120 мм і d2= 360 мм; коефіцієнт ковзання 0,03: а) 33 хв-1; б) 120 хв-1; в)240 хв-1; г) 310,4 хв-1. |
25. Визначити натяг веденої гілки паса в робочому режимі пасової передачі, якщо: напруження від попереднього натягу паса 1,5 МПа; розміри перерізу: b=70 мм, δ=7 мм; потужність на ведучому валу 4,5 кВт; кутова швидкість 75 с-1; діаметр ведучого шківа 260 мм:
а)
306 Н; б)
520 Н; в)
735 Н;
г)
428,5 Н.
|
Розділ 10
ЛАНЦЮГОВІ ПЕРЕДАЧІ
Знати основні параметри, кінематику і геометрію ланцюгових передач; типи ланцюгів і зірочок, їхню порівняльну оцінку; позначення ланцюгів за стандартом.
Уміти підібрати тип ланцюгової передачі за відповідним довідковим матеріалом.
Уміти підібрати ланцюг і розрахувати ланцюгову передачу на довговічність, виходячи із зносостійкості шарнірів ланцюга.
Знати позначення, фізичний зміст коефіцієнтів, уміти вибирати їх, виходячи із заданих умов експлуатації.
Ланцюгова передача – передача зачепленням гнучким зв’язком. Гнучкий зв’язок утворює шарнірний ланцюг, який охоплює зубчасті зірочки (рис. 10.1).
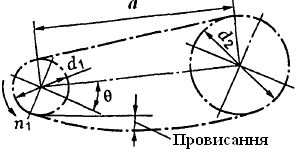
Рис. 10.1. Схема ланцюгової передачі
Традиційно ланцюгові передачі застосовують в сільськогосподар-ських і будівельно-дорожніх машинах, в хімічному машинобудуван-ні, верстатобудуванні і підйомно-транспортних пристроях.
Оцінка ланцюгових передач
Переваги ланцюгових передач:
передача руху зачепленням, а не тертям дозволяє реалізувати більші передавальні числа, ніж за допомогою паса;
практично не потрібний натяг ланцюга, отже, зменшується навантаження на вали й опори;
відсутність ковзання і буксування забезпечує сталість середнього передавального відношення;
ланцюги можуть стійко працювати при менших міжосьових відстанях;
ланцюгові передачі добре працюють в умовах частих пусків і гальмувань;
ланцюгові передачі мають високий ККД.
Недоліки ланцюгових передач:
знос ланцюга при недостатньому змащуванні і поганому захисті від бруду;
складний догляд за передачею;
підвищена вібрація і шум;
порівняно із зубчастими передачами підвищена нерівномірність руху;
спадання ланцюга в результаті його видовження, внаслідок подовження пластин і зносу шарнірів.
Класифікація ланцюгових передач
Сьогодні застосовують шарнірні роликові, втулкові (рис. 10.3, а) і зубчасті (рис. 10.3, б) ланцюги. У роликових ланцюгах зачеплення ланцюга із зірочкою здійснюється через ролик: довговічність ланцюга зростає, але й зростає маса і вартість ланцюга.
Ланцюги бувають однорядними і багаторядними.
Зубчасті ланцюги набирають із пластин; велике значення має конструкція шарніра. У конструкцію входить напрямна пластина, яка запобігає спаданню ланцюга із зірочки. Порівняно із втулковими зубчасті ланцюги працюють плавніше, забезпечують велику кінематичну точність, мають високий ККД, але їх маса і вартість значно вищі.
Форма профілю зубця зірочки залежить від конструкції і розмірів ланцюга. Зірочка для втулкового і роликового ланцюга показана на рис. 10.2, а, зірочка для зубчастого ланцюга – на рис. 10.2, б.
Геометричні і кінематичні параметри ланцюгової передачі
Основний геометричний параметр ланцюга – крок t, мм (див. рис. 10.3).
Оптимальна міжосьова відстань а = (30...50)t. Довжина ланцюга в кроках:
![]() ,
,
де z1 і z2 – число зубців зірочок.
Р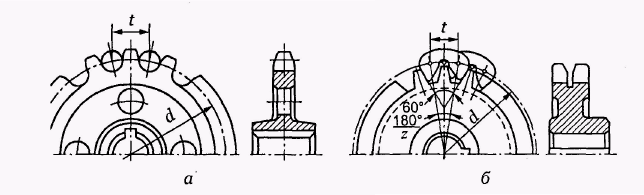 ис.
10.2. Типи зірочок для ланцюгових передач:
а
– для втулкового і роликового ланцюга;
б
– для зубчастого ланцюга
ис.
10.2. Типи зірочок для ланцюгових передач:
а
– для втулкового і роликового ланцюга;
б
– для зубчастого ланцюга
Р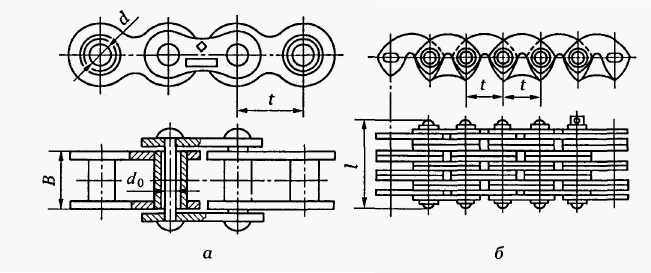 ис.
10.3. Типи ланцюгів: а
–
втулкові; б
– зубчасті
ис.
10.3. Типи ланцюгів: а
–
втулкові; б
– зубчасті
Число зубців малої зірочки вибирають із співвідношення:
![]() ,
,
тоді
![]() .
.
Кінцеве значення міжосьової відстані:
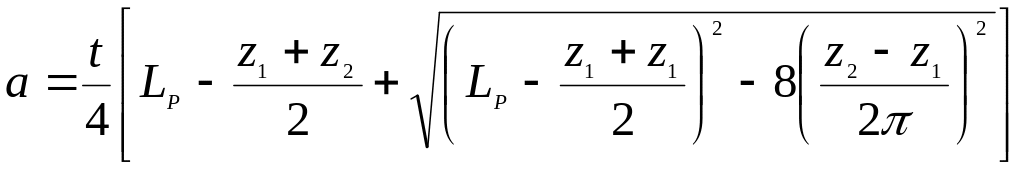 .
.
Діаметр
ділильного кола зірочки:
![]() .
.
Передавальне число: .
Передавальне відношення передачі не можна визначати як відношення діаметрів ділильних кіл зірочок. У межах одного оберта зірочки передавальне відношення не залишається сталим, тому враховують середню швидкість ланцюга, м/с:
![]() ,
,
де ω, z – кутова швидкість і число зубців зірочки.
Критерії працездатності і розрахунок ланцюгової передачі
При проектному розрахунку попередньо визначають крок ланцюга за формулою:
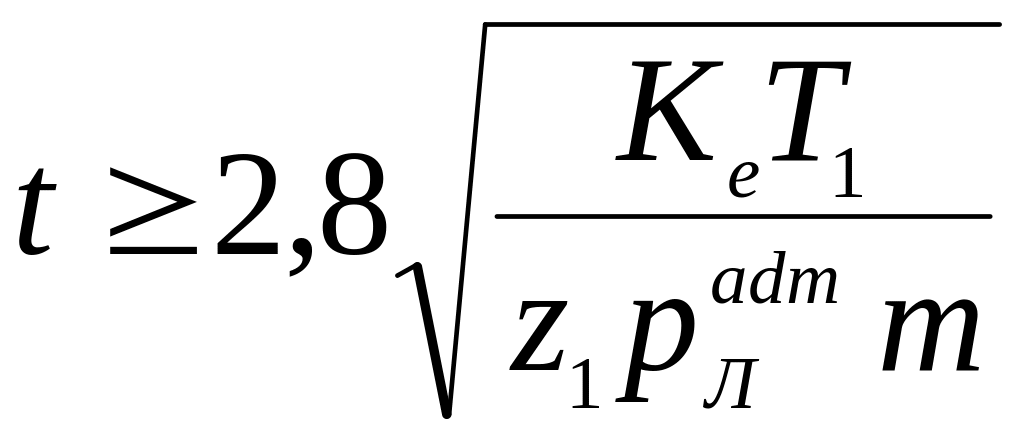 ,
,
де Ке
– коефіцієнт експлуатації,
![]() ;
КД
– коефіцієнт динамічності; Кс
– коефіцієнт способу змащування
передачі; K0
– коефіцієнт нахилу передачі до
горизонту; Kрег
– коефіцієнт способу регулювання;
Кp
– коефіцієнт режиму навантаження; Т1
– обертовий момент на ведучій зірочці;
;
КД
– коефіцієнт динамічності; Кс
– коефіцієнт способу змащування
передачі; K0
– коефіцієнт нахилу передачі до
горизонту; Kрег
– коефіцієнт способу регулювання;
Кp
– коефіцієнт режиму навантаження; Т1
– обертовий момент на ведучій зірочці;
![]() – середнє допустиме питоме навантаження
в шарнірі; m
– число рядів ланцюга;
– мінімальне число зубців ведучої
зірочки роликового ланцюга.
– середнє допустиме питоме навантаження
в шарнірі; m
– число рядів ланцюга;
– мінімальне число зубців ведучої
зірочки роликового ланцюга.
Після підбору ланцюга за стандартом (табл. Д14) вибрана передача перевіряється на зносостійкість за формулою:
![]() ,
,
де
Ft
– колова
сила,
![]() ;
;
![]() ;
А
– площа проекції
опорної
поверхні
шарніра,
;
А
– площа проекції
опорної
поверхні
шарніра,
![]() ;
d0
– діаметр осі; В
– довжина втулки (див. рис. 10.3, а).
;
d0
– діаметр осі; В
– довжина втулки (див. рис. 10.3, а).
Сили в ланцюговій передачі
У ланцюговій передачі ведуча і ведена гілки натягнуті по-різному. Натяг ведучої гілки працюючої передачі:
![]() ,
,
де Ft – колова сила, яка передається ланцюгом; F0 – попередній натяг від провисання веденої гілки ланцюга; FV – натяг від відцентрових сил.
Попередній натяг незначний і складає декілька відсотків від Ft; в тихохідних передачах можно нехтувати і натягом від відцентрових сил.
Допустимі питомі навантаження в шарнірі, що гарантує нормальну роботу протягом прийнятого терміну служби, визначається за табл. 10.1.
Таблиця 10.1
Допустимі питомі навантаження в шарнірі ланцюга
-
ω, с-1
, МПа при кроці ланцюга t, мм
12,7…25,4
19,05…25,4
31,75…38,1
4,45…50,8
5,2
21
42
63
84
105
126
167
34,3
30,9
28,1
25,7
23,7
22,0
20,6
18,1
34,3
29,4
25,7
22,9
20,6
18,6
17,2
14,7
34,3
28,1
23,7
20,6
18,1
16,3
14,7
-
34,3
25,7
20,6
17,2
14,7
-
-
-
Позначення роликових ланцюгів: перша цифра – число рядів; друга цифра – крок, мм; третя – руйнівне навантаження, пропорційне 10 Н; четверта – виконання по ширині.
Наприклад, ПР-12,7-1820-1: роликовий ланцюг, однорядний, крок 12,7 мм, руйнівне навантаження 18200 Н, першого виконання по ширині.
Тема: Ланцюгові передачі
1. Які основні переваги ланцюгових передач у порівнянні із зубчастими:
а) простота виготовлення; б) знижена віброактивність і шум; в) необмежена міжосьова відстань; г) менша вимога до точності встановлення. |
2. У чому основна перевага ланцюга (а) в порівнянні з ланцюгом (б):
а) в збільшенні зношування шарнірів; б) в зменшенні рухомості шарнірів; в) в зменшенні ваги; г) ланцюги ідентичні. |
3. Що
враховує і як розраховується
а)
корисне навантаження,
|
4. Які основні переваги ланцюгових передач у порівнянні із пасовими:
а) менше навантаження на вали; б) можливість передавати більший обертовий момент; в) змащування значно покращує роботу; г) значні поштовхи й удари. |
5. Для якого ланцюга підходить зображена зірочка:
а) для втулкового; б) для роликового; в) для зубчастого; г) для роликового із зігнутими пластинами. |
6. Як
розрахувати величину А в формулі для
передачі із роликовим
(втулковим) ланцюгом (dо
–
діаметр валика; Во
–
довжина втулки; D
– діаметр
ролика)
а)
|
7. Як називається коефіцієнт К у формулі для проектного розрахунку кроку ланцюгової передачі
а) температурний коефіцієнт; б) коефіцієнт швидкості; в) коефіцієнт експлуатації; г) коефіцієнт запаса міцності. |
8. Які основні недоліки ланцюгових передач у порівнянні з зубчастими:
а) чутливість до точності установки; б) простота зміни передавального відношення; в) нестале передаточне відношення; г) підвищення вібрації і шум. |
9. Вказати основне призначення ролика 1 в наведеному ланцюгу (2 – втулка; 3, 5 – внутрішні та зовнішні пластини; 4 – валик):
а) зменшення зносу втулки 2; б) зменшення зносу ролика 1; в) зменшення зносу валика 4; г) зменшення кроку ланцюга. |
10. Який основний недолік ланцюгової передачі із зубчастим ланцюгом:
а) низька навантажувальна здатність; б) нерівномірність ходу; в) підвищені вимоги до встановлення; г) висока вага і вартість. |
11. Які основні причини виходу з ладу ланцюгових передач: а) збільшення кроку ланцюга; б) корозія металу; в) провисання ланцюга; г) знос і руйнування деталей. |
12. Що враховує параметр m у формулі для проектного розрахунку кроку ланцюгової передачі
а) число робочих змін; б) характер навантаження; в) число рядів ланцюга; г) тип ланцюга. |
13. Який основний недолік ланцюгових передач у порівнянні з пасовими: а) мала довговічність шарнірів; б) обмежена несуча здатність; в) віброактивність і удари; г) стала швидкість ланцюга. |
14. Як впливає на роботу ланцюгової передачі вибір збільшеного кроку ланцюга:
а) знижує навантажувальну здатність; б) підвищує навантажувальну здатність; в) знижує рівень шуму; г) знижує витягування ланцюга. |
15. Для якого ланцюга підійде зображена зірочка:
а) для роликового однорядного; б) для роликового дворядного; в) для зубчастого однорядного; г) для фасонно-ланкового. |
16. Визначити передавальне відношення ланцюгової передачі, якщо: число зубців меншої зірочки 21; число зубців більшої зірочки 83; діаметр зірочок 81,4 та 362,8 мм: а) 4,45; б) 3,95; в) 3,5; г) 2,95. |
17. Визначити діаметр ділильного кола зірочки ланцюга ПР-31,75-89, якщо число зубців 25: а) 25,4 мм; б) 63,5 мм; в) 125,4 мм; г) 254,4 мм. |
18. Визначити діаметр ділильного кола зірочки ланцюгової передачі, якщо: число зубців зірочки 83; підібрано ланцюг ПР-25,4-60: а) 68,7 мм; б) 135,4 мм; в) 435 мм; г) 672 мм. |
19. Визначити колове зусилля, яке передає ланцюг, якщо: потужність на ведучому валу передачі 8,5 кВт: діаметр ведучої зірочки 100 мм; кутова швидкість веденого вала 18с-1; передавальне відношення 4: а) 800 Н; б) 1180 Н; в) 2360 Н; г) 4722 Н. |
20. Визначити середнє передавальне відношення, якщо: число зубців зірочки z1=24; z2=60; діаметри зірочок d1=255 мм; d2= 635 мм: а) 2,5; б) 3,5; в) 2,6; г) 10,6. |
21. Визначити діаметр ділильного кола зірочки ланцюгової передачі, якщо: підібрано ланцюг 2ПР-12,7-31,8: число зубців 21: а) 382,8 мм; б) 86 мм; в) 109 мм; г) 238 мм. |
22. Визначити передавальне відношення передачі, якщо: число зубців зірочки z1=23, z2=70, діаметри ділильних кіл зірочок d1=145 мм, d2=406 мм:
а) 2,79; б) 3,04; в) 0,33; г) 6,3. |
23. Визначити діаметр ділильного кола зірочки ланцюгової передачі, якщо: число зубців 26; підібрано ланцюг ПР-19,05-31,8: а) 44 мм; б) 86 мм; в) 158 мм; г) 206 мм. |
24. Визначити діаметр ділильного кола зірочки для ланцюгової передачі, якщо: число зубців зірочки 45; передавальне відношення 1,55; підібрано ланцюг 2ПР-50,8-453: а) 475 мм; б) 264 мм; в) 728 мм; г) 600,5 мм. |
25. Визначити силу, яка діє на ведучу гілку ланцюга, якщо: потужність на ведучому валу передачі 4,5 кВт; частота обертання ведучого вала 750 хв-1, натяг від провисання веденої гілки 68 Н; натяг від відцентрових сил 58 Н; діаметр ведучої зірочки 250 мм: а) 458,4 Н; б) 126 Н; в) 584,4 Н; г) 710,4 Н. |
Частина 2
ВАЛИ ТА ОСІ. ПІДШИПНИКИ. ЗАГАЛЬНІ
ВІДОМОСТІ ПРО РЕДУКТОРИ. МУФТИ
Розділ 11
ВАЛИ ТА ОСІ
Знати назви і призначення елементів конструкції валів і осей: цапф, шийок, галтелів, фасок і таке інше.
Знати марки матеріалів, які при цьому застосовуються; причини виходу з ладу і критерії працездатності валів і осей.
Уміти провести проектний і перевірний розрахунки валу та осі.
Вали призначені для передачі обертового моменту і підтримки розташованих на них деталей (рис. 11.1, а); осі, підтримуючи розташовані на них деталі, обертового моменту не передають.
Осі бувають обертальними (рис. 11.1, б) і нерухомими (рис. 11.1, в).
Рис. 11.1. Вали та осі: а – вал; б – вісь, що обертається; в – нерухома вісь; 1– цапфа; 2 – шийка
Виходячи з розрахунку на міцність для зручності встановлення деталей вали виконують ступінчастими. Перехідні ділянки валів між двома ступенями різних діаметрів виконують такими способами:
- із рівцем для виходу шліфувального круга (рис. 11.2, а), рівці виконують завширшки (3…5) мм і глибиною (0,3…0,5) мм;
- із галтеллю постійного радіуса (рис. 11.2, б), радіус галтелі вибирають меншим від радіуса заокруглення або фаска деталі, що розміщується на валу (рис. 11.3, в);
- із галтеллю спеціальної форми (рис. 11.3, г) або із змінним радіусом кривини (рис. 11.3, д).
Рис. 11.2. Перехідні ділянки вала
Матеріали
Для валів і осей застосовують якісні вуглецеві і леговані сталі.
Вали та осі обробляють на токарних верстатах, посадочні поверхні можуть шліфуватися.
Критерії працездатності і види руйнувань валів і осей
Вали та осі, що обертаються, при роботі сприймають циклічні змінні напруження (рис. 11.3), і частіше всього виходять з ладу в результаті втомних руйнувань.
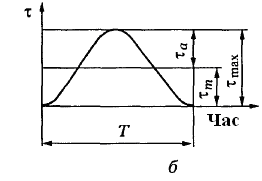
Рис. 11.3. Цикли напружень в перерізі валів: а – симетричний; б – віднулевий; Т – тривалість одного циклу (період)
Основними розрахунковими навантаженнями є обертовий момент (для валів) і згинальний момент.
Основними критеріями працездатності є міцність і жорсткість.
Розрахунок валів
Розрахунок валів проводиться в два етапи: проектний лише під дією обертового моменту і перевірний розрахунок із урахуванням обертового і згинального моментів.
1. Проектний (попередній) розрахунок вала проводять за формулою:
![]() ,
,
де Т
– обертовий момент, d
– діаметр вала;
![]() – допустиме напруження при
крученні
= 20...30 МПа.
– допустиме напруження при
крученні
= 20...30 МПа.
Отримане значення діаметра вала заокруглюють до найближчого більшого розміру з ряду чисел R40 по державному стандарту «Нормальні лінійні розміри» (див. табл. Д7). Форму і розміри вала уточнюють при ескізному проектуванні вала після визначення розмірів коліс, муфт і підшипників, за якими визначають довжину шийок і цапф валу.
Перевірний розрахунок спроектованого вала проводять на опір втомі і на жорсткість.
Попередньо визначають всі конструктивні елементи вала, обробку і якість поверхні окремих ділянок. Складається розрахункова схема вала і наносяться діючі навантаження.
2. Перевірний (уточнений) розрахунок на опір втомі полягає у визначенні розрахункових коефіцієнтів запасу міцності в небезпечних перерізах, виявлених із епюр моментів з урахуванням концентрації напружень.
Приймають, що напруження згину змінюється по симетричному циклу (див. рис. 11.3, а), а напруження кручення – по віднульовому (див. рис. 11.3, б).
Амплітуда цикла зміни напруження згину вала:
![]() ,
,
амплітуда віднульового циклу зміни напруження кручення:
![]() ,
,
де WОC, WР – момент опору згину і кручення перерізів вала, відповідно.
Запас міцності вала:
за нормальними напруженнями
![]() ;
;
за дотичними напруженнями
![]() ,
,
де σ-1 – границя витривалості при розрахунку на згин; τ-1 – границя витривалості при розрахунку на кручення; KσD, KτD – загальний коефіцієнт концентрації напружень при згині і крученні відповідно:
![]() ;
;
![]() ,
,
де Kσ, Kτ – коефіцієнти зниження границі витривалості за рахунок місцевих концентраторів – галтелей, виточок, поперечних отворів, шпонкових пазів (ефективний коефіцієнт концентрації напружень); Kd – коефіцієнт впливу абсолютних розмірів; КF – коефіцієнт впливу обробки поверхні; KV – коефіцієнт зміцнення поверхні; значення перерахованих коефіцієнтів наведені в спеціальній літературі.
Розрахунковий коефіцієнт запасу витривалості в перерізі при сумісній дії згину і кручення:
![]() .
.
Мінімальне допустиме значення коефіцієнта запасу міцності 1,6...2,5.
Розрахунок осей ведуть тільки на згин: при розрахунку нерухомих осей приймають зміни напружень по віднульовому циклі, при розрахунку рухомих – по симетричному.
3. Спрощений перевірний розрахунок на втому проводять в припущенні, що нормальне напруження (згину) і дотичні напруження (кручення) змінюються по симетричному циклі. Одночасна дія обертового і згинального моментів розраховується за гіпотезою найбільших дотичних напружень:
![]() ,
,
де Мзг – сумарний згинальний момент, геометрична сума згинальних моментів у вертикальній і горизонтальній площинах:
![]() .
.
Умова опору втомі:
![]() ,
,
де
σекв
–
еквівалентне напруження в перерізі;
Мекв
– еквівалентний момент в перерізі;
d
– діаметр вала в перерізі;
![]() – допустиме напруження згину
при симетричному циклі зміни напружень.
– допустиме напруження згину
при симетричному циклі зміни напружень.
У більшості випадків обмежуються спрощеним перевірним розрахунком.
У спеціальних випадках використовують колінчасті (непрямі) вали і вали зі змінною формою геометричної осі (гнучкі). Використовують суцільні і порожнисті (з осьовим отвором) вали.
Тема: Вали та осі
1. Серед зображених деталей вказати вал:
а
б
в
г
а) а; б) б; в) в; г) г. |
2. Як називаються елемент деталей 1 (див. рис. до питання 1): а) буртик; б) шийка; в) шпонковий паз; г) галтель. |
3. Яке навантаження враховується при проектному розрахунку вала: а)
згинальний момент Мз
; б)
обертовий момент Т
; в)
еквівалентний момент
|
4. Для чого використовують в техніці зображений на схемі вал:
а) для передачі обертового моменту вздовж своєї осі; б) для підтримки деталей, що обертаються; в) для перетворення зворотно-поступального руху в обертовий; г) для передачі моменту між точками, які міняють своє положення. |
5. При перевірному
розрахунку валів на опір втомі
розраховується коефіцієнт а) концентрацію напружень в місцях вирізів; б) вплив шорсткості поверхонь; в) вплив абсолютних розмірів; г) вплив зміцнення. |
6. Для чого використовують виділений кольором елемент конструкції вал а:
а) для осьової фіксації колеса; б) для центрування колеса на валу; в) для зручності збирання; г) для передачі обертового моменту від вала на колесо чи навпаки. |
7. З якою метою в техніці використовують зображений на схемі вал:
а) для підтримки деталей, які обертаються; б) для передачі обертового моменту вздовж осі вала; в) для перетворення зворотньо-поступального руху в обертовий; г) для передачі моменту між деталями, які міняють своє положення при роботі. |
8. Вибрати формулу для розрахунку на міцність деталі 1:
а)
в)
|
9. При виконанні перевірного розрахунку вала редуктора на витривалість необхідно визначити напруження згину. Вибрати формулу для визначення середнього σm, та амплітудного σа значення напруження: а)
|
10. Серед зображених конструкцій вказати вісь:
а
б
в
г
а) а; б) б; в) в; г) г. |
11. Вказати основний критерій працездатності валів: а) статична міцність при згині; б) опір втомі; в) статична міцність при сумісній дії Мзг та Т ; г) стійкість. |
12. Для яких
перерізів вала (осі) необхідно виконувати
перевірку на жорсткість за
формулою
а) для середнього перерізу; б) для полегшення встановлення деталі на вал; в) для фіксації деталі на валу в осьовому перерізі; г) для передачі обертового моменту з вала на колесо. |
13. Для чого використовують виділений елемент деталі 1:
а) для зниження концентрації напружень; б) для полегшення встановлення деталі на вал; в) для фіксації деталі на валу в осьовому перерізі; г) для передачі обертового моменту з вала на колесо. |
14. При виконанні
перевірного розрахунку вала на опір
втомі визначаються запас міцності
в небезпечному перерізі. При цьому
визначається коефіцієнт:
а) концентрацію напружень в місцях зміни форми; б) розміри поперечного перерізу; в) робочу температуру; г) стан поверхні. |
15. Вибрати цикл зміни напружень, які виникають при роботі в матеріалі осі, що обертається:
б)
а)
в)
г
а) а; б) б; в) в; г) г. |
16. Визначити максимальний згинальний момент в перерізі вала:
а) 132 Нм; б) 146,5 Нм; в) 204 Нм; г) 315,4 Нм. |
17. Розрахунок
валів на опір втоми при крученні
виконують за формулою
а) 70 МПа; б) 35 МПа; в) 17,5 МПа; г) 43,2 МПа. |
18. Визначити діаметр вала, якщо: потужність на валу 5,5 кВт при частоті обертання вала 1000 хв-1, якщо матеріал вала–сталь; допустиме напруження 16 МПа: а) 18 мм; б) 26 мм; в) 36 мм; г) 42 мм. |
19. Для зображеного на схемі вала визначити еквівалентний момент за гіпотезою найбільших дотичних напружень для спрощеного перевірного розрахунку на втому:
а) 269,3 Нм; б) 357 Нм; в) 483 Нм; г) 588 Нм. |
20. Визначити діаметр вала для передачі обертового моменту 103 Н·м, якщо: матеріал вала – сталь; допустиме напруження 12 МПа. Значення діаметра вала заокруглюємо до найближчого стандартного: а) 30 мм; б) 36 мм; в) 45 мм; г) 53 мм. Нормальні лінійні розміри: 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 53; 56; 60; 63; 67…мм. |
21. Визначити максимальний згинальний момент в перерізі зображеного вала:
а) 655 Нм; б) 730 Нм; в) 837 Нм; г) 955 Нм. |
22. Визначити діаметр вихідного кінця веденого вала редуктора, якщо: обертовий момент на вхідному валу 65 Нм; ККД редуктора 0,955; передавальне відношення 4; матеріал вала–сталь; допустимі напруження 20 МПа. Результат діаметра вала заокруглюємо до найближчого стандартного: а) 25 мм; б) 30 мм; в) 40 мм; г) 50 мм. Нормальні лінійні розміри: 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 53; 56…мм. |
23. Визначити діаметр вала в небезпечному перерізі А–А, якщо: діючий в перерізі момент 154 Н·м; матеріал сталь; допустиме напруження 80 МПа. Результат діаметра вала заокруглюємо до найближчого стандартного: а) 20 мм; б) 25 мм; в) 28 мм; г) 45 мм.
Нормальні лінійні розміри: 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 53; 56…мм. |
24. Для зображеного вала визначити максимальний еквівалентний момент за теорією енергії формозміни для спрощеного розрахунку на втому:
а) 55,4 Н; б) 71 Н; в) 88,7 Н; г) 135,5 Нм. |
25. Для зображеного вала визначити еквівалентний момент за гіпотезою найбільших дотичних напружень для спрощеного розрахунку на втому:
а) 440 Нм; б) 462,6 Нм; в) 744 Нм; г) 290,3 Нм. |
Розділ 12
ПІДШИПНИКИ КОВЗАННЯ
Мати уяву про робочий процес підшипників ковзання; про види руйнувань і критерії працездатності. Знати конструкції, матеріали, ККД підшипників, способи змащення.
Знати порядок розрахунку на зносостійкість і теплостійкість. Уміти визначати допустиме навантаження на підшипник із розрахунку на теплостійкість і зносостійкість.
Підшипники забезпечують валам задане положення і можливість обертання в заданому напрямі, із заданою швидкістю і навантаженням при мінімальних втратах на тертя.
Класифікація підшипників ковзання
За конструкцією підшипники ковзання поділяють на роз’ємні і нероз’ємні (рис. 12.1, а, б). За напрямом сприйнятих навантажень підшипники ковзання поділяють на радіальні, які сприймають навантаження, перпендикулярні осі вала (рис. 12.1, а–в) й упорні – для сприйняття навантажень вздовж осі вала (підп’ятник, рис. 12.1, г); іноді підшипники можуть сприймати поєднання радіального і осьового навантаження.
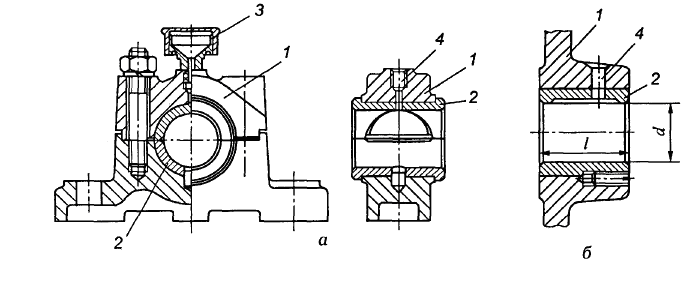
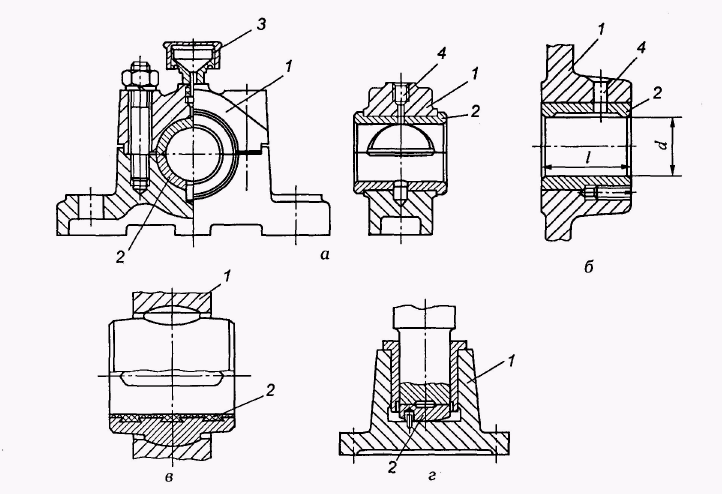
Рис. 12.1. Типи підшипників ковзання: а–в – радіальні; г – упорний;
1 – корпус; 2 – вкладиш; 3 – змащуючий пристрій; 4 – отвір для підведення мастильного матеріалу
Підшипники ковзання складаються, як правило, з корпуса 1 (див. рис. 12.1), вкладишів 2 і змащувальних пристроїв 3.
Основним елементом підшипника є вкладиш.
Оцінка підшипників ковзання
Переваги підшипників ковзання:
висока надійність при змінних і динамічних навантаженнях;
нормальна робота при високих швидкостях обертання;
безшумна робота;
порівняно малі радіальні розміри;
роз’ємні підшипники полегшують монтаж, допускають встановлення на шийці колінчастих (непрямих) валів.
Недоліки підшипників ковзання:
високі вимоги до наявності мастильного матеріалу, великі витрати мастильного матеріалу;
порівняно великі осьові розміри;
значні втрати на тертя, низький ККД.
Матеріали
Матеріали вкладишів повинні мати низький коефіцієнт тертя, високу теплопровідність, достатню зносостійкість і опір заїданню, високий опір крихкому і втомному руйнуванню.
Металеві вкладиші виготовляють з бронз, бабітів, алюмінієвих сплавів і антифрикційних чавунів. Застосовують металокерамічні вкладиші, пористі, насичені парами масла і здатні довго працювати без підведення мастильного матеріалу.
Дані про матеріали наведені в табл. Д15.
Види змащування. Змащення підшипників
Для нормальної роботи важливо створити надійне змащення підшипників.
При нерухомому валу на поверхні цапфи і вкладиша повинна зберігатися плівка мастильного матеріала; робота підшипника у цей момент відбувається в умовах граничного змащення.
Вал, що обертається, втягує мастильний матеріал між цапфою і вкладишем і створює гідродинамічну підйомну силу, вал вспливає у зв’язку зі збільшенням швидкості. Товщина мастильної плівки збільшується, умови змащення покращуються. Робота підшипника в цьому випадку відбувається в режимі напіврідинного змащування.
Граничне і напіврідинне змащування – недосконале змащування.
При подальшому зростанні швидкості шар мастила збільшується і повністю перекриває нерівності поверхонь тертя – виникає рідинне змащування. Тертя в цьому випадку мінімальне, а зношування і заїдання відсутні. Такий вид змащування називають гідродинамічним.
Мастильні матеріали бувають рідкими, пластичними, твердими.
Для підведення мастильного матеріалу до поверхонь ковзання у втулках і вкладишах виконують отвори 4 (див. рис. 12.1), пов’язані з осьовими і кільцевими канавками. Мастильний матеріал може підводитись в підшипник примусово (під тиском), самопливом і за допомогою спеціальних пристроїв.
ККД однієї пари підшипників ковзання 0,96...0,98.
Види руйнувань і критерії працездатності підшипників ковзання
Критерієм працездатності підшипників ковзання є зносостійкість – опір зношуванню і заїданню.
Заїдання виникає при перегріві підшипника: знижується в’язкість мастила; мастильна плівка місцями розривається; виникає металевий контакт; утворюються містки мікрозварювання; вириваються частки матеріалу.
Умовний розрахунок підшипників ковзання
Умовний розрахунок підшипників ковзання проводять за двома показниками: середньому питомому навантаженню між поверхнями, які труться p і добутку pV.
Розрахунок за середнім питомим навантаженням забезпечує зносостійкість:
![]() ,
,
де R
– реакція в опорі; d
– діаметр цапфи; l
– довжина цапфи (див. рис.
12.1, б);
![]() – допустимі питомі навантаження на
поверхні тертя. Розрахунок на
нагрівання і відсутність заїдання.
– допустимі питомі навантаження на
поверхні тертя. Розрахунок на
нагрівання і відсутність заїдання.
![]() ,
,
де V – колова швидкість шийки вала або осі. Застосування підшипників ковзання:
для валів великих діаметрів;
для високошвидкісних валів;
для валів, які працюють в умовах ударів і вібрацій, в агресивних середовищах;
для колінчастих валів;
у побутовій техніці.
Перейдемо до розгляду тестових питань для кращого закріплення теми.
Тема: Підшипники ковзання
1. Вказати одну із основних переваг підшипників ковзання: а) малі втрати на тертя; б) малі габаритні розміри; в) надійна робота при високих швидкостях; г) низька витрата мастила. |
2. Який із матеріалів необхідно використовувати для виготовлення деталі 1:
а)
сталь 45; б)
сталь У10; в)
сталь Ст3; г)
БрО10Ф1.
|
3. Які основні причини виходу з ладу підшипників ковзання: а) розтріскування втулки; б) викришування поверхні кульки; в) заїдання і зношування робочої поверхні втулки; г) стирання поверхні цапфи вала. |
4. До якого типу відноситься зображений підшипник:
а) радіального; б) радіально-упорнгого; в) упорного; г) до самовстановлюваного. |
5. Яке призначення вирізу (кишені) 1 на втулці підшипника (див. рис. до завдання 4): а) для зменшення напружень в матеріалі; б) для зменшення ваги; в) для розподілу мастила по довжині; г) для збору залишкового мастила. |
6. Який матеріал з перерахованих не використовується для виготовлення вкладишів для підшипників ковзання: а) сталь 45; б) брА9Ж4Л; в) брО10Ф1; г) чавун АЧК-1. |
7. Яке змащення називають недосконалим: а) рідинне; б) граничне; в) відсутність змащення; г) гідродинамічне. |
8. Які параметри підшипника використовують при його перевірці на нормальний тепловий стан та відсутність заїдання: а) R, t, d, l ; б) R, d, l, ; в) V, R, d, l ; г) V, R, d, l, . |
9. До якого типу відноситься зображений на рисунку підшипник:
а) радіального; б) радіально-упорного; в) упорного; г) до самовстановлюваного. |
10. Який матеріал використовують для елемента 1 підшипника (див. рис. до питання 9): а) алюміній; б) бабіт; в) чавун; г) латунь. |
11. Яке змащення не залежить від частоти обертання вала: а) граничне; б) гідростатичне; в) гідродинамічне; г) напіврідинне. |
12. Вибрати формулу для перевірки підшипника ковзання на тепловий режим та відсутність заїдання: а)
|
13. Які фактори не відносяться до переваг підшипників ковзання: а) безшумність роботи; б) можливість розборки конструкції; в) робота в агресивному середовищі; г) малі втрати на тертя. |
14. Вказати основну причину заїдання поверхонь підшипників ковзання: а) низька чистота поверхонь, що труться; б) викришування поверхонь; в) підвищення температури і руйнування мастильної плівки; г) розтріскування втулки. |
15. Яке навантаження сприймає зображений підшипник 1:
а) осьове; б) значне осьове і радіальне; в) тільки радіальне; г) будь-яке. |
16. Який матеріал використовують для виготовлення деталі 1 (див. рис. до питання 15): а) брО6Ц6С3; б) сталь 45; в) сталь Ст6; г) сірий чавун. |
17. Навантаження якого напряму сприймає зображений підшипник 1:
а) осьове; б) осьове і радіальне; в) тільки радіальне; г) будь-яке. |
18. Яке призначення деталі 1:
а) зменшення втрат на тертя; б) зменшення ваги конструкції; в) покращення теплообміну; г) покращення підводу мастила. |
19. Як відбувається змащення зображеного підшипника (див. рис. до питання 18): а) безперервно маслянкою; б) періодично маслянкою; в) розбризкуванням із мастильної ванни; г) циркуляцією мастильного матеріалу. |
20. Які параметри визначають при перевірці підшипника на нормальний тепловий режим та відсутність заїдання: а) p; V ; б) t; p; в) Ft; l ; г) p. |
21. Визначити допустиме навантаження з умови розрахунку на зносостійкість, якщо: діаметр цапфи вала 50 мм; довжина втулки 70 мм; матеріал втулки–бронза БрА9Ж4; допустиме питоме навантаження 15 Н/мм²: а) 37,5 кН; б) 52,5 кН; в) 73,5 кН; г) 105 кН. |
22. Визначити необхідну довжину втулки з умови розрахунку підшипника на зносостійкість, якщо: реакція в опорі 14 кН; діаметр цапфи вала 45 мм; матеріал втулки–чавун АЧС-2; допустиме питоме навантаження =6 Н/мм²; лінійна швидкість 0,75 м/с:
а)
414,7 мм; б)
52 мм; в)
158 мм; г)
77,9 мм.
|
23. Визначити допустиме навантаження на підшипник ковзання з умови розрахунку на зносостійкість, якщо: діаметр цапфи вала 120 мм; довжина вкладиша 100 мм; матеріал вкладиша–бронза БрА9Ж3; допустиме питоме навантаження =15 Н/мм²: а) 12 кН; б) 180 кН; в) 1,5 кН; г) 90 кН. |
24. З розрахунку на зносостійкість підібрати матеріал для вкладиша підшипника, якщо: радіальне навантаження підшипник 9,6 кН; розміри шийки вала d=50 мм; ℓ=40 мм: а) бронза БрО6Ц6С6: =5 МПа; V=3 м/с; б) бронза БрО4Ц4С4: =3 МПа; V=5 м/с; в) чавун АЧС-1: =0,05 МПа; V=2 м/с; г) бабіт: =10 МПа; V=30 м/с. |
25. Перевірити зображений підшипник 1 на зносостійкість, якщо: матеріал вкладиша–бронза; допустиме питоме навантаження 3 Н/мм²; реакція в опорі 9 кН; діаметр цапфи вала 60 мм; довжина вкладиша 70 мм:
а)
p
<
|
Розділ 13
ПІДШИПНИКИ КОЧЕННЯ
Мати уяву про переваги, недоліки, області застосування, конструкцію, класифікацію і маркування підшипників кочення.
Знати особливості робочого процесу підшипників кочення, види руйнувань, критерії працездатності.
Мати уяву про можливі схеми встановлення валів на підшипниках кочення, про призначення деталей опор на підшипниках кочення, типи змащення, конструкції ущільнень.
Знати формули, фізичний зміст і позначення коефіцієнтів, які входять у формулу для розрахунку еквівалентного динамічного навантаження і довговічності; уміти ними користуватися.
Підшипники кочення складаються із внутрішніх і зовнішніх кілець, тіл кочення і сепараторів, що відділяють тіла кочення один від одного.
Класифікація підшипників кочення
Підшипники кочення класифікують за формою тіл кочення (кулькові і роликові), за числом рядів тіл кочення (однорядні і дворядні); за напрямом сприйняття навантаження (радіальні, радіально-упорні, упорні); за конструктивними особливостями (з канавками на зовнішньому кільці, з однією або двома захисними шайбами та іншими особливостями).
Оцінка підшипників кочення
Переваги підшипників кочення:
порівняно з підшипниками ковзання в підшипниках кочення тертя значно менше, ККД підшипників вищий;
вища несуча здатність;
простота обслуговування;
мала витрата кольорових металів;
мала витрата мастильних матеріалів;
малі осьові розміри;
висока степінь взаємозамінюваності. Недоліки підшипників кочення:
чутливість до ударів і вібрацій;
великі габаритні розміри в радіальному напрямі;
мала довговічність і надійність при високих швидкостях.
Кулькові підшипники
Кулькові радіальні підшипники (рис. 13.1, а) можуть сприймати значне радіальне навантаження і невелике осьове навантаження в обох напрямах. Вони більш дешевші і тому більше використовуються.
Кулькові радіальні сферичні підшипники (рис. 13.1, б), призначені для сприйняття радіальних навантажень, допускають значні перекоси (до 4°) кілець, застосовуються в конструкції з нежорсткими валами або де неможливо забезпечити необхідну співвісність отворів в корпусах.
Кулькові радіально-упорні підшипники (рис. 13.1, ж) відрізняються більшою вантажопідйомністю, призначені для сприйняття комбінованих радіальних і осьових навантажень тільки одного напряму.
Працювати тільки при радіальному навантаженні вони не можуть, під дією радіальних навантажень через нахил контактних ліній виникають внутрішні осьові сили.
Кулькові упорні підшипники (рис. 13.1 и) сприймають лише осьові навантаження, краще працюють на вертикальних валах.
Роликові підшипники
Роликові радіальні підшипники (рис. 13.1, в) випускають з коротким циліндричним роликом, з довгим циліндричним роликом (рис. 13.1, д, голчастий підшипник). Такі підшипники не сприймають осьові навантаження, допускають роздільний монтаж кілець. Роликові підшипники володіють більшою радіальною вантажопідйомністю, допускають лише осьове зміщення кілець.
Крім перерахованих випускають підшипники з витими циліндричними роликами (рис. 13.1, е).
Роликові радіальні сферичні підшипники (рис. 13.1, г) володіють більшою вантажопідйомністю, ніж кулькові, але вони складніші і дорожчі.
Роликові конічні підшипники (рис. 13.1, з) необхідно регулювати при збиранні. Підшипники цього типу допускають роздільний монтаж зовнішнього кільця, сприймають радіальне і осьове навантаження, володіють великою навантажувальною здатністю.
Упорні підшипники можуть бути і роликовими. Вони володіють великою несучою здатністю, практично не допускають перекосу кілець (рис. 13.1, к).
Роликові підшипники виконують з роликами різної форми. Інколи для зменшення габаритних розмірів доріжки кочення виконують прямо на валу або в корпусі машини, а підшипник виготовляють без внутрішнього кільця. Деякі підшипники виготовляють без сепараторів.
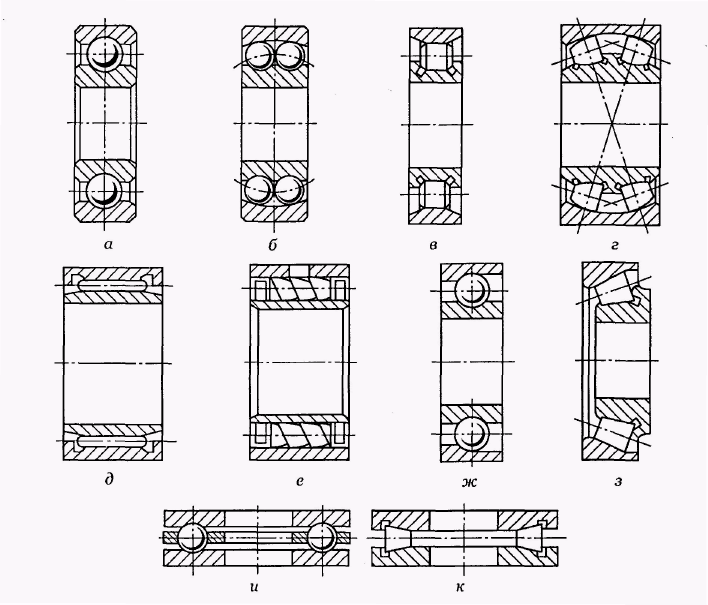
Рис. 13.1. Типи і позначення радіальних (а–е), радіально-упорних
(ж–з) і упорних (и–к) підшипників кочення: а – кульковий радіальний, позначення 0000; б – кульковий радіальний сферичний, позначення 1000; в – роликовий радіальний, позначення 2000; г – роликовий радіальний сферичний, позначення 3000; д – роликовий радіальний голчастий, позначення 4000; е – роликовий радіальний з витим роликом, позначення 5000; ж – кульковий радіально-упорний, позначення 36000, 46000, 66000 в залежності від кута контакту; з – роликовий конічний, позначення 7000; и – кульковий упорний, позначення 8000; к – роликовий упорний, позначення 9000
Серії підшипників
Для одного і того ж діаметра випускають підшипники різних серій (рис.13.2), що відрізняються габаритними розмірами і вантажопідйомністю.
Серії діаметрів і ширини:
особливо легка ... 100;
легка ... 200;
легка широка ... 500;
середня ... 300;
середня широка ... 600;
важка ... 400.
100
200
500
300
600
400
Рис. 13.2. Деякі типорозміри підшипників
Умовні позначення підшипників кочення
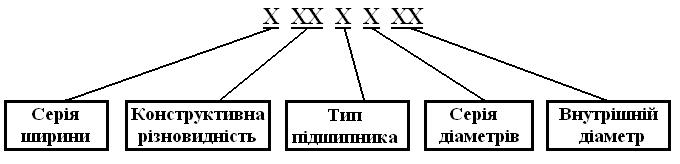
Наприклад: 415 – кульковий радіальний, важка серія, діаметр вала (внутрішній діаметр підшипника) 75 мм; дві останні цифри від 04 до 99 при множенні на 5 дають величину діаметра вала (15x5 = 75 мм);
2206 – роликовий радіальний з коротким циліндричним роликом, легка серія, діаметр вала 30 мм (06 х 5 = 30);
36318 – кульковий радіально-упорний, середня серія, діаметр вала 90 мм (18 х 5 = 90).
Стандарти на деякі підшипники кочення наведені в табл. Д16–Д20.
Види руйнувань і критерії працездатності підшипників кочення
Елементи підшипників (кульки, ролики і доріжки кілець) працюють при циклічно змінному навантаженні. Основними видами руйнувань є втомне викришування робочих поверхонь, зминання робочих поверхонь доріжок, задири та абразивне зношування через попадання пилу і бруду, руйнування сепараторів і кілець.
При порушенні працездатності підшипників з’являється шум.
Основними критеріями працездатності підшипників кочення є довговічність по втомному викришуванню і статична вантажопідйомність для нерухомих підшипників і при частоті обертання n < 1,0 хв-1.
Порядок підбору і перевірка на довговічність підшипників кочення
Підшипники кочення підбирають за каталогом залежно від характера діючого навантаження і діаметра вала. Вибраний підшипник кочення перевіряють на довговічність при динамічній радіальній вантажопідйомності Сr.
Довговічність підшипника – кількість обертів, млн об., яке одне з його кілець робить відносно іншого до початку втомного руйнування матеріалу тіл кочення або кілець.
Базову довговічність визначають при 90 % надійності: зі 100 підшипників можуть бути зруйновані 10:
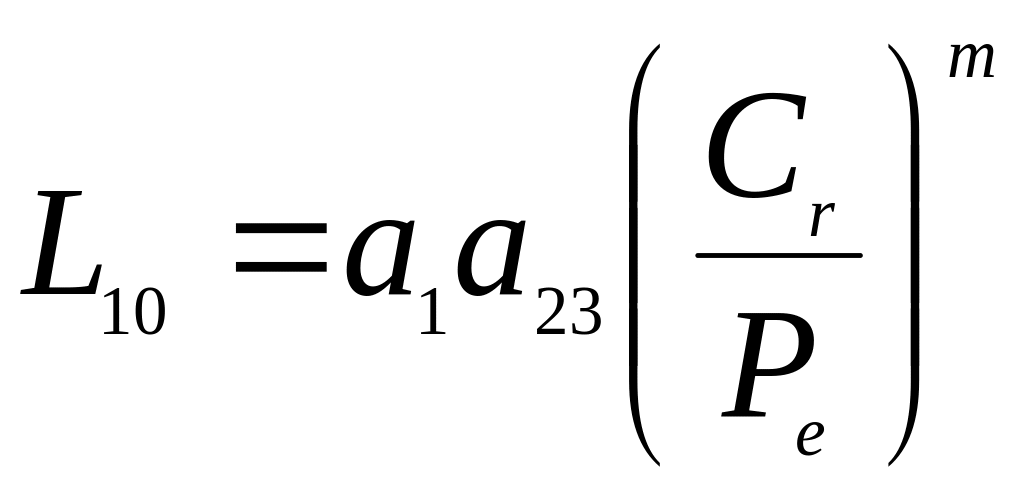 ,
,
де а1 – коефіцієнт довговічності; а23 – коефіцієнт, що враховує вплив властивостей металу кілець і тіл кочення (див. табл. Д21, Д22);
Сr – базова динамічна вантажопідйомність підшипника (визначається за каталогом для вибраного підшипника);
Ре – еквівалентне динамічне навантаження на підшипник;
m – показник степені, m = 3 для кулькових підшипників, m = 10/3 для роликових.
Умова
придатності підшипника:
![]() .
.
Якщо умова не виконана, слід вибрати підшипники наступної серії.
Еквівалентне динамічне навантаження для підшипників:
![]() ,
,
де X,
Y
– коефіцієнти при радіальному й осьовому
навантаженнях, відповідно,
вибираються в залежності від типу
підшипника і співвідношення
осьового
і радіального навантажень
![]() (табл. Д15).
(табл. Д15).
При
відношенні
![]() осьову силу не розраховують (табл. Д23).
осьову силу не розраховують (табл. Д23).
При дії лише радіального навантаження розрахунок ведуть за формулою:
![]() .
.
При
частоті обертання n
![]() 1,0 хв-1
діюче
навантаження розглядають як
статичне і розрахунок ведуть за статичною
вантажопідйомністю:
1,0 хв-1
діюче
навантаження розглядають як
статичне і розрахунок ведуть за статичною
вантажопідйомністю:
![]() ,
,
де Х0, Y0 визначають за каталогом.
Базова динамічна вантажопідйомність – постійне навантаження, яке підшипник може сприймати при базовому ресурсі 1 млн об.
Еквівалентне динамічне навантаження – постійне радіальне навантаження, яке при прикладанні до підшипника з внутрішнім кільцем, що обертається, при нерухомому зовнішньому забезпечить такий же ресурс і надійність, як при дійсному режимі експлуатації.
Деякі конструкції підшипникових вузлів
Фіксуючі опори обмежують осьове переміщення вала в одному або обох напрямах. Плаваючі опори допускають осьове переміщення в обидві сторони (рис. 13.3, 13.4). У плаваючій опорі внутрішнє кільце закріплене з обох сторін, зовнішнє вільне.
Змащування підшипників
Мастильний матеріал оберігає тіла кочення, кільця і сепаратор від безпосереднього контакту і корозії. Вибір мастильного матеріалу залежить від умов роботи підшипника.
Для змащування підшипників кочення, в основному, використовують рідинні мастильні матеріали (очищені мінеральні мастила).

Рис. 13.3. Схема встановлення вала, коли осьове навантаження на вал не передається. Роликові радіальні підшипники осьове навантаження не сприймають: 1 – манжета; 2 – мастиловідбиваючі кільця
Рис. 13.4. Схема осьової фіксації на двох опорах (враспір): 1 – манжета; 2 – мастиловідбиваючі кільця
Для горизонтальних валів в основному використовують змащування розбризкуванням із мастильної ванни. Мастило заливають в корпус нижче рівня центра нижньої кульки (ролика); якщо при розбризкуванні в підшипник потрапляє надто багато мастила, на вал встановлюють мастиловідбиваючі кільця 2 (див. рис. 13.3).
Для швидкохідних підшипників використовують мастильний туман, який подається по трубопроводах і забезпечує відведення теплоти.
Для вертикальних валів використовують змащування підшипників дією відцентрових сил (конусні насадки), на валах використовують крапельне змащування індивідуальними маслянками.
Для
змащування підшипників застосовують
і пластичні
мастила
(рідка основа і загусник), які не
розтікаються. Змащувальний матеріал
повинен займати
![]() вільного об’єму підшипника. Періодичність
заміни мастила залежить від умов роботи.
вільного об’єму підшипника. Періодичність
заміни мастила залежить від умов роботи.
У спеціальних умовах застосовують тверді мастила (порошки графіта, фторопласт і ін.).
Ущільнення (ущільнюючі пристрої) призначені для захисту підшипника від проникання забруднень, вологи і запобігання витікання мастильного матеріалу.
До контактних ущільнень (див. рис. 13.4) відносяться манжети 1, повстяні і металеві кільця. Лабіринтні і щілинні ущільнення мають спеціальні канавки, які інколи заповнюються консистентним мастильним матеріалом. До цієї ж групи можна віднести ущільнення захисними шайбами.
А тепер перейдемо до розгляду тестових питань із цієї теми.
Тема: Підшипники кочення
1. Вказати тип зображеного підшипника:
а) радіальний; б) радіально-упорний; в) радіальний сферичний; г) упорний. |
2. Як при розрахунку радіального підшипника враховується вплив осьового навантаження: а) коефіцієнтом V; б) коефіцієнтом Y; в) коефіцієнтом X; г) коефіцієнтом Kδ. |
3. Який з підшипників зображеного вала сприймає осьове навантаження:
а) лівий підшипник; б) правий підшипник; в) обидва підшипники; г) жоден із вказаних. |
4. Вибрати позначення зображеного підшипника:
а)
105; б)
107; в)
307; г)
1207.
|
5. Як при розрахунку підшипника враховується вплив радіального навантаження: а) коефіцієнтом V; б) коефіцієнтом Y; в) коефіцієнтом X; г) коефіцієнтом Kδ. |
6. Вибрати формулу для визначення довговічності підшипника: а)
|
7. Через яку деталь кріплення підшипника передається осьове зусилля Fa на корпус редуктора:
а) через ліву кришку 1; б) через праву кришку 4; в) через ліву втулку 2; г) через ліве кільце 3. |
8. Як враховується при розрахунку підшипників кочення число робочих змін машини: а) коефіцієнтом V; б) коефіцієнтом Kδ ; в) коефіцієнтом Lh; г) коефіцієнтом Cr. |
9. Вибрати формулу для розрахунку еквівалентного динамічного навантаження для зображеного підшипника, якщо на нього діє радіальна та осьова сила:
а)
|
10. Який підшипник зображеного вала сприймає осьове навантаження:
а) підшипник лівої опори; б) підшипник правої опори; в) обидва підшипника; г) осьове навантаження на підшипник не передається. |
11. Яке навантаження може сприймати зображений підшипник:
а) радіальне; б) радіальне й осьове; в) осьове; г) осьове і радіальне. |
12. Через яку деталь вузла кріплення підшипника передається на корпус вказане осьове зусилля на вал:
а) через деталь 1; б) через деталь 2; в) через деталь 3; г) через деталь 4. |
13. Вказати основні геометричні розміри підшипника №207: а) 45х85х19 мм; б) 35х72х17 мм; в) 35х80х21 мм; г) 45х100х25 мм. |
14. Що характеризує
коефіцієнт а23
у
формулі для розрахунку довговічності
(млн об.) кулькових підшипників
а) довговічність підшипника; б) вплив швидкості обертання; в) надійність роботи; г) якість металу і умови експлуатації. |
15. Як зміниться довговічність підшипника кочення, якщо в підшипнику при роботі буде обертатися не внутрішнє, а зовнішнє кільце:
а) довговічність збільшиться; б) довговічність зменшиться; в) довговічність не зміниться; г) неможливо дати відповідь. |
16. Яке навантаження може сприймати зображений підшипник:
а) осьове; б) радіальне; в) радіальне і невелике осьове; г) значне радіальне й осьове навантаження. |
17. Визначити по стандарту базову динамічну вантажопідйомність зображеного підшипника:
а)
30,7 кН; б)
19,6 кН; в)
52 кН; г)
12,8 кН.
|
18. Розрахувати еквівалентне динамічне навантаження для кулькового радіального підшипника, якщо: Fr=1200Н; Fa=0; навантаження стале: а) 1200 Н; б) 1800 Н; в) 1600 Н; г) 1380 Н. |
19. Розрахувати еквівалентне динамічне навантаження для кулькового підшипника №212, якщо: радіальне навантаження на опорі 860 Н; осьове навантаження 520 Н: X=0,56, Y=1,55: а) 2020,12 Н; б) 657,5 Н; в) 1289,15 Н; г) 1632,34 Н. |
20. Визначити за стандартом базову динамічну вантажопідйомність підшипника №206: а) 1 кН; б) 19,5 кН; в) 14 кН; г) 12 кН. |
21. Розрахувати довговічність в млн об. підшипника №312, якщо: радіальне навантаження 2500 Н; осьове навантаження відсутнє: а) 53266; б) 40800; в) 35158; г) 48300. |
22. Визначити за стандартом базову динамічну вантажопідйомність підшипника №209: а) 44 кН; б) 18,6 кН; в) 33,2 кН; г) 25,5 кН. |
23. Розрахувати довговічність в годинах підшипника 209, якщо: радіальне навантаження 2500 Н, частота обертання вала 1000 хв-1: а) 28600; б) 39033; в) 40000; г) 45300. |
24. Розрахувати еквівалентне динамічне навантаження підшипника №2210, якщо: радіальне навантаження на опорі 1660 Н; осьове навантаження на валу 1200 Н; X=0,74; Y =1,04: а) 1212 Н; б) 2476 Н; в) 3212 Н; г) 5530 Н. |
25. Визначити за стандартом базову динамічну вантажопідйомність підшипника №115: а) 35400 Н; б) 39700 Н; в) 40200 Н; г) 45300 Н. |
Розділ 14
ЗАГАЛЬНІ ВІДОМОСТІ ПРО РЕДУКТОРИ
Мати уяву про типорозміри і виконання, компоновки редукторів.
Знати призначення, основні параметри, переваги і недоліки редукторів основних типів.
Редуктори – це механізми, призначені для пониження кутових швидкостей і збільшення обертових моментів, виконані у вигляді окремих агрегатів. Передача розміщується в окремому жорсткому, закритому корпусі. Редуктори забезпечують стале передавальне число. Передавальні числа стандартних редукторів від 1 до 400, великі передавальні числа застосовують рідко.
При малих передавальних числах застосовують одноступеневі редуктори з передавальними числами до 10, частіше – до 6,37.
Основного поширення отримали двоступеневі редуктори з передавальними числами 15...30.
При великих передавальних числах застосовують триступеневі редуктори; останнім часом вони витісняються компактнішими планетарними.
Частіше застосовують циліндричні зубчасті редуктори.
Схеми редукторів
Найбільш поширені схеми редукторів, зображені на рис. 14.1.
Тип редуктора визначають за виглядом зубчастих передач і порядку їх розміщення в напрямі від двигуна, за числом рівнів і розташуванню геометричних осей тихохідних валів у просторі.
Для позначення типів використаних зубчастих передач застосовують прописні літери: Ц – циліндричні; К – конічні; КЦ – конічно-циліндричні; Ч – черв’ячні; ЧЦ – черв’ячно-циліндричні і таке інше.
На рис. 14.1, а зображено одноступеневий циліндричний редуктор. Такі редуктори випускають з прямозубими, косозубими і шевроними колесами.
Двоступеневі редуктори виконують за розгорнутою (рис. 14.1, б) і співвісною схемами (рис. 14.1, в). Співвісні редуктори зручні, якщо потрібно отримати одну лінію валів з’єднювальних механізмів, мають малі габаритні розміри по довжині, в них досягається однакове змащування коліс із ванни, при цьому збільшуються габаритні розміри вздовж осей валів.

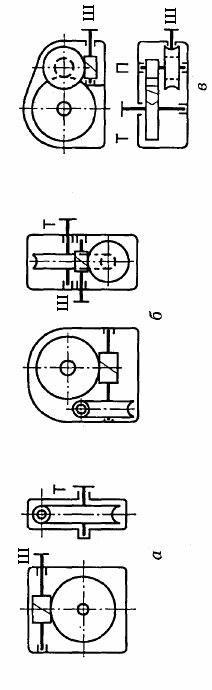
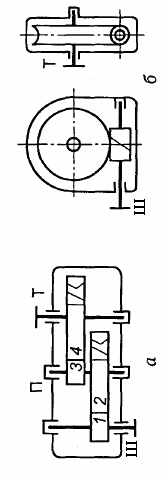

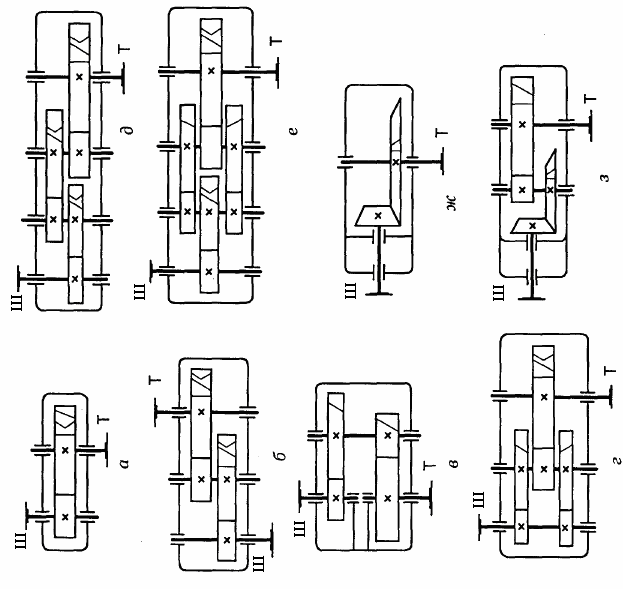
Широкі редуктори позначаються буквою Ш, вузькі – В, співвісні – С.
Для покращення умов роботи тихохідної ступені використовують редуктори з роздвоєною швидкохідною ступенню (рис. 14.1, г), редуктори з роздвоєною ступенню позначаються буквою Ш.
Триступеневі редуктори виконують за розгорнутою (рис. 14.1, д) і роздвоєною (рис. 14.1, е) схемами.
Якщо компоновка машини вимагає взаємної перпендикулярності осей вхідного і вихідного валів, застосовують конічні (рис. 14.1, ж) або конічно-циліндричні (рис. 14.1, з) редуктори.
Великі передавальні відношення, плавність, безшумність і можливість самогальмування забезпечують черв’ячні редуктори (рис. 14.2).
Черв’ячні редуктори випускають з циліндричними, глобоїдними і спіроїдними черв’яками. Велике передавальне відношення при низькому рівні шуму мають двоступеневі черв’ячні і черв’ячно-циліндричні редуктори.
Черв’ячні редуктори випускають з верхнім (рис.14.2, а), нижнім (рис. 14.3, б); боковим або вертикальним розташуванням черв’яка.
Основні недоліки черв’ячних редукторів – низький ККД та малий ресурс роботи.
Осі валів можуть мати різне розташування в просторі. Зазвичай осі валів редукторів розташовані горизонтально в площині роз’єму корпусу редуктора, але використовують також схеми із горизонтальними вхідними (швидкохідними) і вертикальними вихідними (тихохідними) валами.
Основні параметри редукторів
Основними параметрами редукторів є тип, типорозмір і виконання.
Типорозмір
редуктора визначає тип і головний розмір
(параметр) тихохідної ступені. Для
циліндричного і черв’ячного редукторів
головним параметром є міжосьова
відстань aw,
для конічного – зовнішній
ділильний діаметр колеса d2,
для планетарного – радіус водила
R.
Одним з основних параметрів редуктора
є передавальне
число
(табл. Д8).
146
Параметрами редуктора є коефіцієнти ширини коліс, модулі зубчастих коліс, кути нахилу зубців, а для черв’ячного редуктора додатково – коефіцієнт діаметра черв’яка q.
Основна енергетична характеристика редуктора – момент на вихідному валу:
![]() ,
,
де Рвх – потужність на швидкохідному валу; ωвх – кутова швидкість швидкохідного вала; u – передавальне число редуктора; η – ККД редуктора.
Позначення редукторів
У позначенні вказується тип редуктора, число ступеней, схема складання. Якщо вали розташовані в одній горизонтальній площині, в позначенні це не відображається. Якщо всі вали розташовані у вертикальній площині, в позначенні типу додають індекс В, якщо вісь вихідного вала вертикальна – додають літеру Т, якщо вісь швидкохідного вала вертикальна – додають літеру Б.
Цифрами вказуються головний розмір (параметр) тихохідної ступені і передавальне число редуктора.
Наприклад, зображений на рис. 14.3, а редуктор позначається Ц2-200-4: двоступеневий циліндричний редуктор, міжосьова відстань 200 мм, передавальне відношення 4.
Зображений на рис. 14.3, б редуктор позначається Ч-140-25: черв’ячний редуктор, міжосьова відстань 140 мм, передавальне відношення 25.
Опорами валів в редукторах найчастіше є підшипники кочення. Вали циліндричних і конічних редукторів, як правило, встановлюють на кулькових або роликових конічних підшипниках.
При відносно коротких валах осьова фіксація виконується на двох опорах: один підшипник фіксує вал в одному напрямі, а інший – в іншому (на рис. 14.4 тихохідний вал при вказаному напрямі сили Fa2 в осьовому напрямі фіксується на опорі А, встановленій врозпір). Встановлення вала на конічних підшипниках врозпір зображено на рис. 14.5. Таким підшипникам необхідне осьове регулювання зовнішніх кілець, яке виконується за допомогою гвинта 1.
Осьовий зазор в підшипнику може також регулюватися зміною товщини прокладок 1 під кришкою підшипників (див. рис.14.4). Для кріплення коротких валів застосовують встановлення підшипників врозтяг (на рис.14.6 кріплення швидкохідного вала). При напрямі сили Fa, як зображено на рис. 14.6, осьова фіксація відбувається на опорі А. Стакан 2 використовується для регулювання зазору в зачепленні конічних коліс.
Рис. 14.4. Циліндричний одноступеневий редуктор, вертикального виконання: 1– прокладки; А–Г – опори; Fa2 – осьова сила
Рис. 14.5. Циліндричний одноступеневий редуктор з горизонтальним розташуванням валів і їх встановлення на конічних підшипниках врозпір: 1 – гвинт
Рис. 14.6. Конічний редуктор з вертикальним розташуванням тихохідного вала: 1 – пробка; 2 – стакан; 3 – показник рівня; А, Б – опори;
Fa – осьова сила
Рис. 14.7. Черв’ячний редуктор з вертикальним розташуванням черв’яка: А, Б – опори ведучого вала
Довгі вали закріплюють від осьових зміщень в одній опорі, другу опору виконують плаваючою (на рис. 14.4 осьова фіксація швидкохідного вала на опорі В, опора Г – плаваюча; на рис. 14.7 осьова фіксація вала черв’яка на опорі А, опора Б – плаваюча). На плаваючій опорі внутрішнє кільце підшипника кріпиться з обох сторін уступами вала, пружинними кільцями, розпірними втулками.
Зовнішні кільця підшипників кріпляться кришками. Кришки підшипників можуть прикручуватись до корпуса гвинтами (рис. 14.6), під кришки поміщають прокладки. Використовують конструкції з врізними кришками, які поступаються в герметичності (див. рис. 14.4, 14.5).
Змащування редукторів
У редукторах забезпечується змащування зубчастих зачеплень і підшипникових вузлів. Мастило в корпус заливають через отвори в кришках, які закриваються пробками 1.
Рівень мастила контролюється мастиломірною голкою і з допомогою спеціальних вказівників рівня 3. У горизонтальних редукторах тихохідне колесо занурюють в мастило на половину ширини вінця. Іноді використовують спеціальні уловлювачі, які направляють мастило в простір між підшипниками шестірні. У вертикальних редукторах зазвичай достатньо занурення колеса тихохідної ступені.
Ущільнюючі пристрої
Ущільнюючі пристрої оберігають від забруднення ззовні і запобігають витіканню мастильного матеріалу.
Для ущільнення підшипникових вузлів застосовують контактні ущільнення – манжети (див. рис. 14.7, опора Б), щілинні, лабіринтні (див. рис. 14.4, опора Б).
Застосовують також внутрішні ущільнення підшипникових вузлів. При змащуванні пластичним матеріалом підшипниковий вузол прикривають мазеутримаючими кільцями.
Тема: Загальні відомості про редуктори
1. Серед наведених схем вказати схему редуктора Ц2В-125-12,5:
а
б
в
г
а) а; б) б; в) в; г) г. |
2. Визначити кутову швидкість вихідного вала редуктора, якщо швидкість на швидкохідному валу редуктора Ц2В-125-12,5 складає 86 рад/с: а) 1075 рад/с; б) 107,5 рад/с; в) 43 рад/с; г) 6,88 рад/с. |
3. Визначити напрям осьового зусилля на швидкохідному валу та вказати який з підшипників сприймає дане навантаження:
а) підшипник 1; б) підшипник 2; в) підшипник 3; г) підшипник 4. |
4. Пояснити призначення деталі 5 (див. рис. до питання 3): а) передача обертового моменту; б) передача осьового зусилля на корпус редуктора; в) утримання мастила; г) спрощення складання. |
5. Вказати спосіб змащення підшипника 4 редуктора (див. рис. до питання 3): а) мастильний матеріал закладено при складанні; б) занурення в мастильну ванну; в) примусове змащення під тиском; г) розбризкування з мастильної ванни. |
6. Серед наведених схем визначити схему редуктора Ц2С-200-16:
а
б
в
г
а) а; б) б; в) в; г) г. |
7. Визначити кутову швидкість вихідного вала, якщо кутова швидкість на швидкохідному валу редуктора Ц2С-200-16 складає 120 с-1: а) 120 с-1; б) 1920 с-1; в) 60 с-1; г) 7,5 с-1. |
8. Як швидкохідний вал зображеного одноступеневого редуктора з’єднюється з валом електродвигуна:
а) з допомогою муфти; б) з допомогою зубчастої передачі; в) з допомогою пасової передачі; г) з допомогою ланцюгової передачі. |
9. Який підшипник тихохідного вала сприймає осьове навантаження при вказаному напрямі обертання (див рис. до питання 8): а) підшипник 1; б) підшипник 2 і 4; в) підшипник 3; г) підшипник 4. |
10. Яке призначення гвинта 5 (див. рис. до питання 8): а) полегшення розбірки вузла; б) полегшення змащення підшипників; в) регулювання підшипників; г) правильну відповідь не вказано. |
11. Серед наведених схем вказати схему редуктора КТ-160-2,8:
а
б
в
г а) а; б) б; в) в; г) г. |
12. Визначити кутову швидкість на вході в редуктор, якщо кутова швидкість на тихохідному валу редуктора КТ-160-2,8 складає 48 с-1: а) 17,14 с-1; б) 50,8 с-1; в) 57,14 с-1; г) 134,4 с-1. |
13. На якій опорі фіксується вал черв’яка в осьовому напрямі:
а) на опорі А; б) на опорі Б; в) на обох опорах; г) відповісти неможливо: це залежить від напряму обертання вала. |
14. Як змащуються підшипники опори Б (див. рис. до питання 13): а) зануренням в мастильну ванну; б) мастильний матеріал закладений при збірці; в) розбризкуванням із мастильної ванни; г) примусовим змащуванням під тиском. |
15. Поясніть призначення деталі 1 (див. рис. до питання 13): а) передача обертового моменту від двигуна; б) зв’язок з машиною-знаряддям; в) передача осьового зусилля на корпус редуктора; г) ущільнення підшипникового вузла. |
16. Серед наведених схем визначити схему редуктора Ц2Ш-160-10:
а
б
г
в
а) а; б) б; в) в; г) г. |
17. Визначити кутову швидкість на швидкохідному валу, якщо кутова швидкість на тихохідному валу редуктора Ц2Ш-160-10 складає 12 с-1: а) 1,2 с-1; б) 16 с-1; в) 160 с-1; г) 120 с-1. |
18. Який підшипник швидкохідного вала сприймає осьове навантаження при вказаному напрямі обертання вала:
а) підшипник 1; б) підшипник 2; в) підшипник 1 і 2 порівну; г) підшипник 2 і 3. |
19. Як відбувається змащення підшипника опори А тихохідного вала (див. рис. до питання 18): а) зануренням в мастильну ванну; б) розбризкуванням із мастильної ванни; в) крапельним змащуванням; г) мастильний матеріал закладений при складанні. |
20. Яка перевага конічних редукторів: а) значне передаточне число; б) порівняно мала маса і габаритні розміри; в) точна фіксація осьового положення коліс; г) передача обертового моменту між валами з осями, що перетинаються. |
21. Серед наведених схем вказати схему редуктора Ц-160-4:
а
б
в
га
а) а; б) б; в) в; г) г. |
22. Визначити обертовий момент на вході редуктора Ц-160-4, якщо: обертовий момент на тихохідному валу редуктора 560 Нм; ККД підшипників кожного із валів 0,99; ККД циліндричного зачеплення 0,98: а) 46,6 Нм; б) 145,8 Нм; в) 2333 Нм; г) 140 Нм. |
23. Як швидкохідний вал зображеного редуктора з’єднується з валом електродвигуна:
а) з допомогою муфт; б) з допомогою зубчастої передачі; в) з допомогою пасової передачі; г) з допомогою ланцюгової передачі. |
24. Який підшипник швидкохідного вала редуктора (див. рис. до питання 23) сприймає осьову силу при вказаному напрямі обертання: а) на опорі А; б) на опорі Б; в) на опорах А і Б порівну; г) осьова сила з вала на опори не передається. |
25. Вказати основну перевагу черв’ячних редукторів: а) велике передавальне число в одній ступені; б) невисокі вимоги до точності встановлення; в) компактність порівняно з іншими передачами; г) високий ККД. |
Розділ 15
МУФТИ
Знати призначення, конструкції основних типів муфт, оцінку муфт і галузі їх застосування; принцип підбору стандартних і нормалізованих муфт і порядок перевірки на міцність основних елементів.
Основні функції муфт – з’єднання валів і передача обертового моменту. З’єднюючи вали машин, муфти виконують і ряд додаткових функцій: компенсують перекоси і зміщення валів, пом’якшують коливання і динамічні навантаження, забезпечують при необхідності плавні пуски і зупинки, запобігають деталі машин від перевантажень і зміни напряму обертання.
Класифікація муфт
Муфти поділяються:
на сталі (глухі, компенсуючі, пружні);
на зчіпні керовані;
на самокеровані (автоматичні) за моментом (запобіжні), за напрямом руху (обгінні), за швидкістю (відцентрові).
Характеристика муфт
1. Жорсткі некомпенсуючі (глухі) муфти не допускають з’єднання валів із зміщеннями або перекосами.
Втулкові муфти (рис. 15.1, а) вимагають співвісності валів. Муфти виготовляють зі штифтами і шпонковим пазом. Муфти прості у виготовленні, дешевші, але встановлення (монтаж) пов’язане з необхідністю великих осьових переміщень валів. Муфти не дозволяють посадки деталей з натягом, не забезпечують жорсткість валів. Фланцеві муфти (рис. 15.1, б) найбільш поширені, в них необхідно забезпечити перпендикулярність торцевих поверхонь до осі валу.
2. Жорсткі компенсуючі муфти допускають з’єднання валів з незначним зміщенням осей. Особливу групу складають шарнірні муфти, які допускають значні перекоси осей валів. Широко поширена зубчаста муфта (мал. 15.1, в). Зовнішня поверхня зубців втулок муфти сферична, зубці мають евольвентний профіль. Внаслідок великого числа зубців муфти мають більшу несучу здатність і надійність. Муфти допускають зміщення валів в осьовому напрямі до 8 мм, в радіальному – до 0,6 мм, перекос – до 1°30’. Зубчасті муфти використовують в широкому діапазоні моментів і швидкостей обертання, вони технологічні і малогабаритні. Основні недоліки – ковзання зубців і їхнє зношування; використовується змащення зубців.
3. Пружні компенсуючі муфти пом’якшують поштовхи й удари, які передаються через вали, що з’єднюються, запобігають від коливань і компенсують всі види перекосів валів. Муфти містять неметалеві пружні елементи (з гуми) або металеві – пружини, пакети пластин.
Пружня втулко-палъцева муфта (МПВП) (рис. 15.1, г) складається із двох напівмуфт, з’єднаних через палець з надітими на нього гумовими втулками. Муфта проста за конструкцією, компактна і мала за масою, гумові кільця, які зношуються, легко замінюються. Муфти допускають осьові зміщення до 5 мм, радіальні зміщення – до 0,6 мм, перекоси – до 1°.
4. Зчіпні керовані муфти служать для з’єднання і роз’єднання валів, що обертаються та не обертаються. Муфти поділяються на муфти з профільним замиканням (кулачкові і зубчасті) і фрикційні. Муфти з профільним замиканням застосовують для передачі значних обертових моментів, якщо не потрібна плавність з’єднання.
Для плавного з’єднання і роз’єднання валів використовують фрикційні муфти (рис. 15.1, д–ж). Робота фрикційних муфт базується на створенні сил тертя між елементами муфти. Силу тертя можна регулювати, змінюючи силу стиску поверхонь, які труться. Керування муфтою може бути механічним, гідравлічним і электромагнітним. За формою поверхонь, які труться, муфти поділяються на дискові, конусні, і циліндричні. Розрізняють сухі та мокрі муфти (працюють з мастилом).
У процесі включення фрикційної муфти відбувається проковзування, і розгін веденого валу іде плавно. Муфта регулюється на передачу максимального моменту, безпечного для елементів машини.
Для зменшення габаритних розмірів муфту виконують із декількома поверхнями тертя – багатодискова муфта (див. рис. 15.1, д). Всі диски муфти мають бути паралельними, плоскими і співвісними, тому всі диски встановлюють на одній з напівмуфт – необхідна абсолютна співвісність валів.
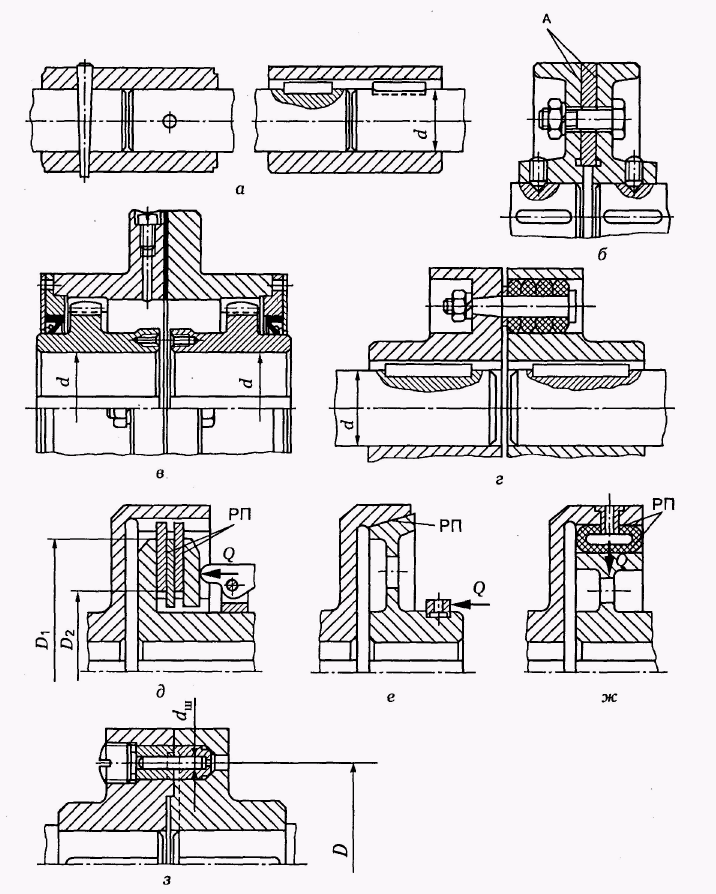
Рис. 15.1. Основні типи муфт: а – втулкова; б – фланцева; в – зубчаста;
г – пружня втулко-пальцева; д – багатодискова; е – конусна; ж – циліндрична шино-пневматична; з – фланцева із зрізаним штифтом;
А – торцьові поверхні; РП – робочі поверхні; Q – керуюче зусилля
Перевагами конусних муфт (див. рис. 15.1, е) є малі сили включення, добра розчеплюваність і простота конструкції. Основні недоліки – великі габаритні розміри і незрівноважені осьові сили, які передаються на вали.
У циліндричній шино-пневматичній муфті (див. рис. 15.1, ж) осьові зусилля на вал не передаються, допускаються осьові зміщення, момент легко регулюється.
Основні недоліки таких муфт – значна вартість гумового балона і нестійкість гуми до нафтопродуктів.
5. Зчіпні самокеровані муфти призначені для зчеплення і розчеплення валів при зміні заданого режиму роботи.
Для цього застосовують обгінні муфти (вільного ходу), які передають момент в одному напрямі, відцентрові муфти для з’єднання і роз’єднання валів при досягненні певної частоти обертання і запобіжні муфти, що виключають механізм при перевантаженнях.
За принципом роботи запобіжні муфти ділять на пружинні, фрикційні та з елементом, який руйнується. За конструкцією пружинно-кулачкові і фрикційні подібні до зчіпних керованих муфт.
Із муфт, з елементом, який руйнується, широко поширена фланцева муфта із зрізаним штифтом (рис. 15.1, з). При перевантаженні штифт зрізається і напівмуфти роз’єднуються. Такі муфти прості за конструкцією, мають малі розміри, основний недолік: для заміни перерізаного штифта необхідно зупиняти машину і замінити штифт.
6. Ланцюгові муфти (рис. 15.2) складається із двох зірочок (з однаковим числом зубців) і охоплюючого їх ланцюга і кожуха.

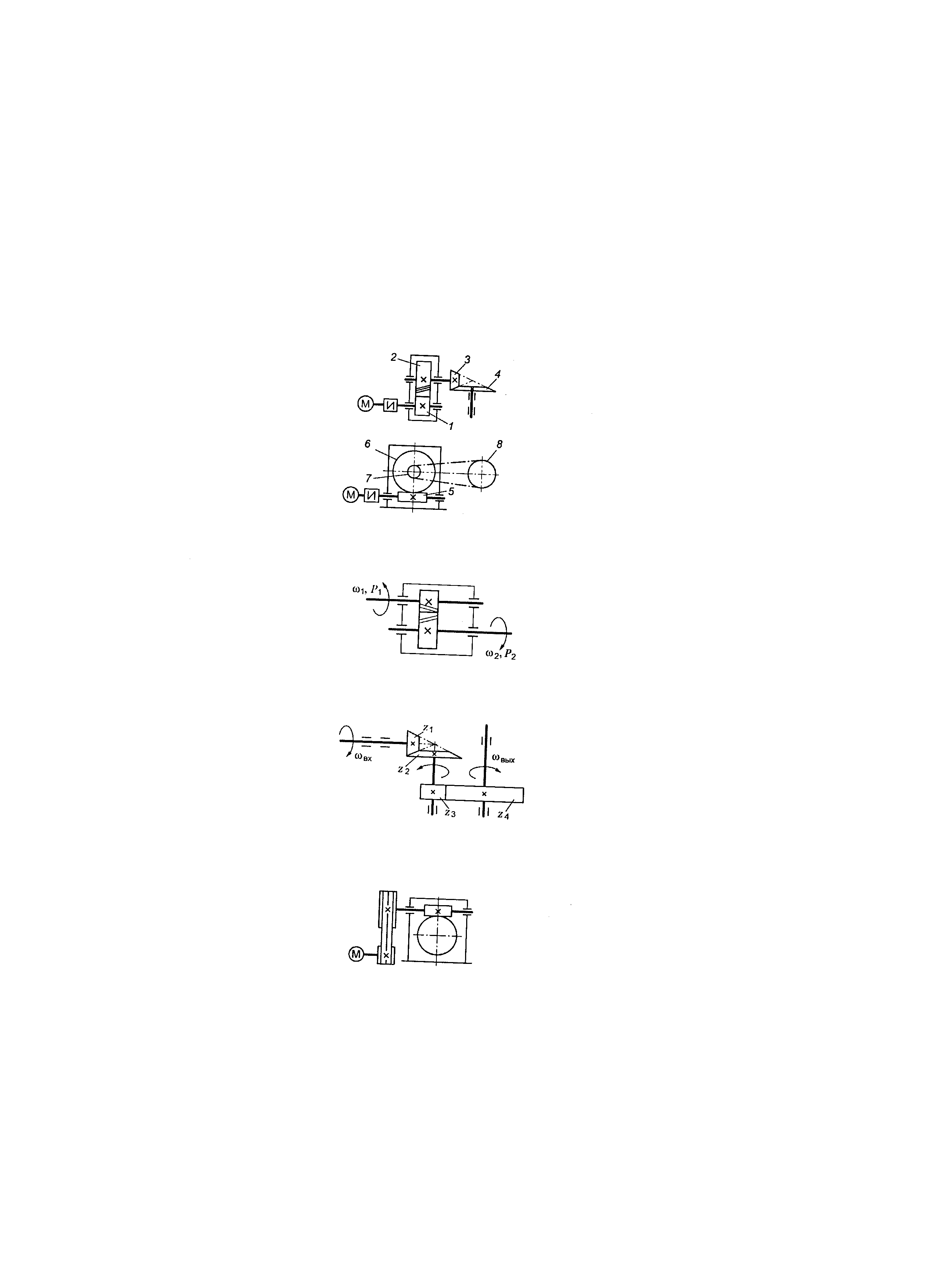
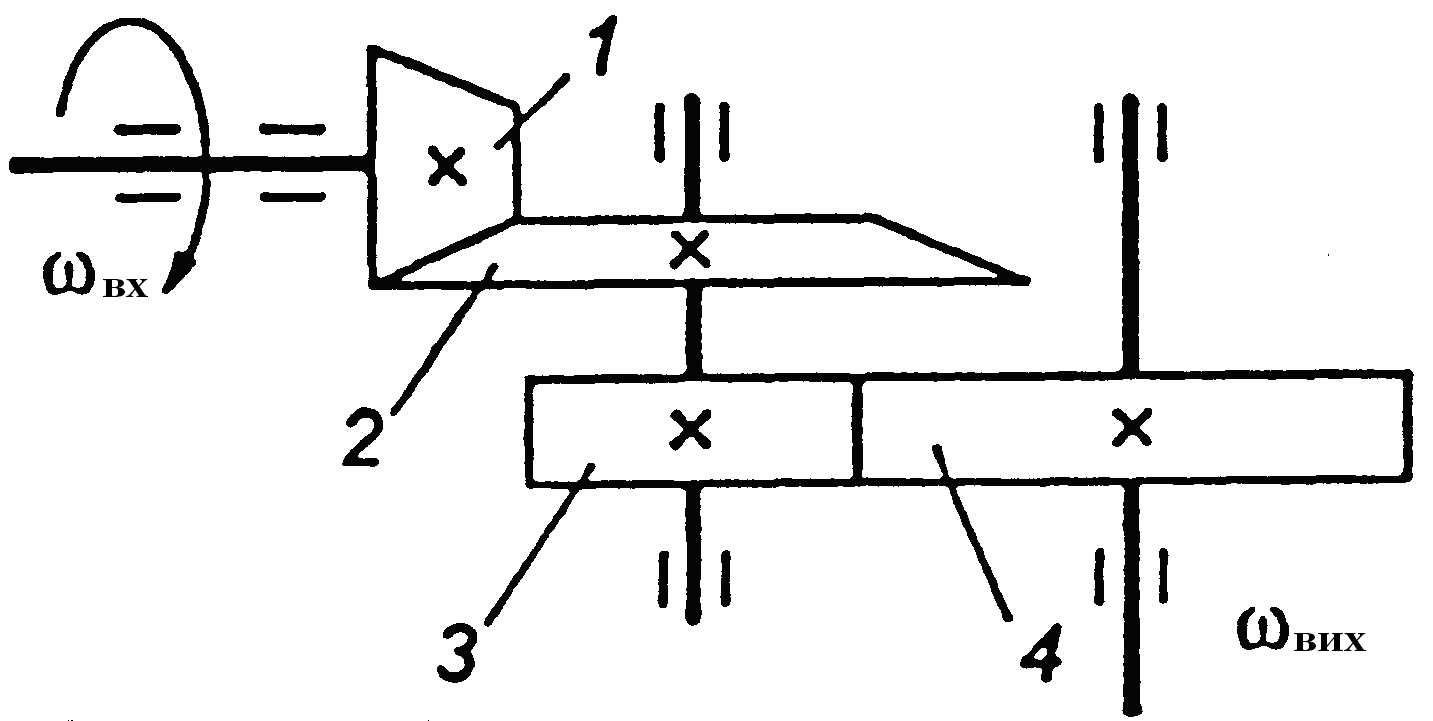
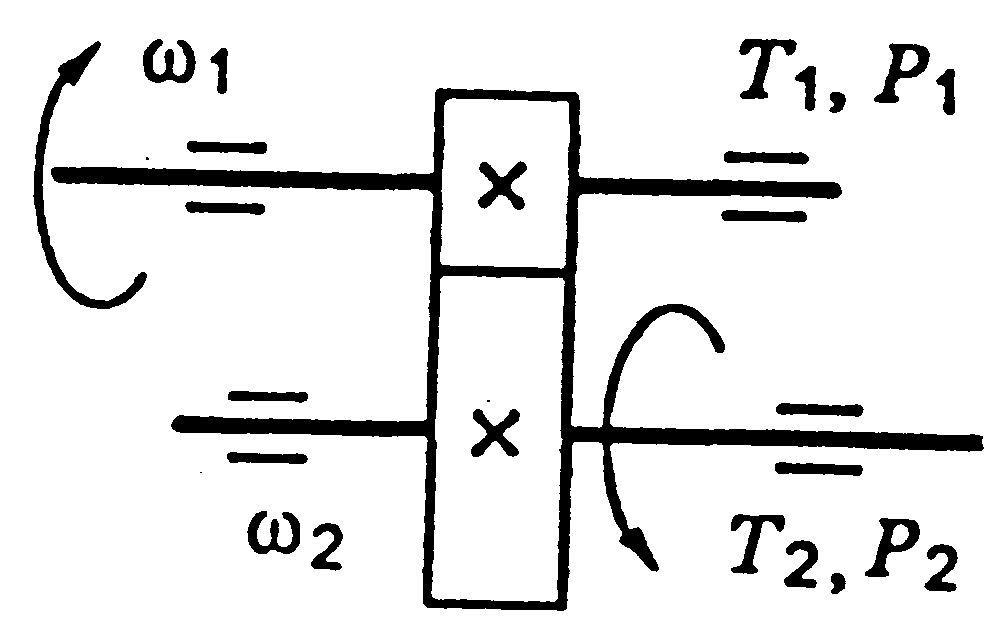
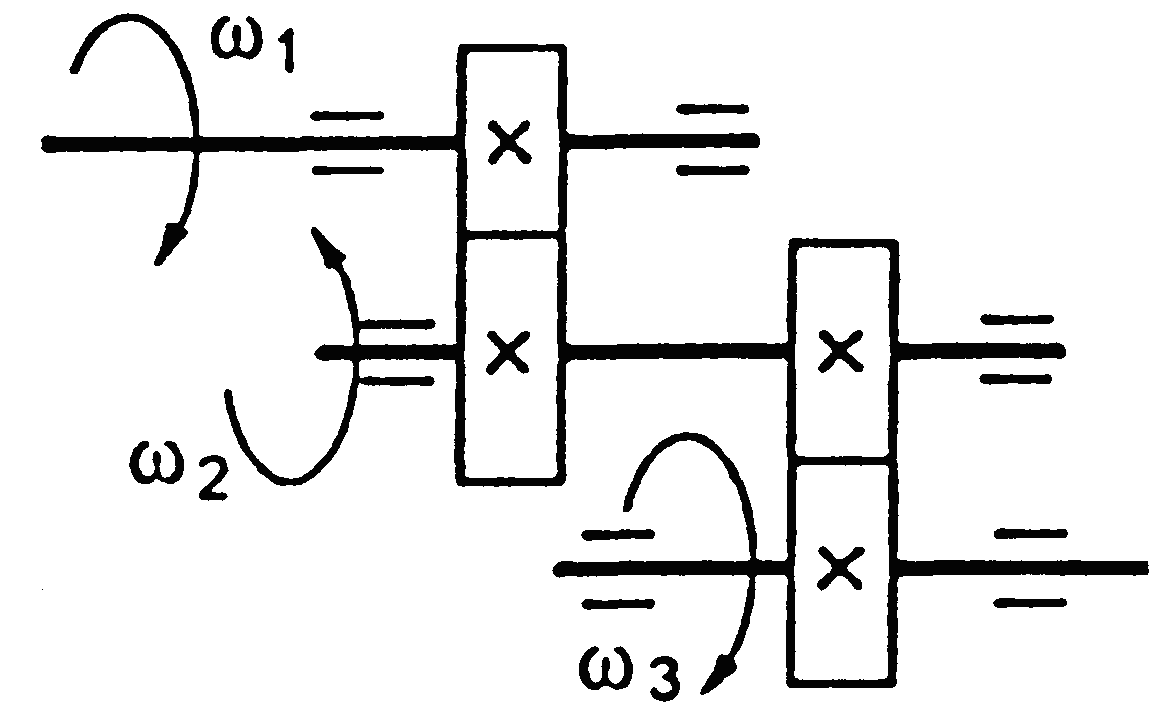
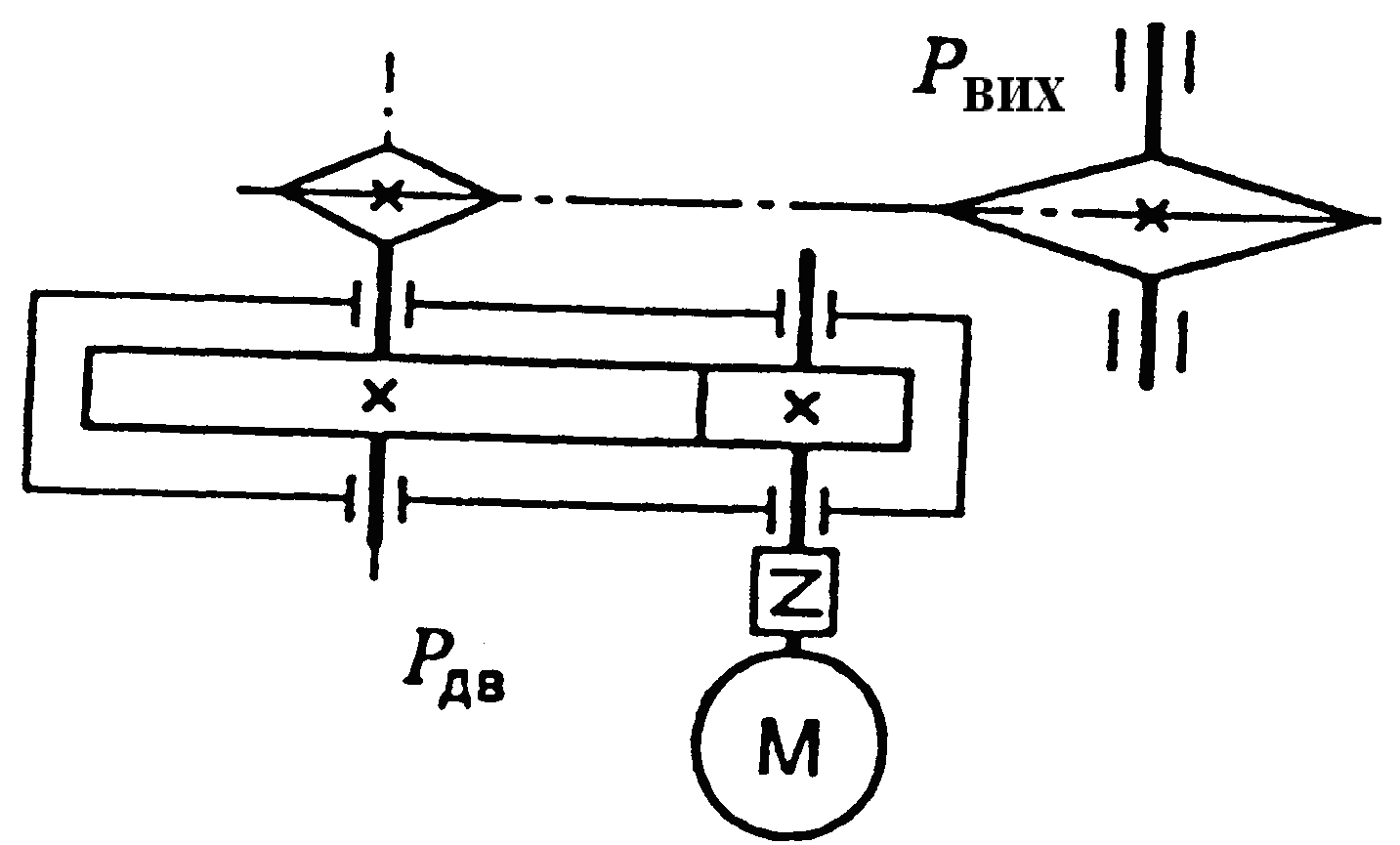
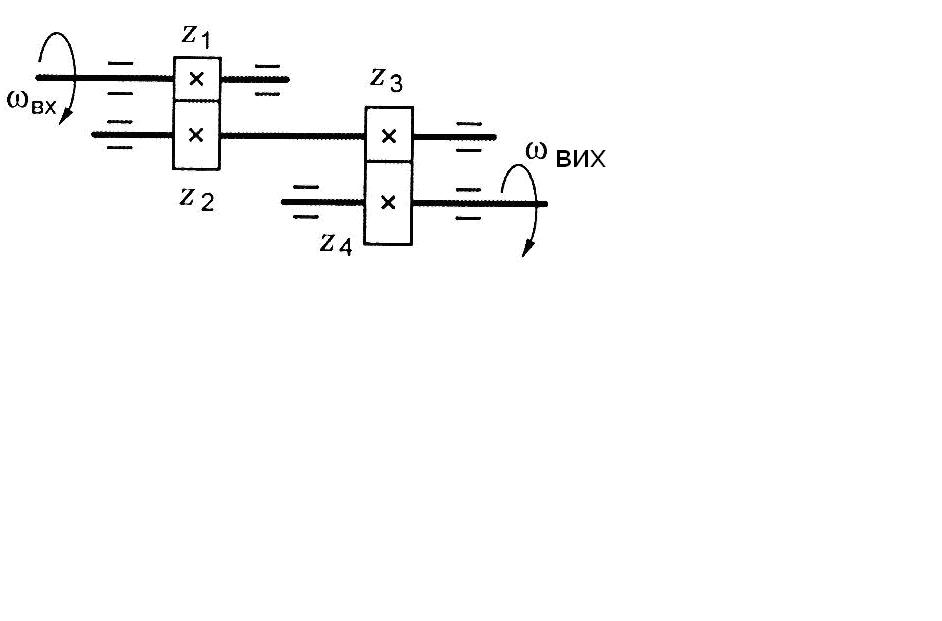
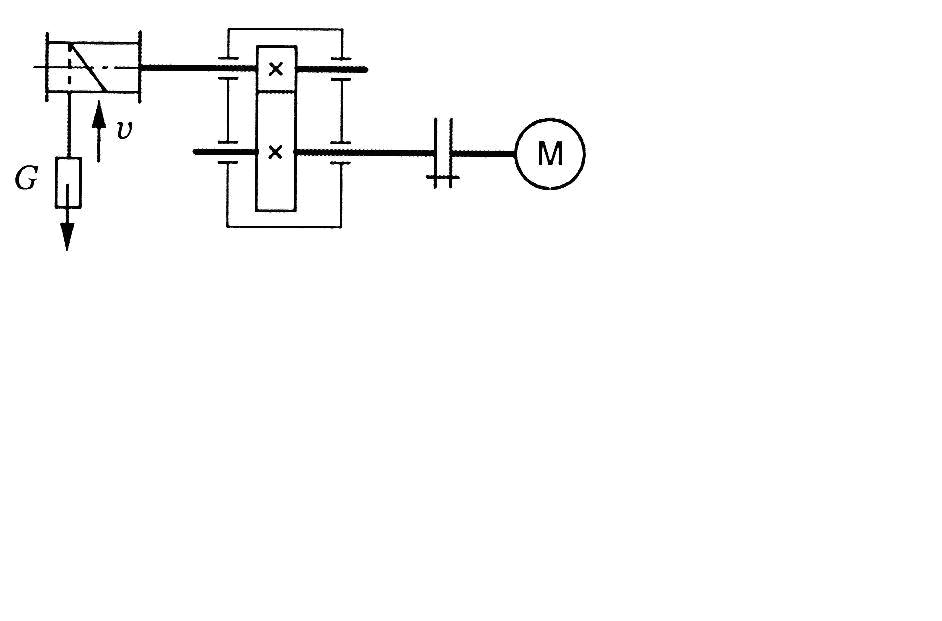
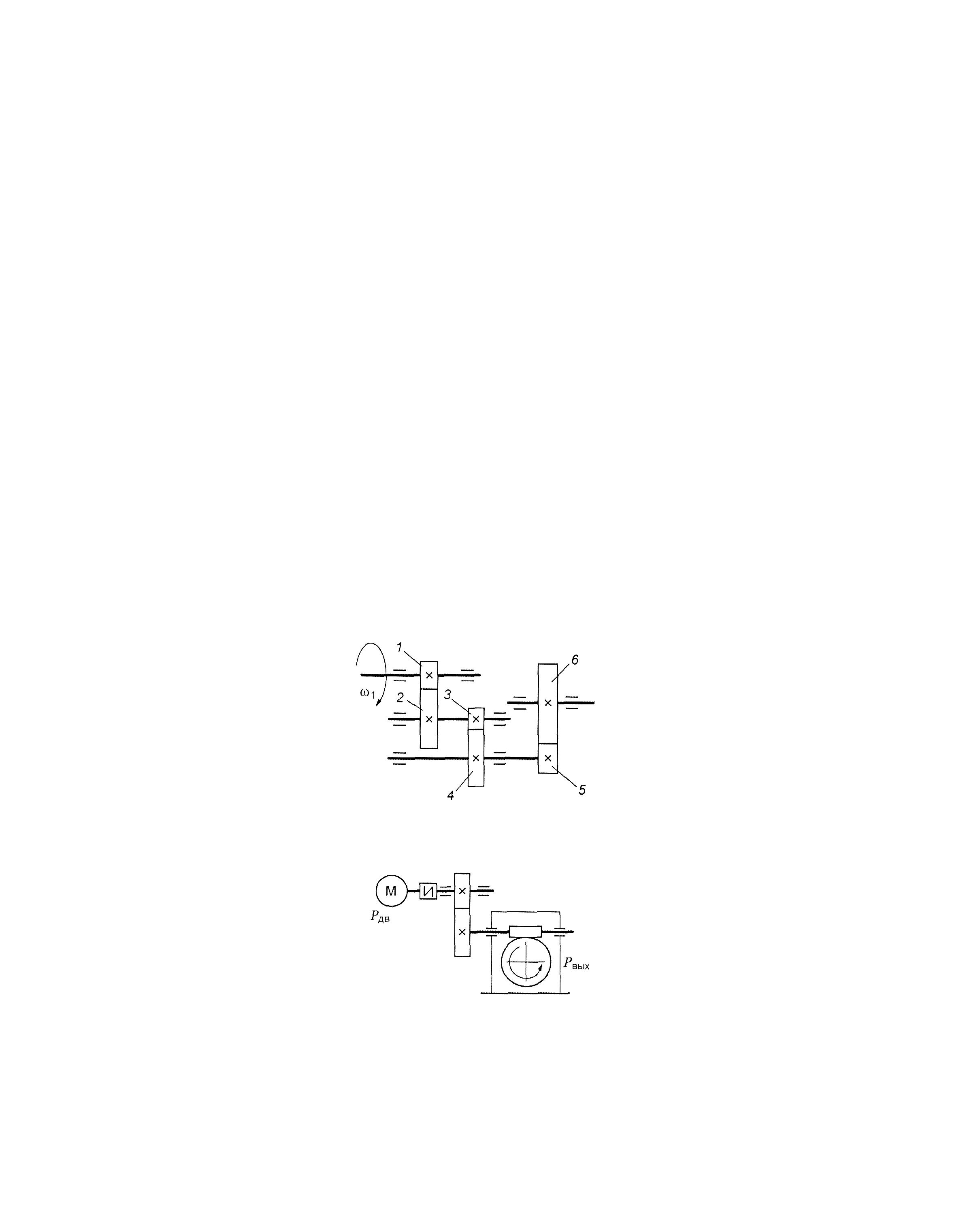
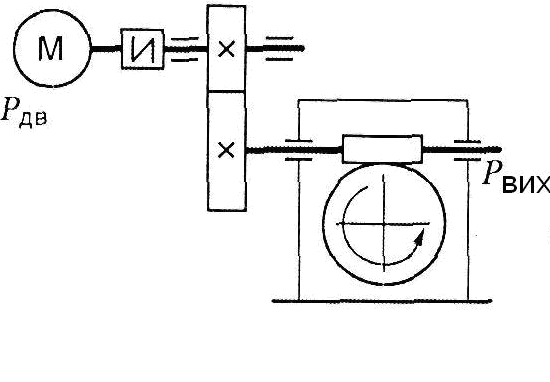
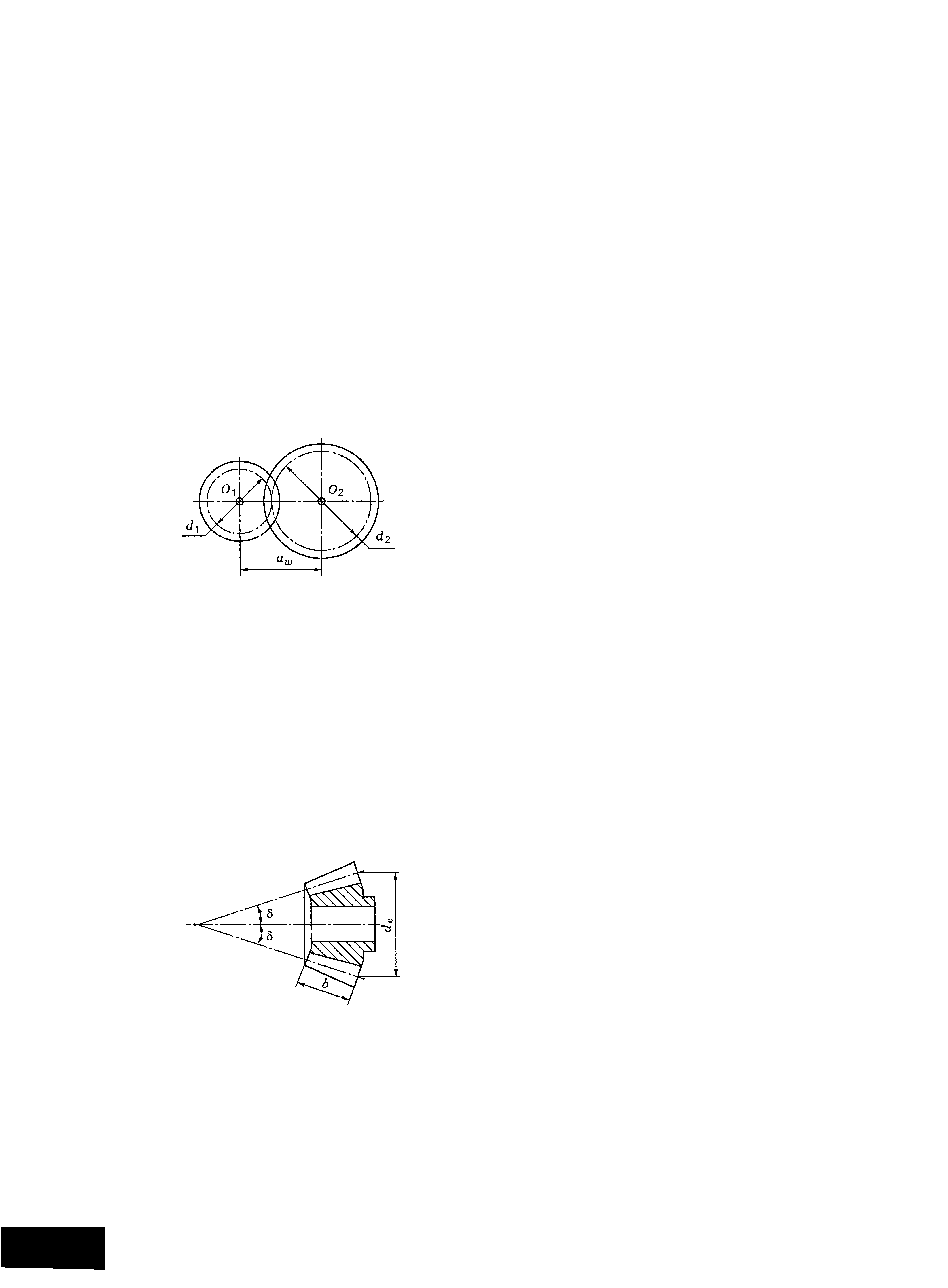
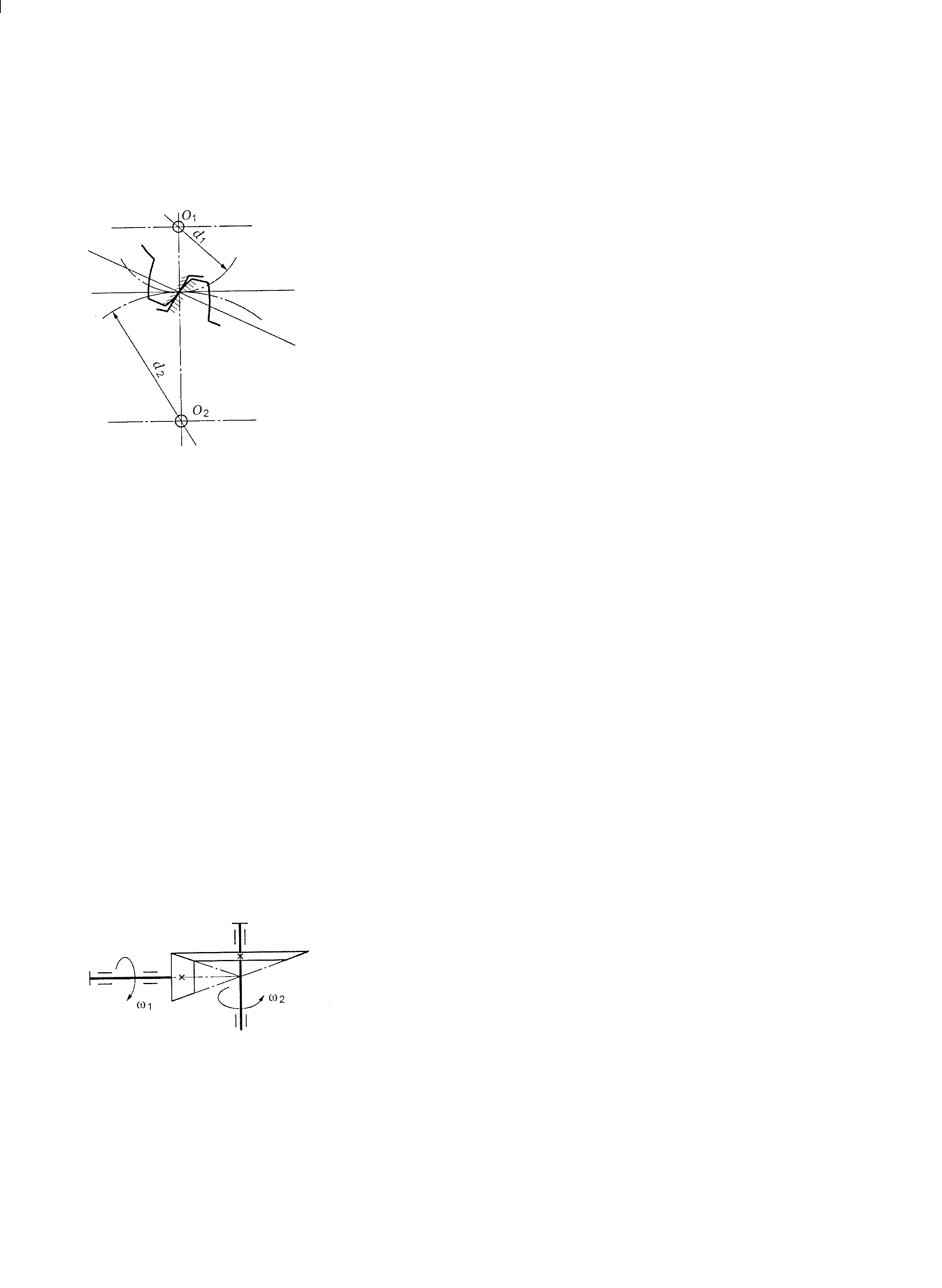
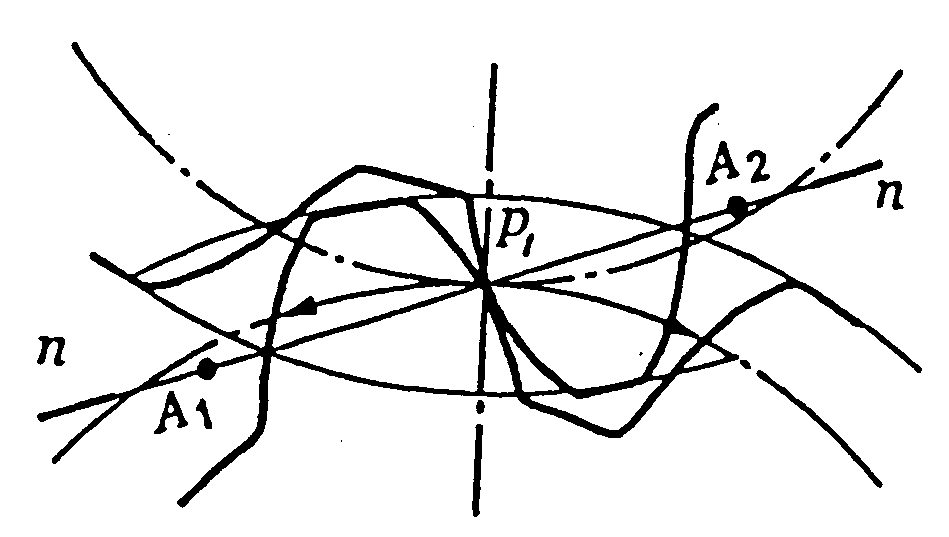
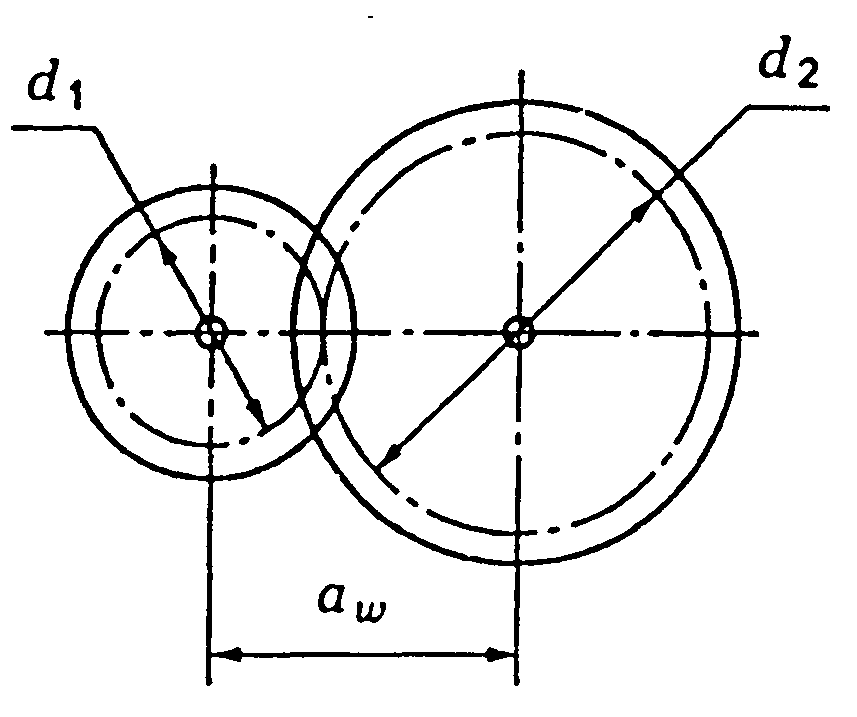
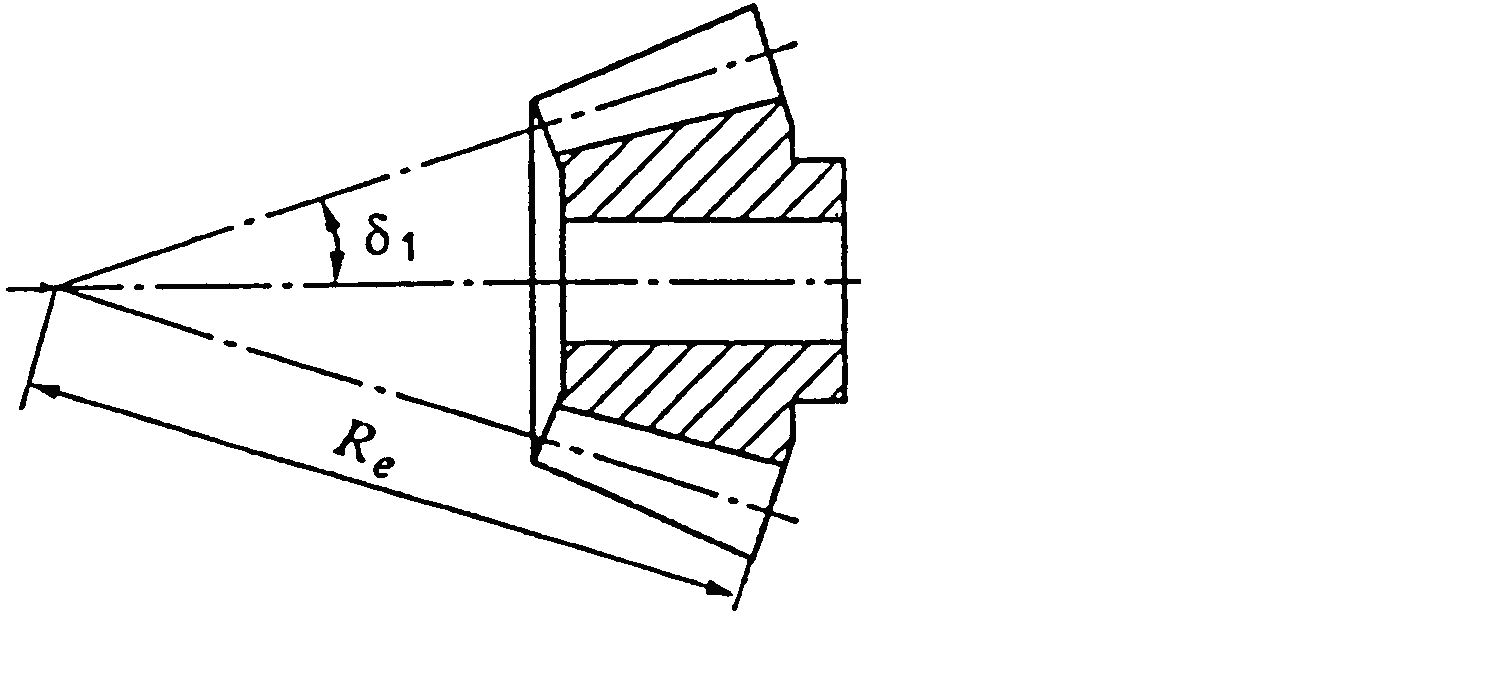

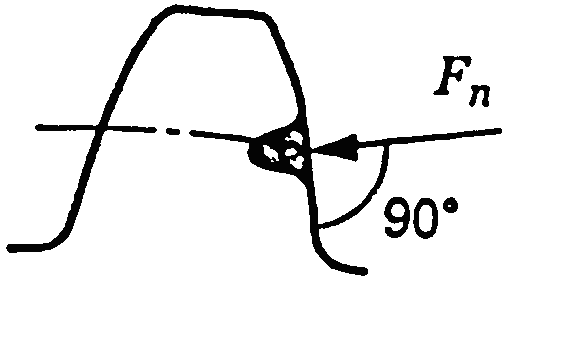
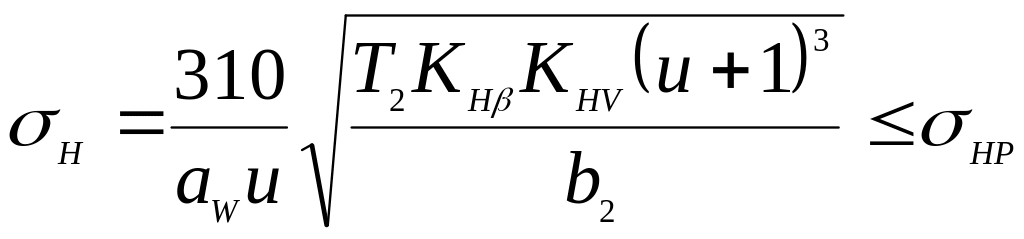 ;
б)
;
б)
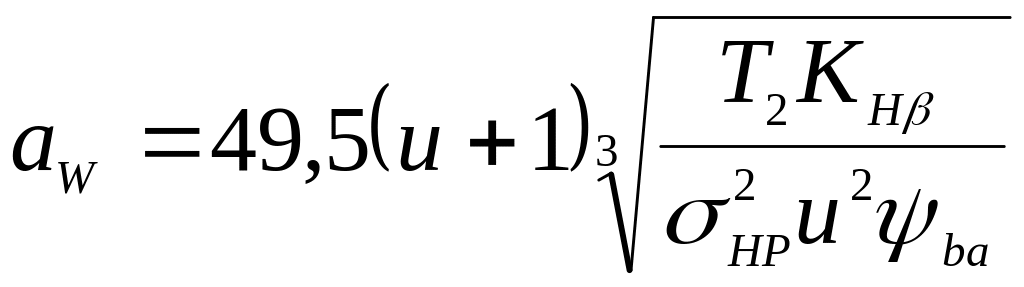 ;
;
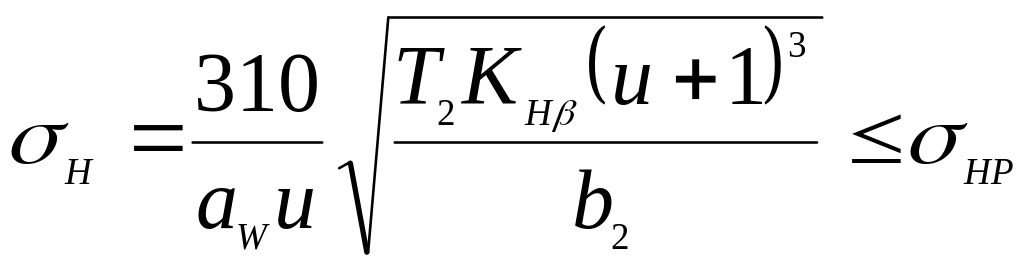 ;
б)
;
б)
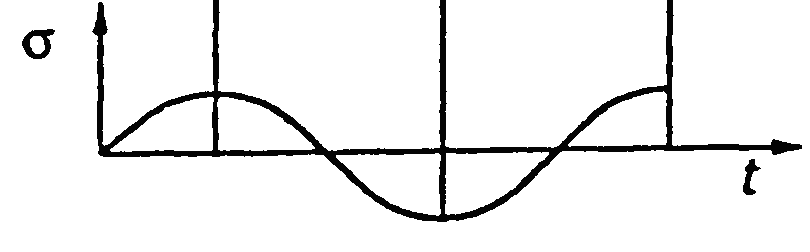
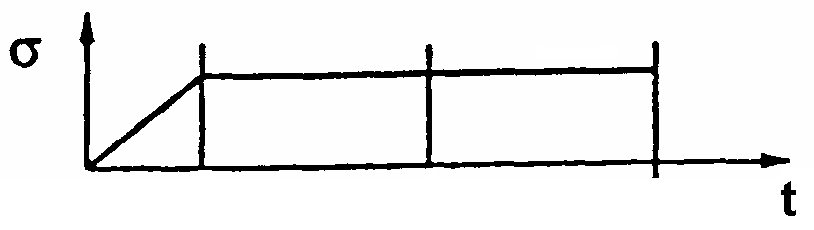
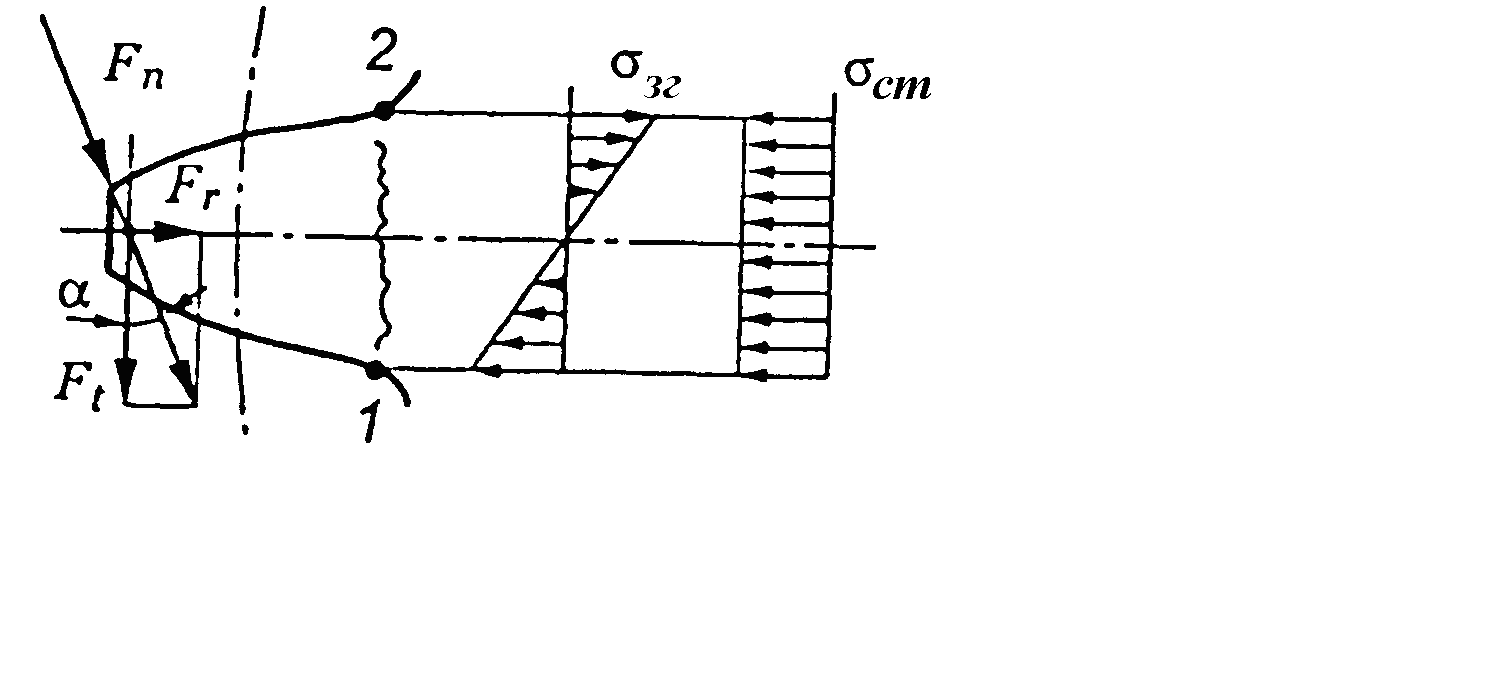
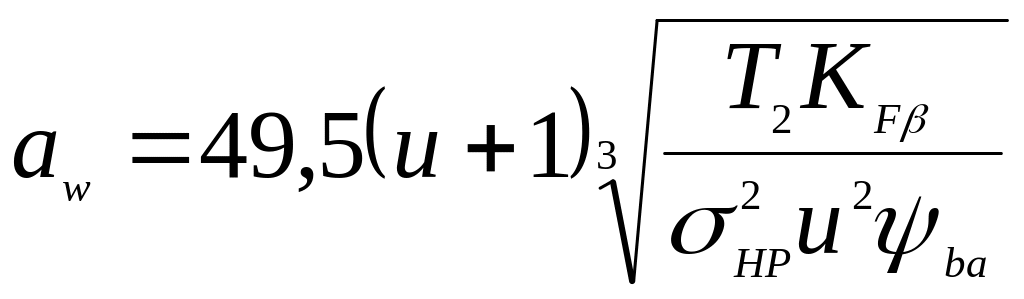 :
:
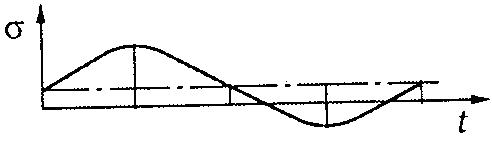
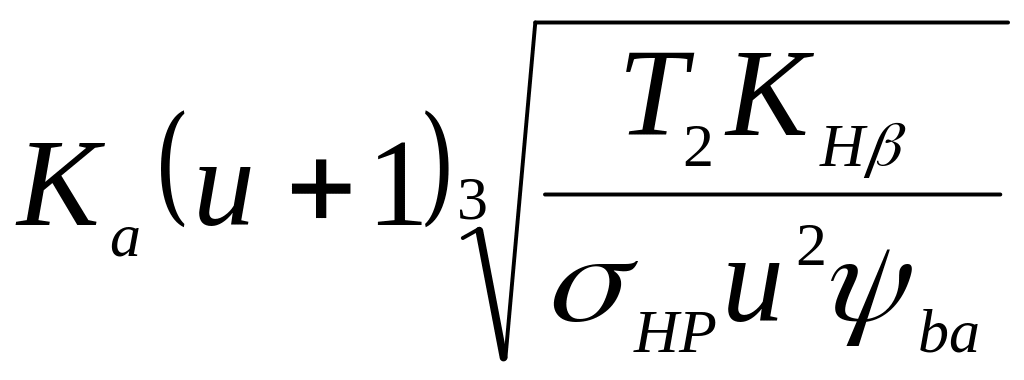 ;
б)
;
б) ;
в)
1; г)
;
в)
1; г)

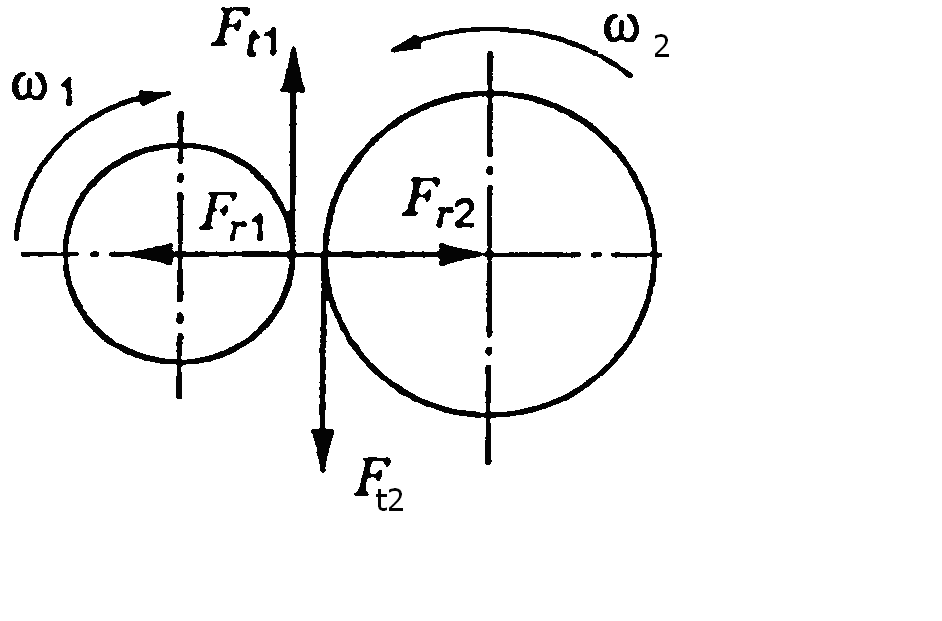
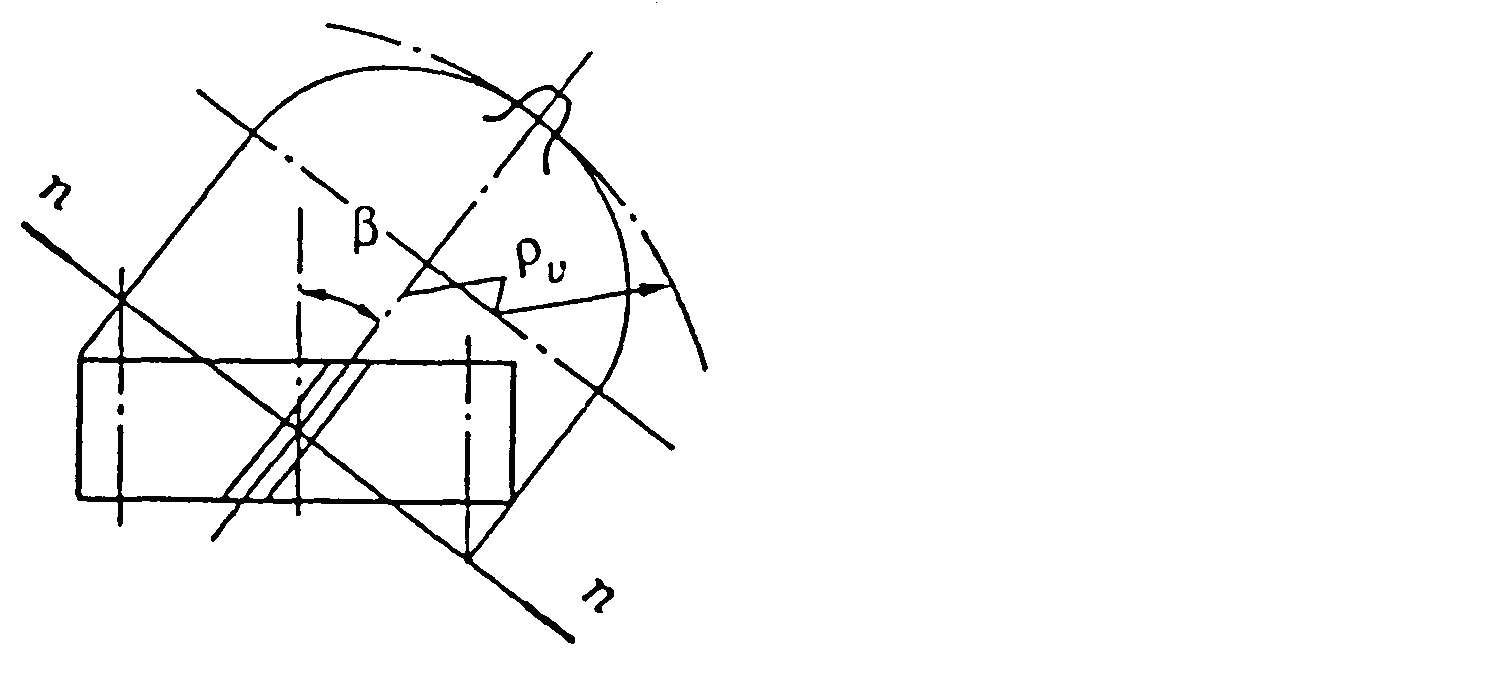
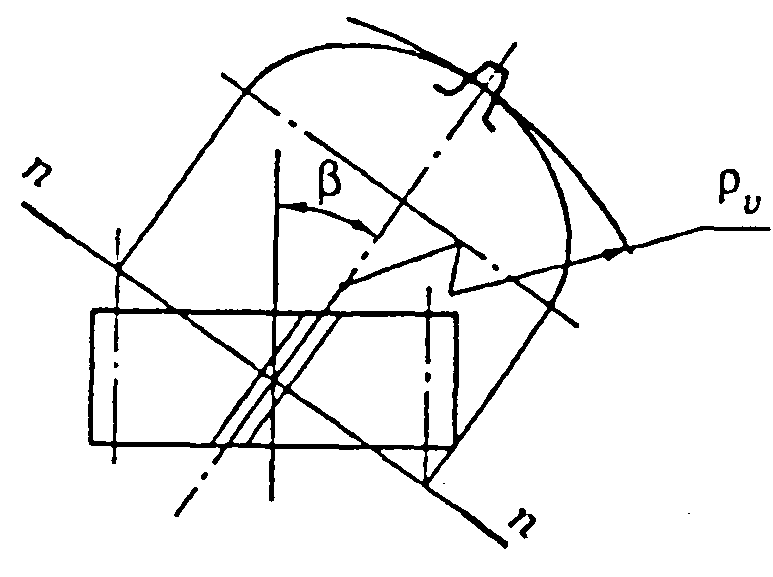
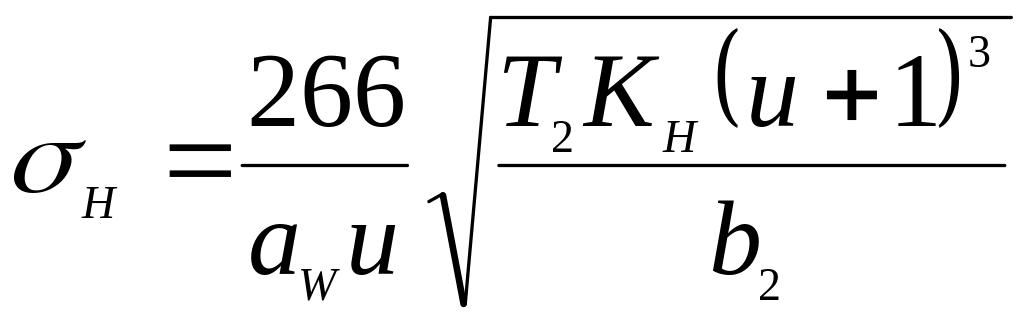 ;
;
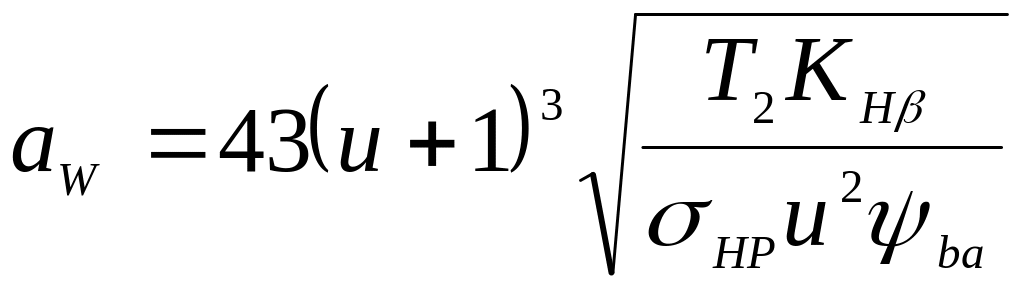 ;
г)
;
г)
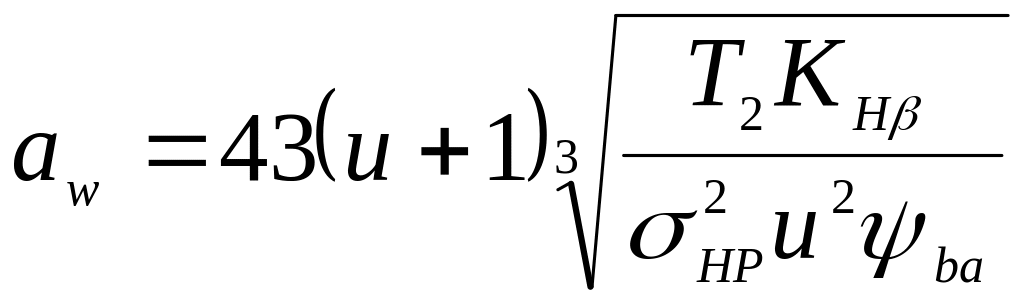
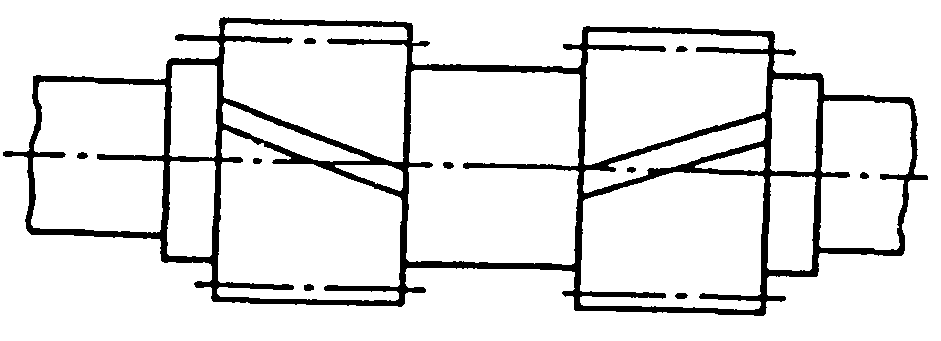
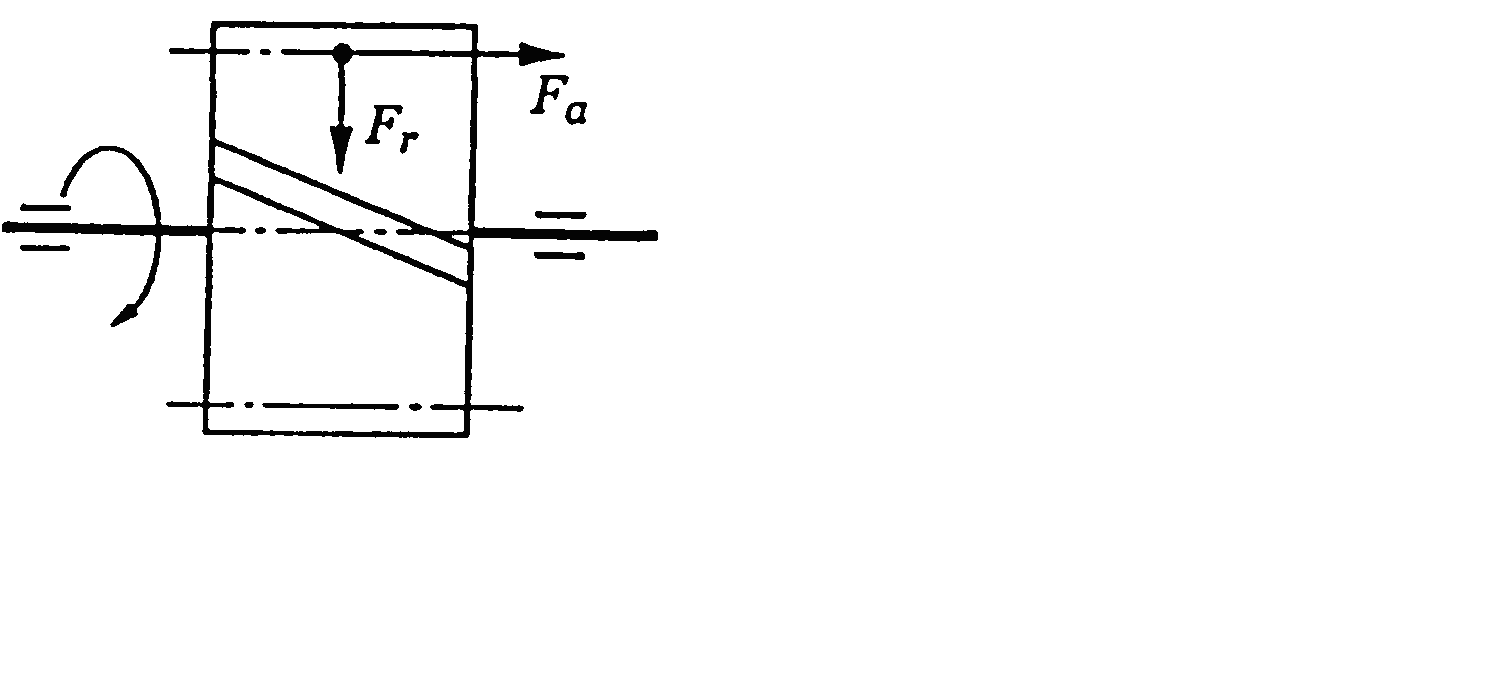
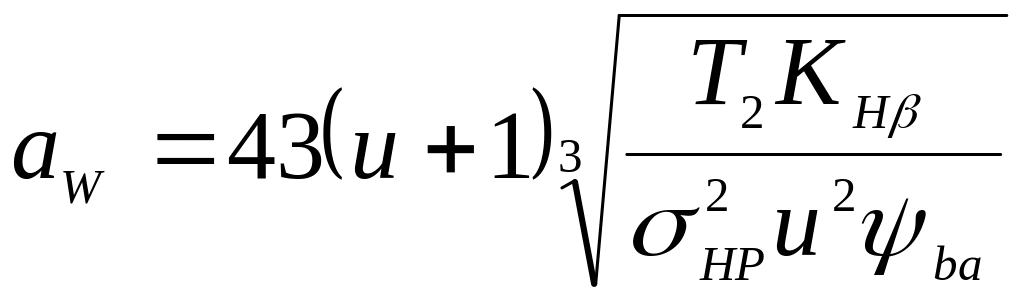 ;
;
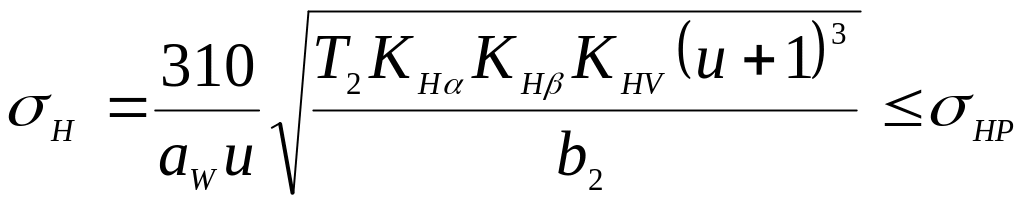 ;
; .
.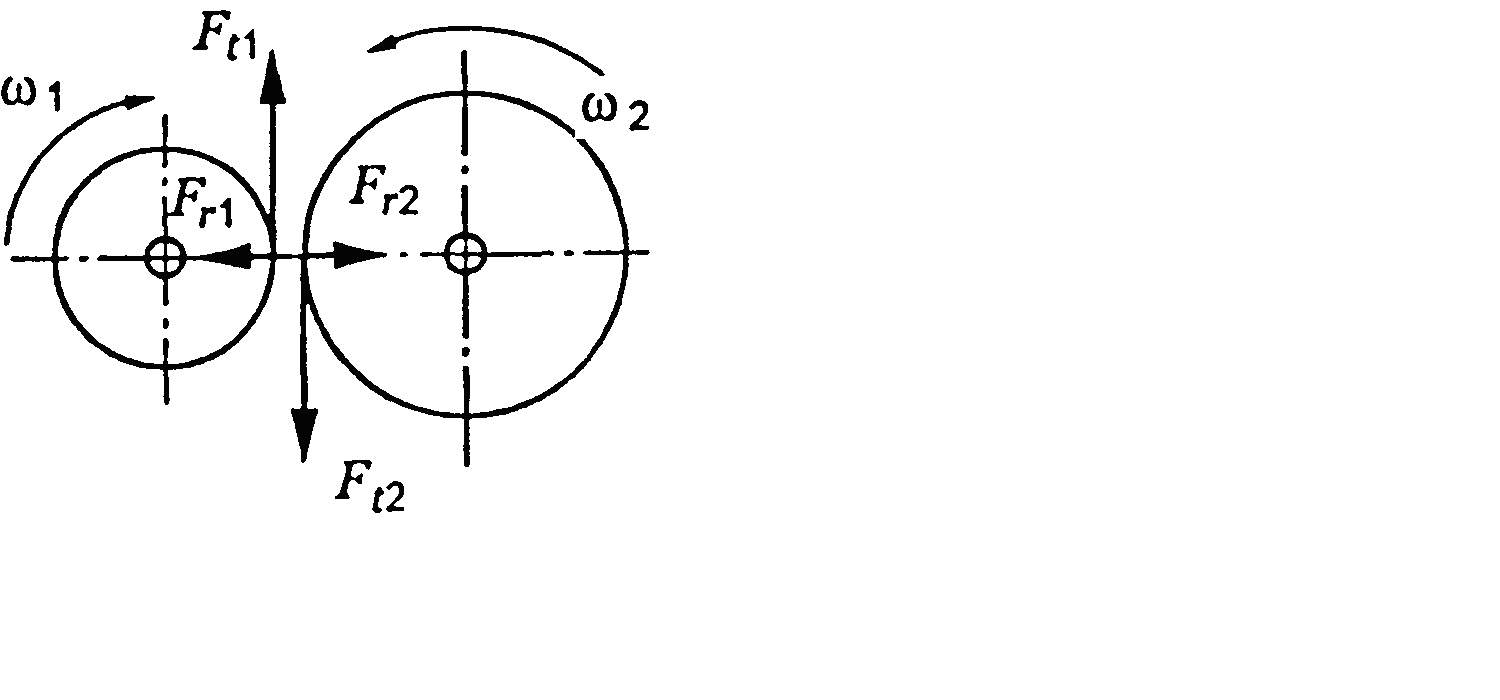
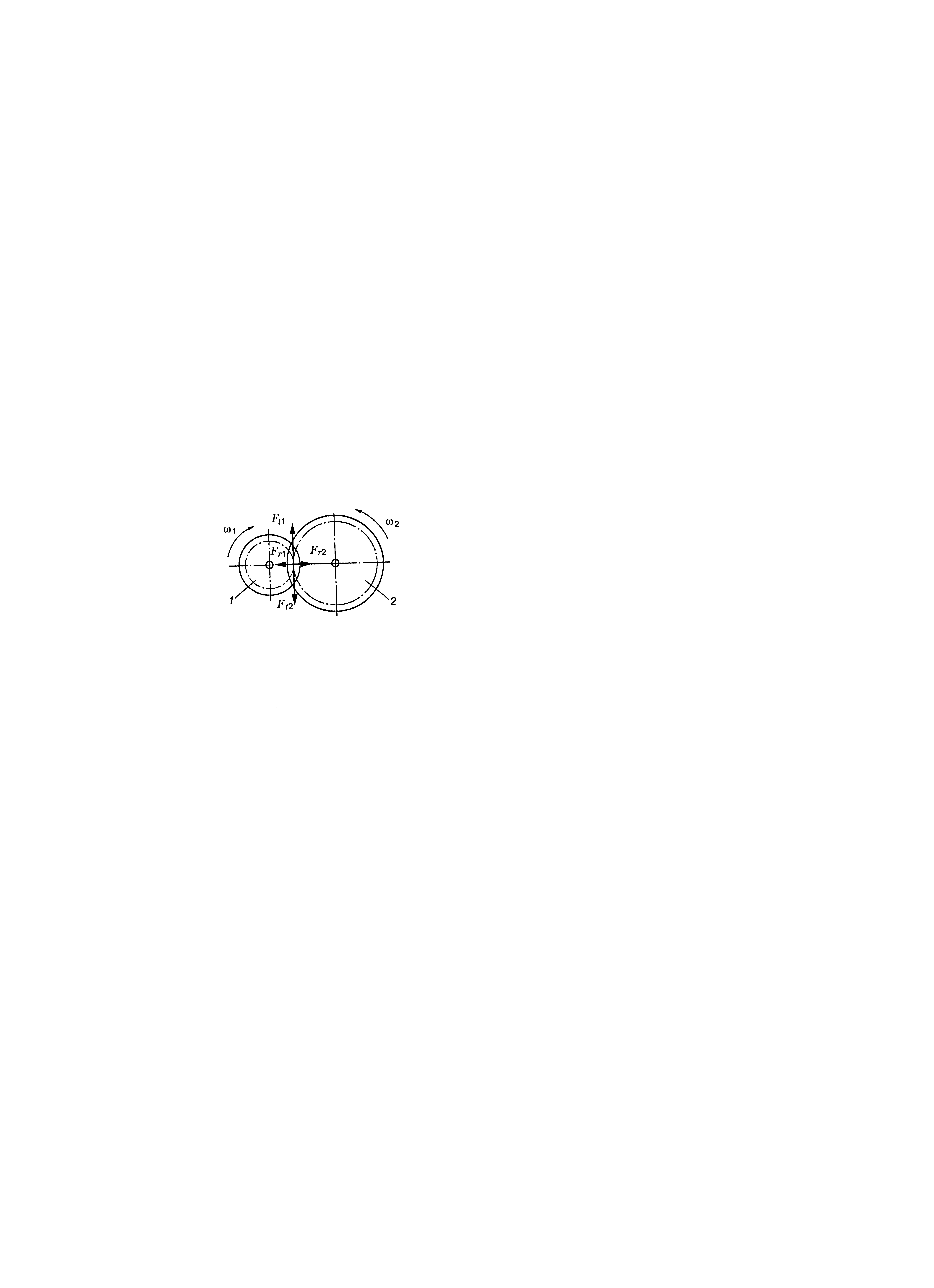
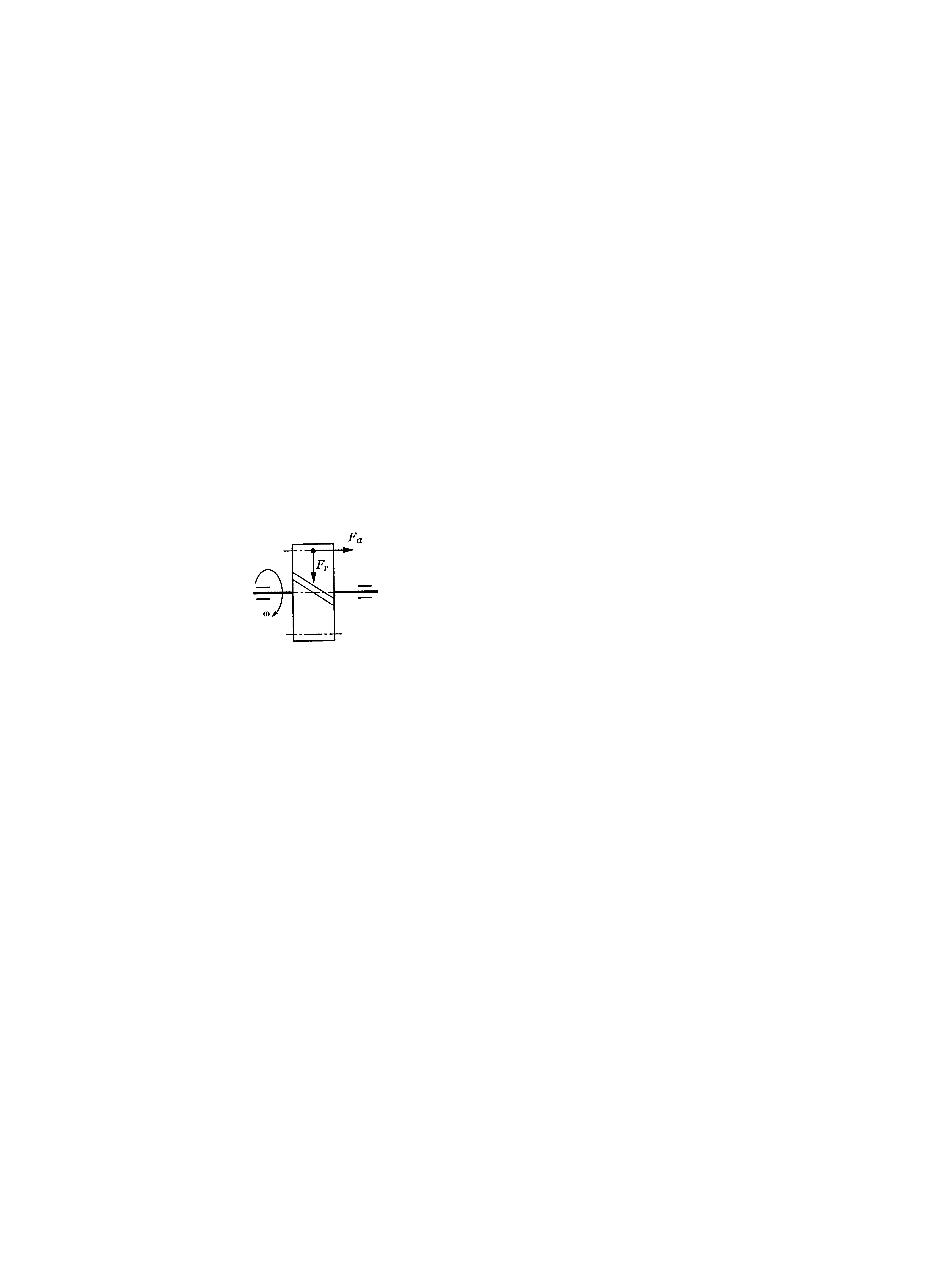
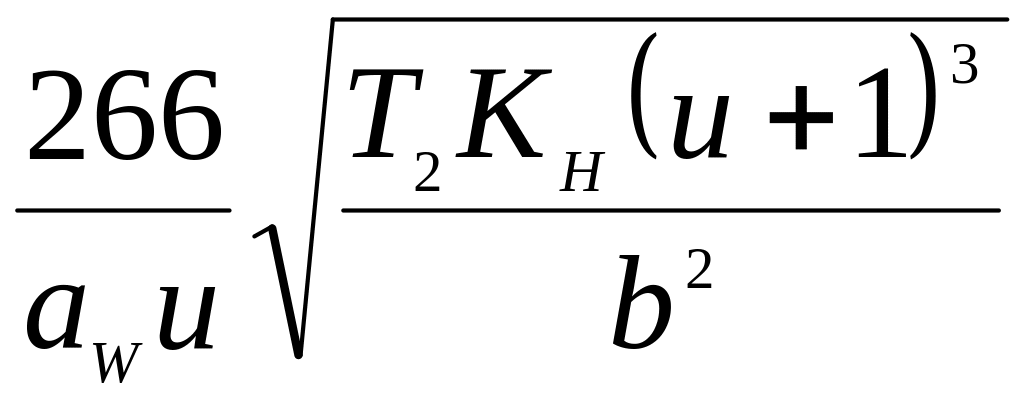 ;
б)
;
б)
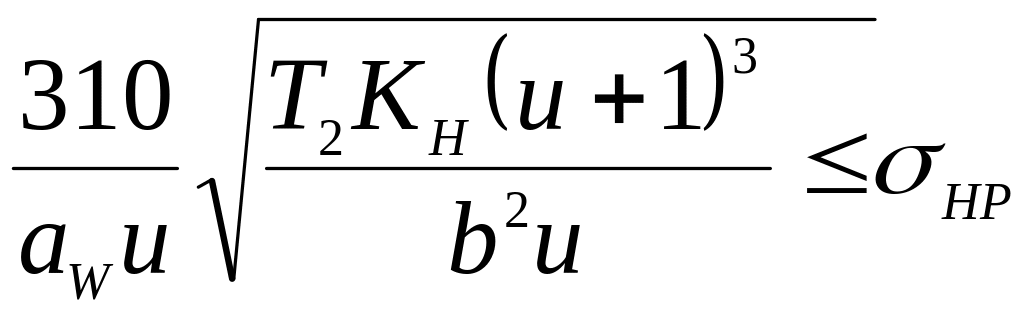 ;
;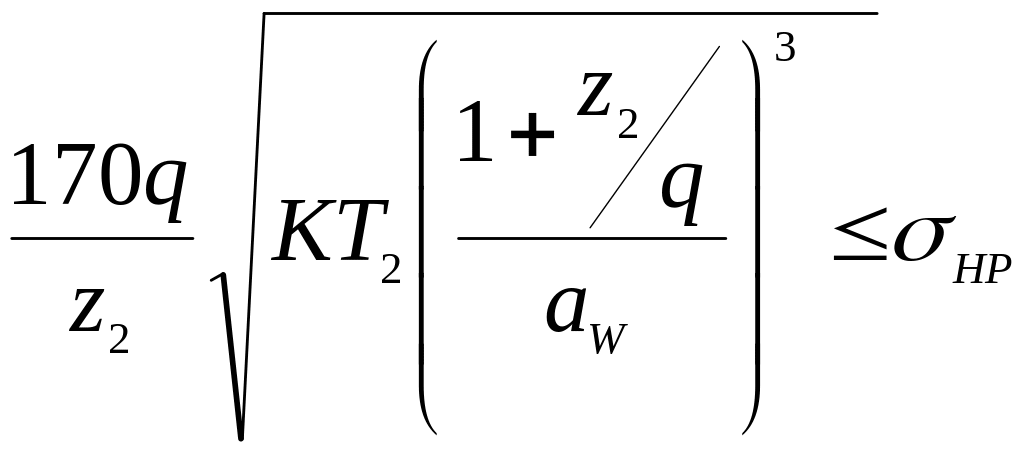 ;
г)
;
г)
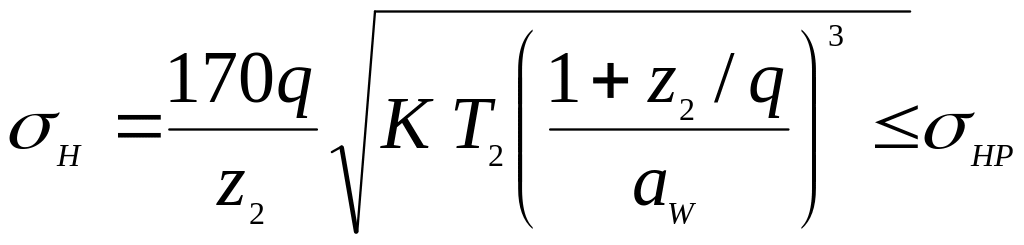

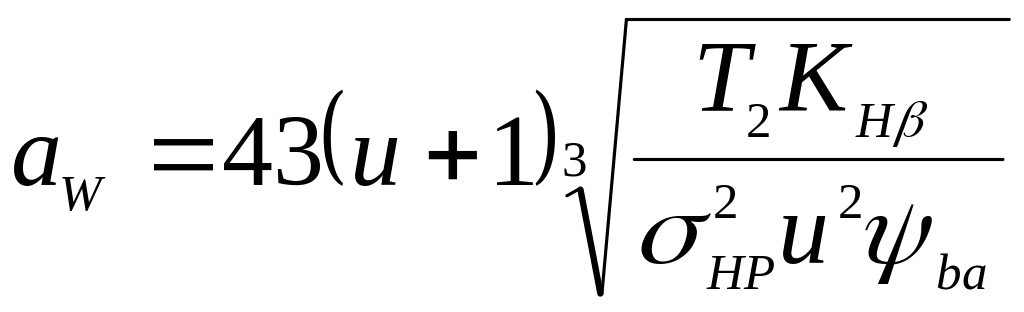 ;
б)
;
б)
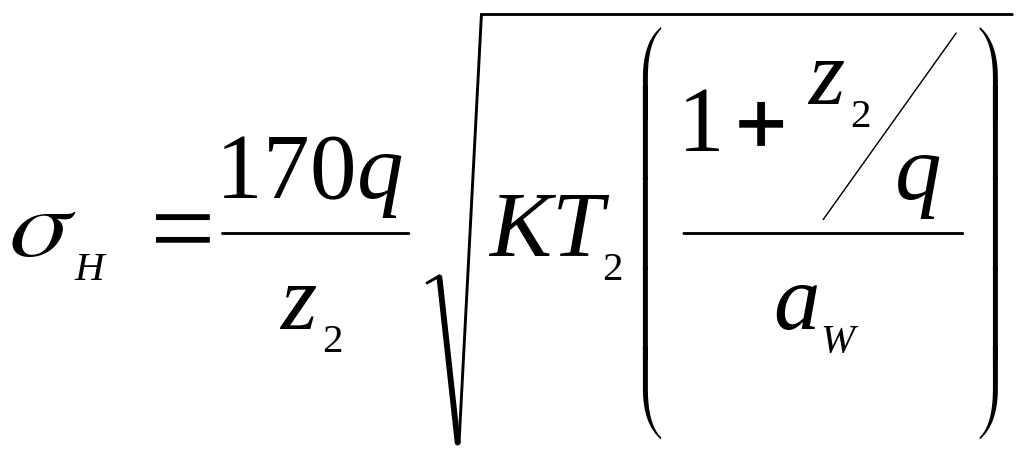 ;
;
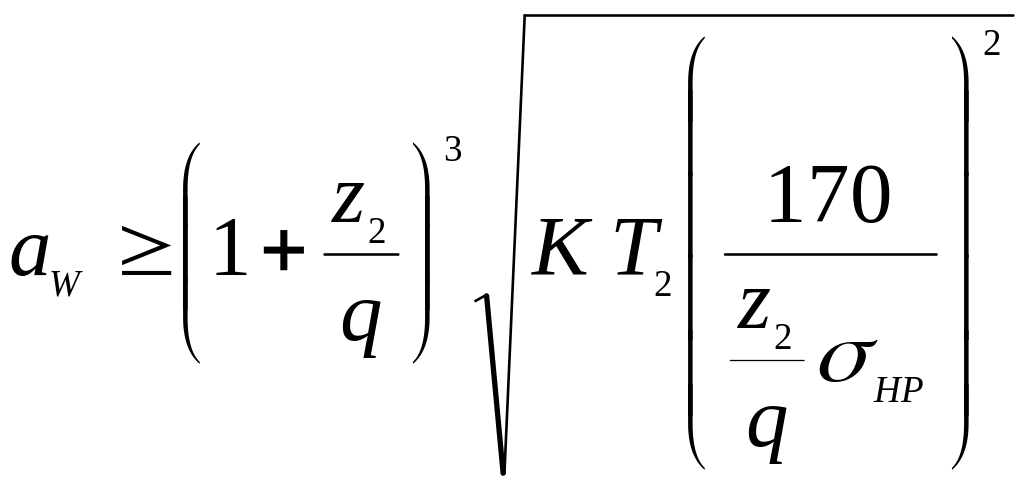 ;
г)
;
г)
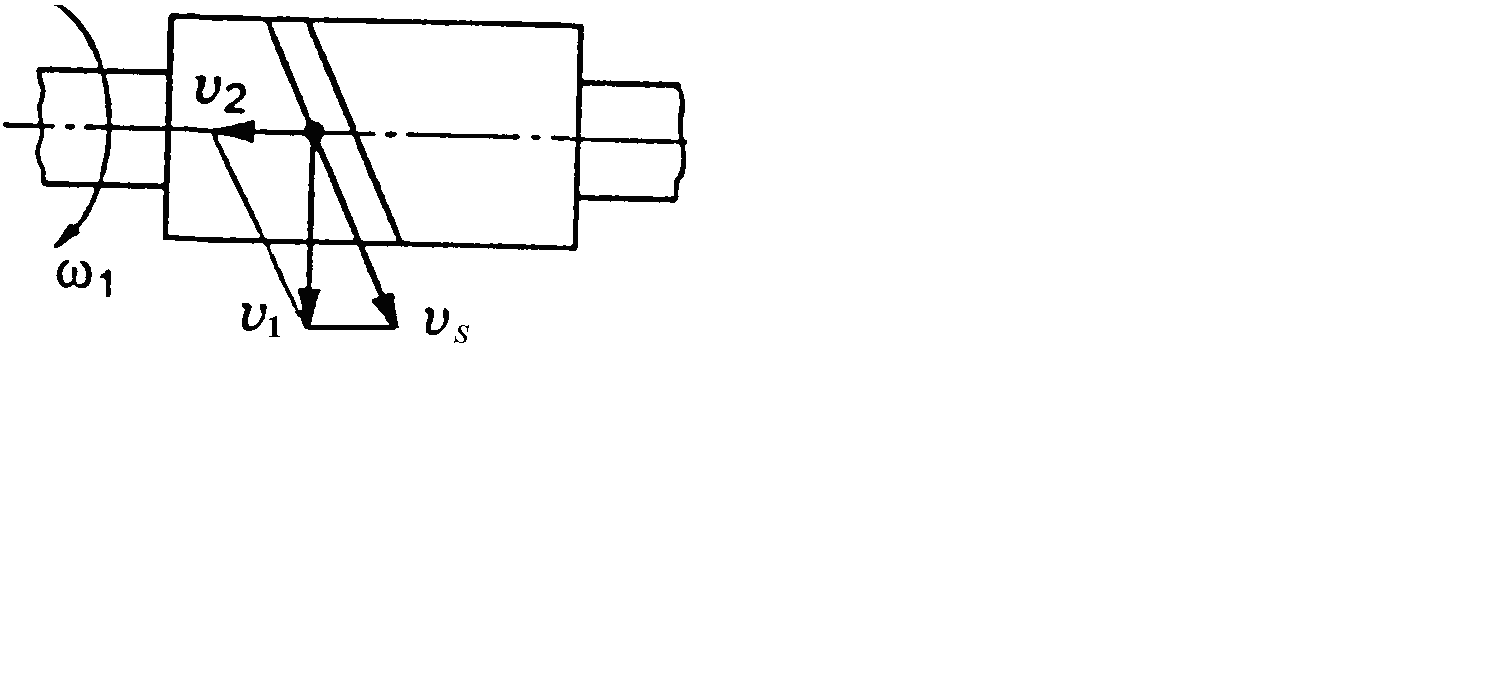
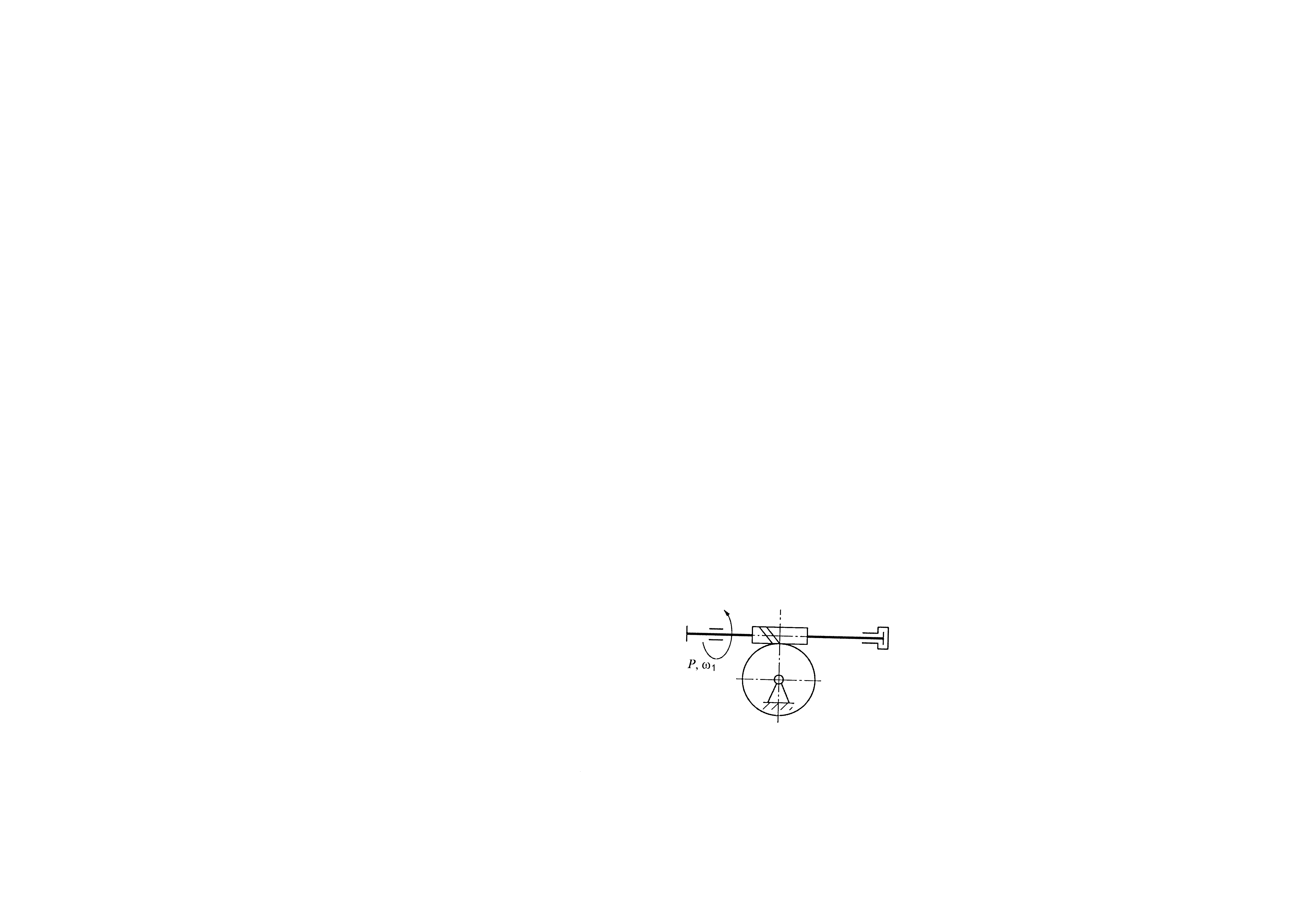
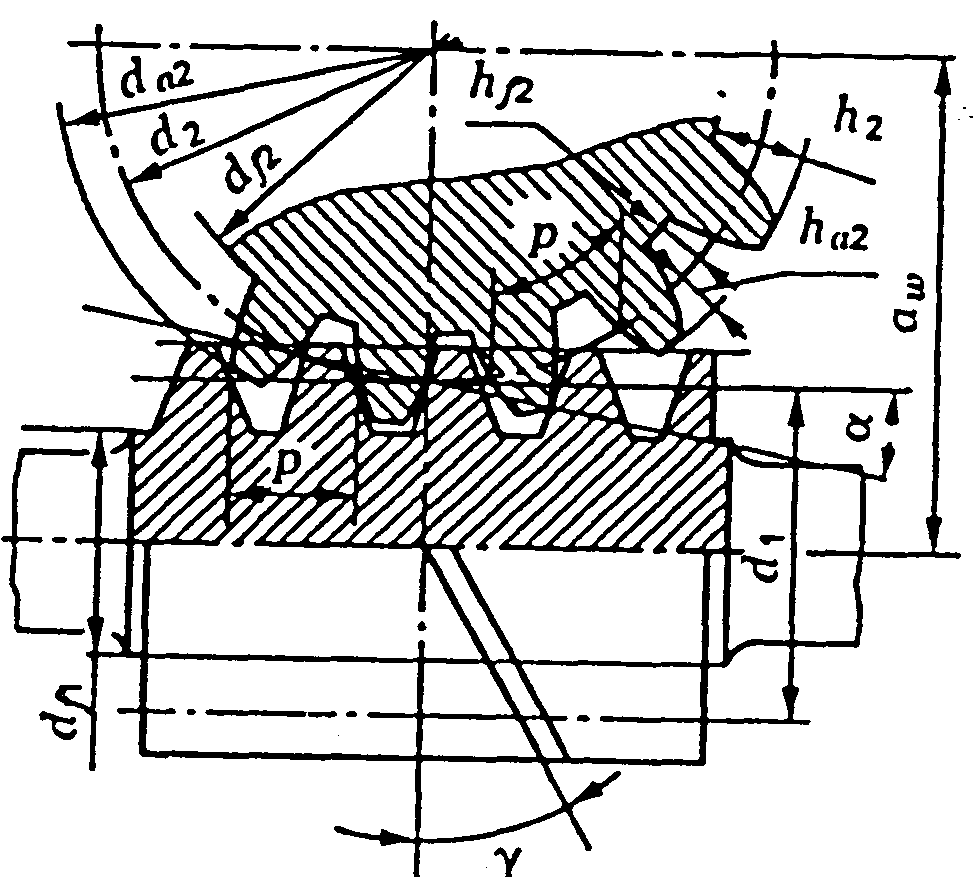
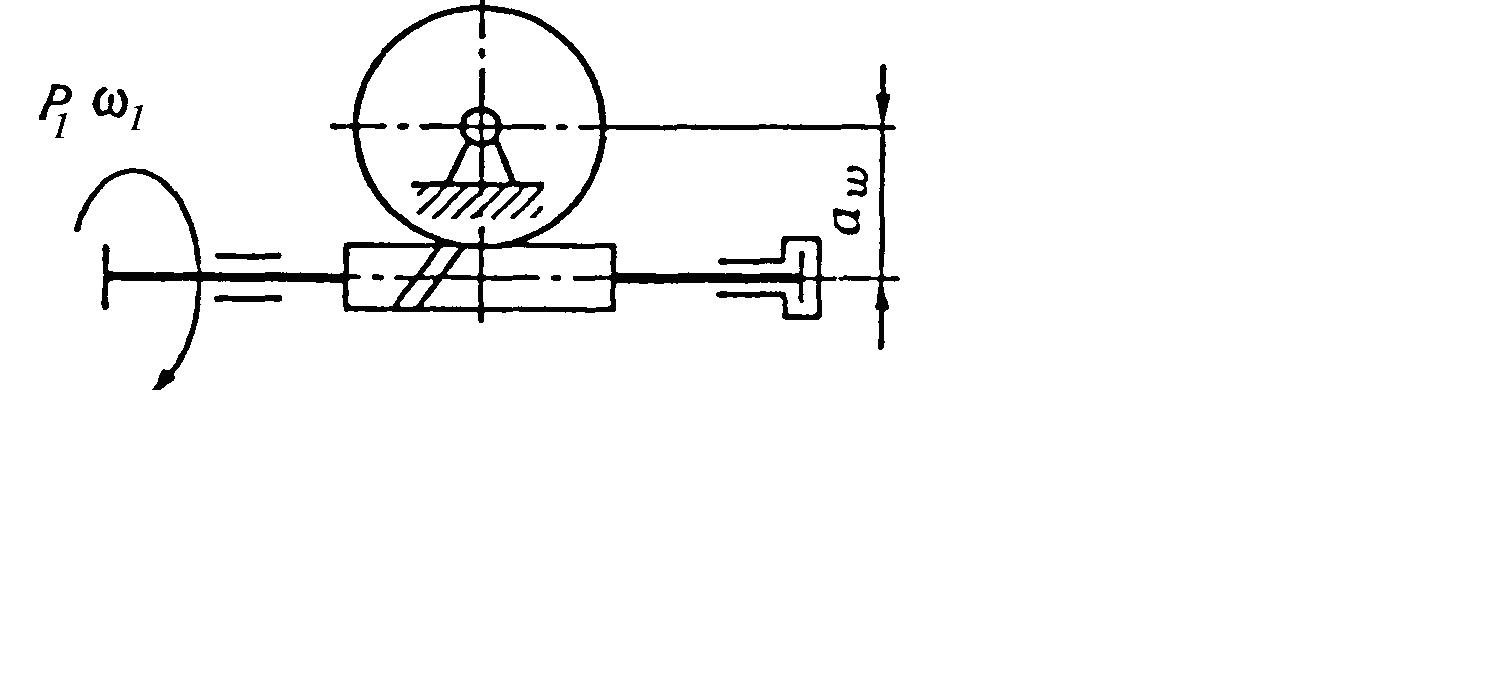
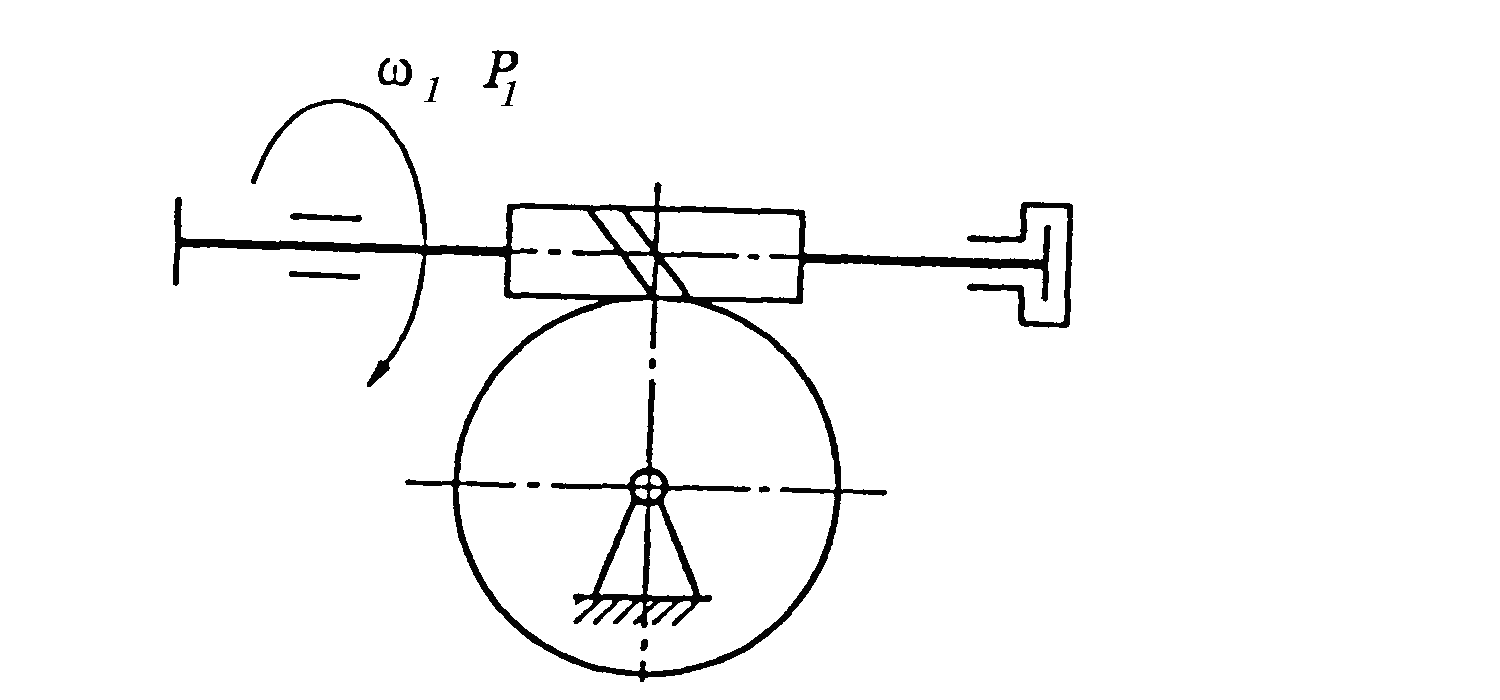
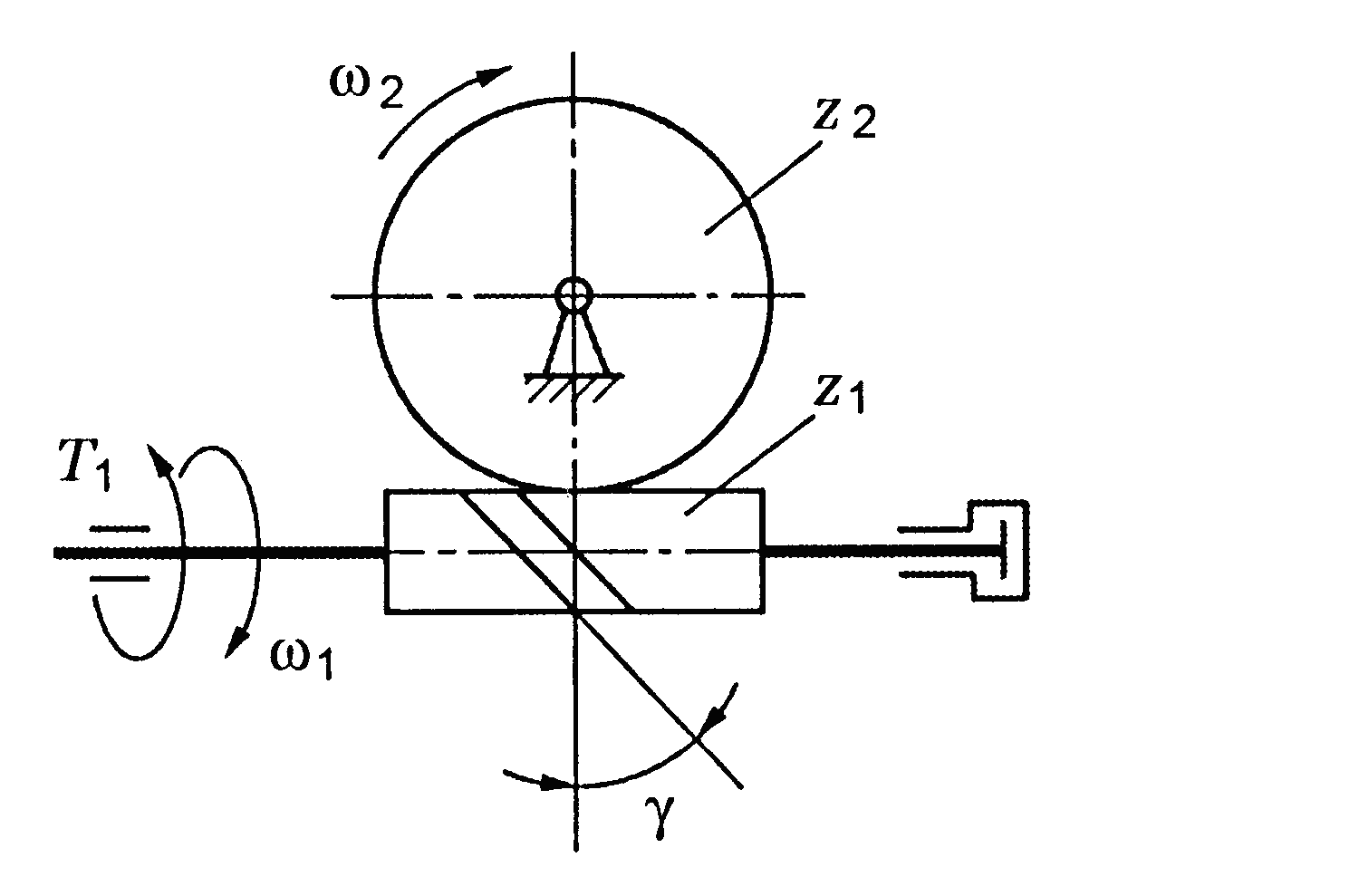
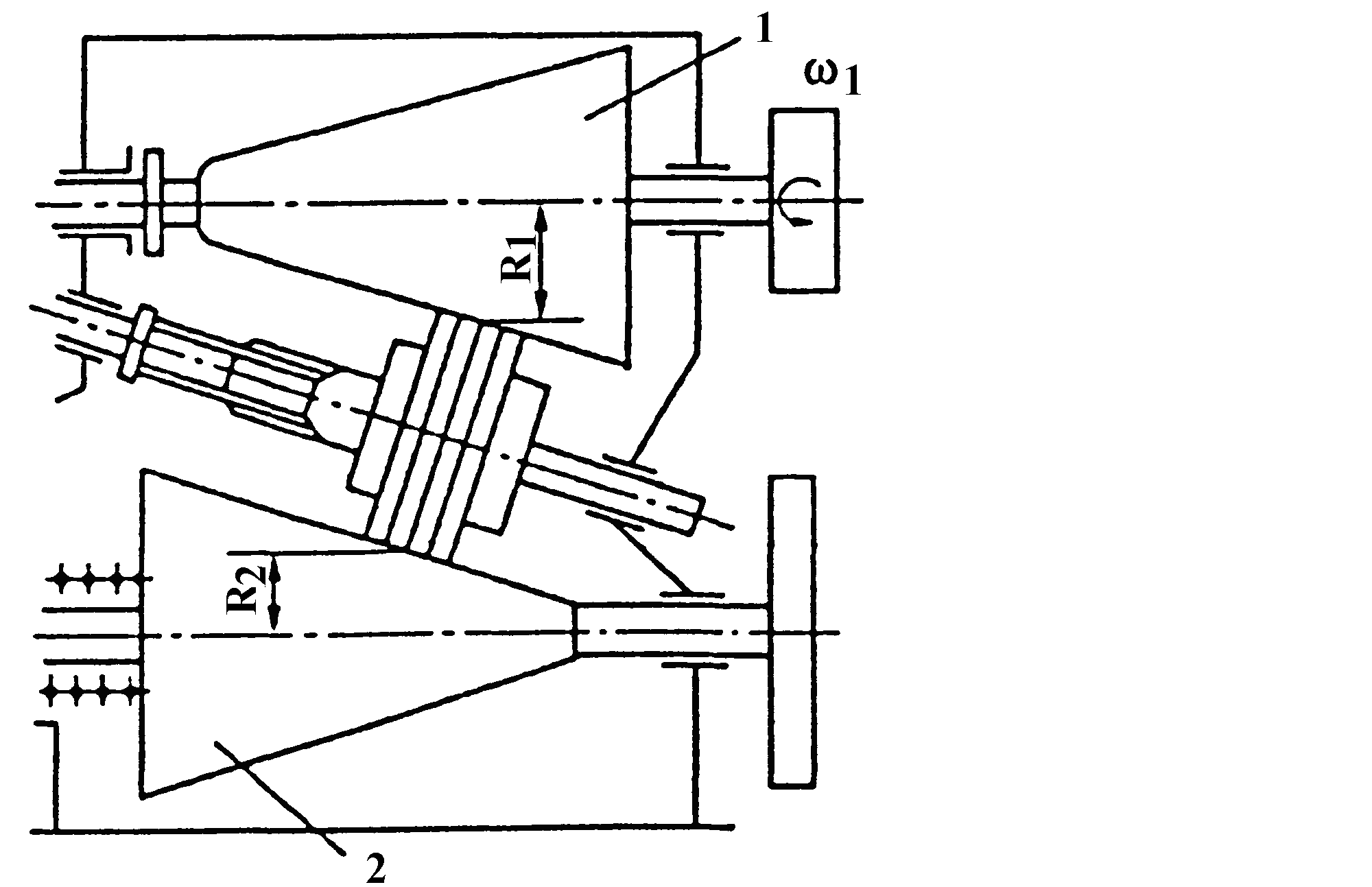
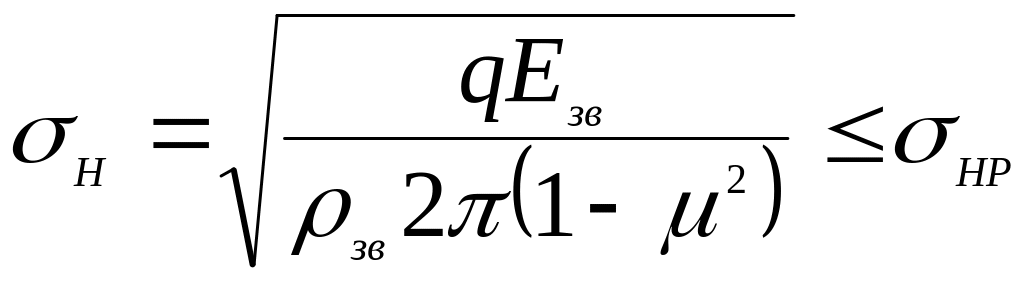 ;
б)
;
б)
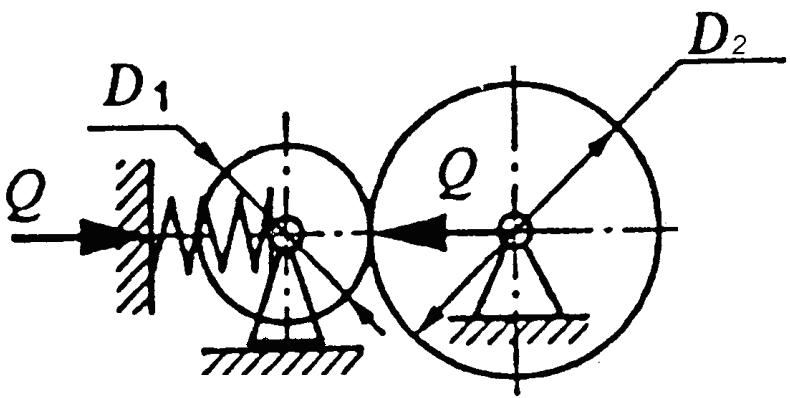
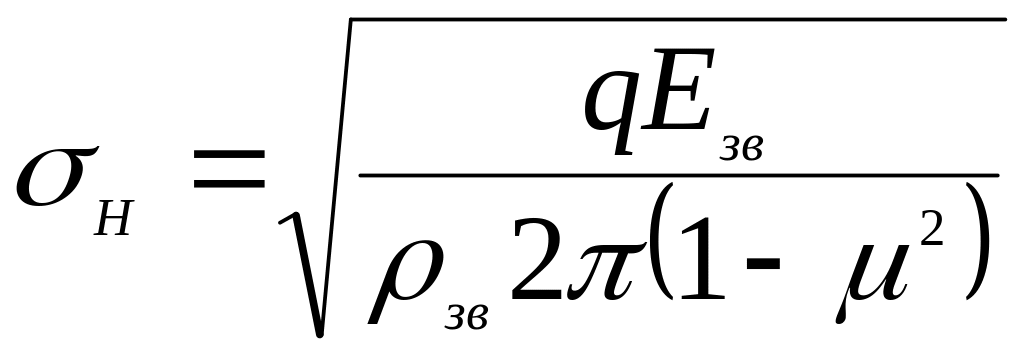
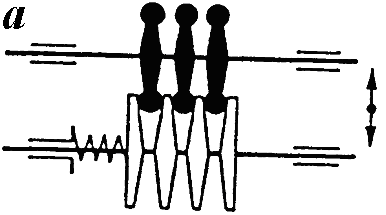
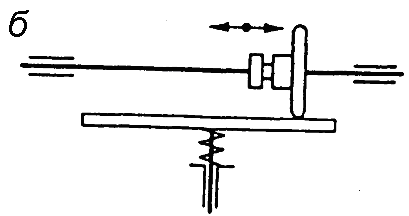
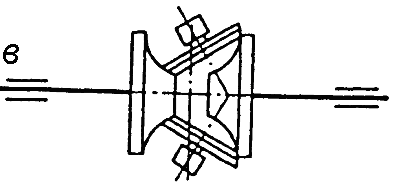
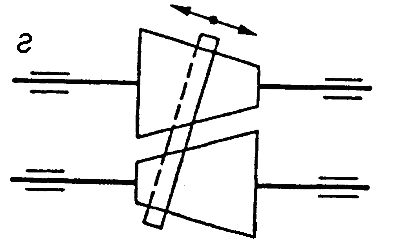
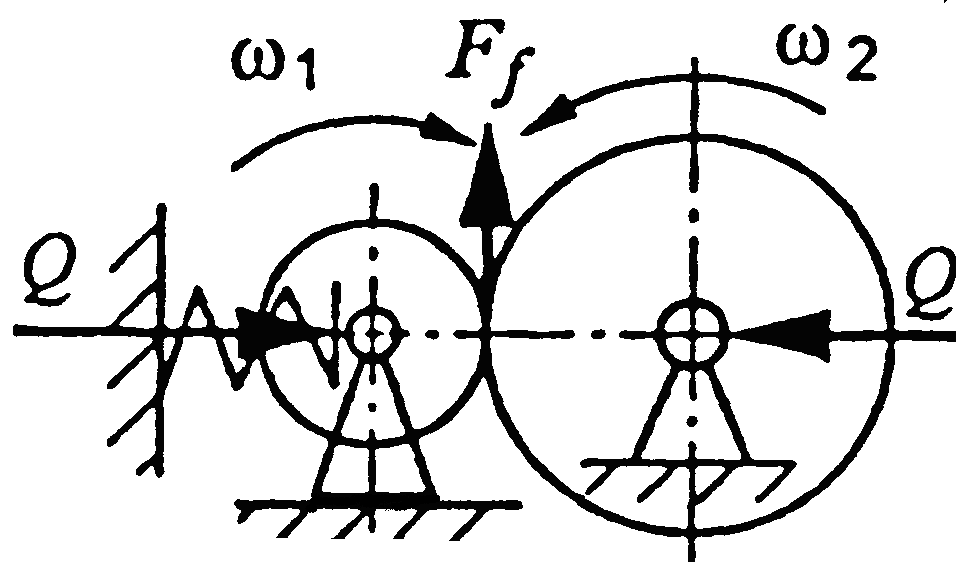
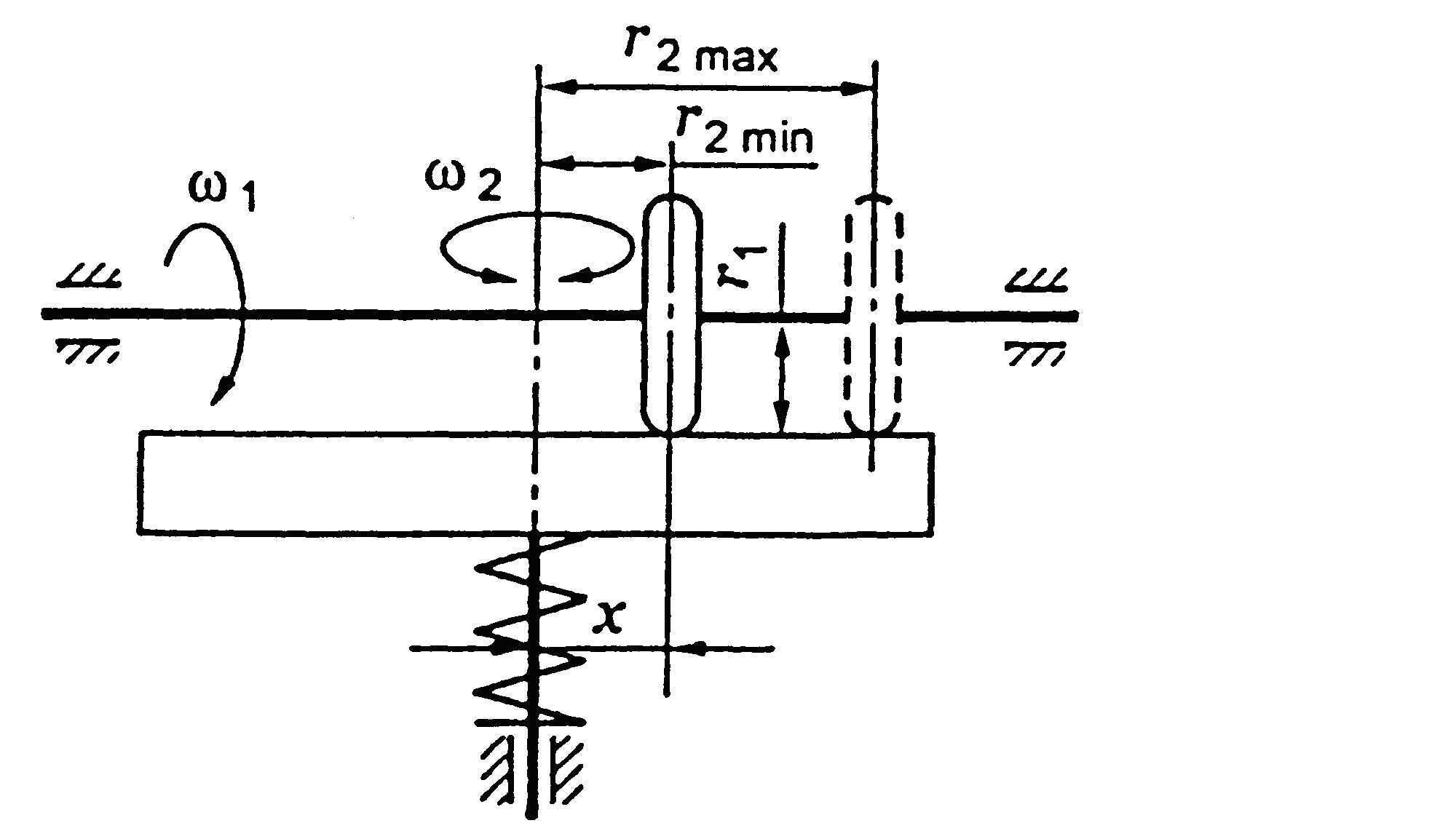
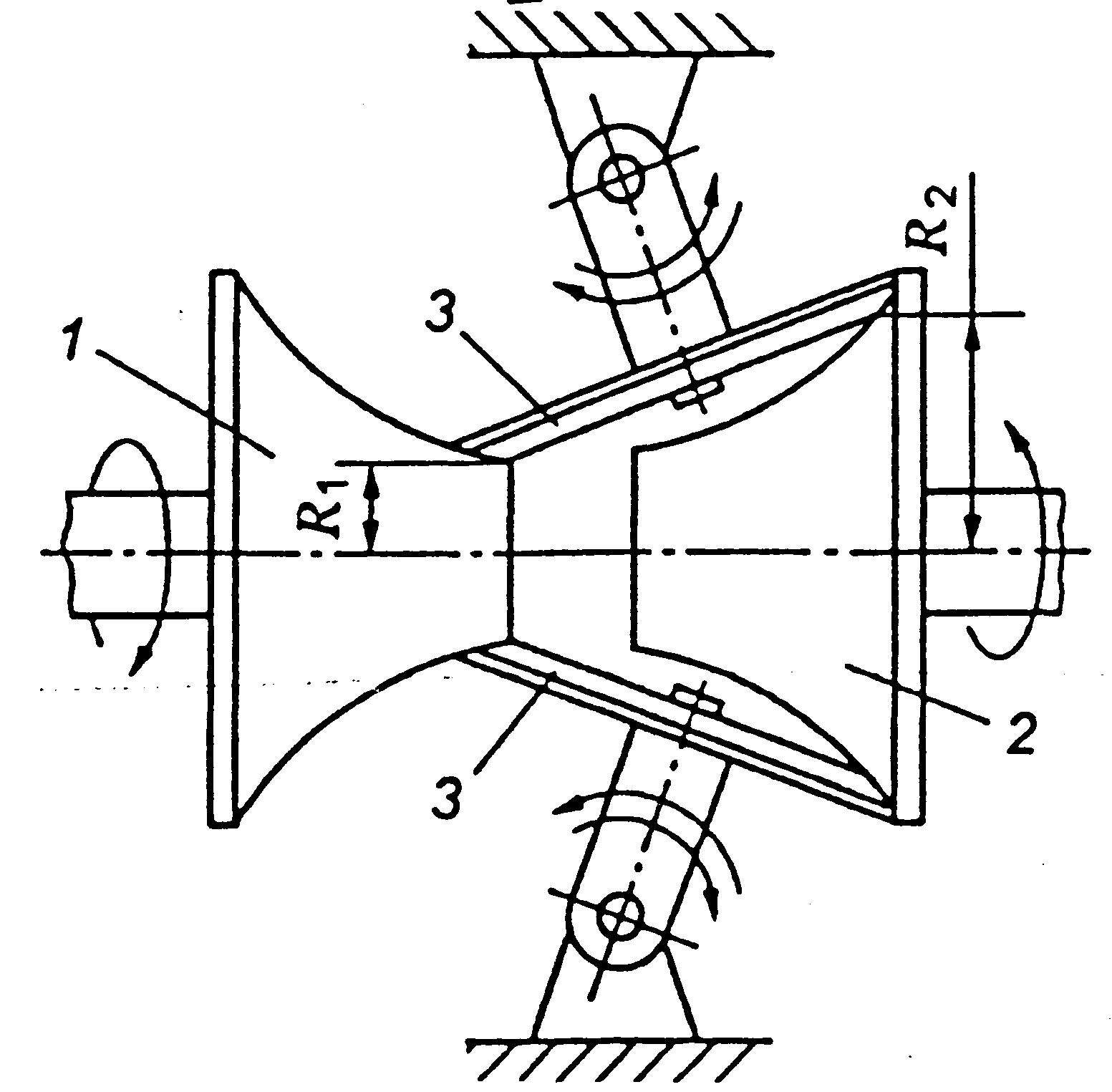
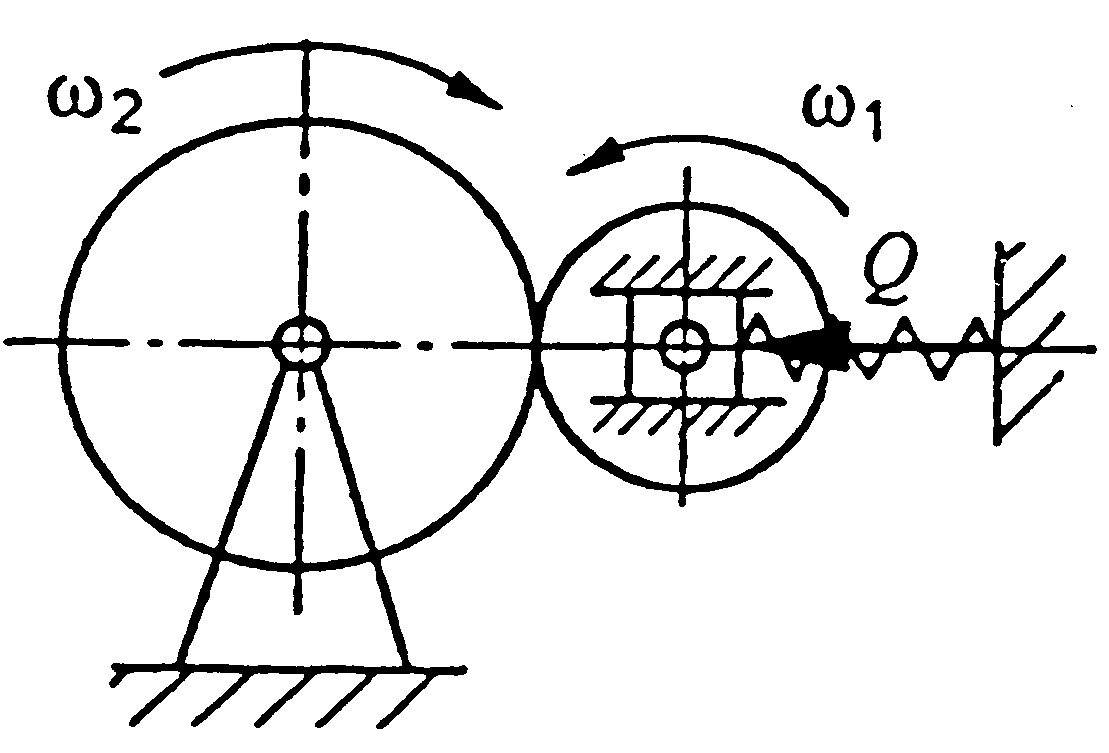
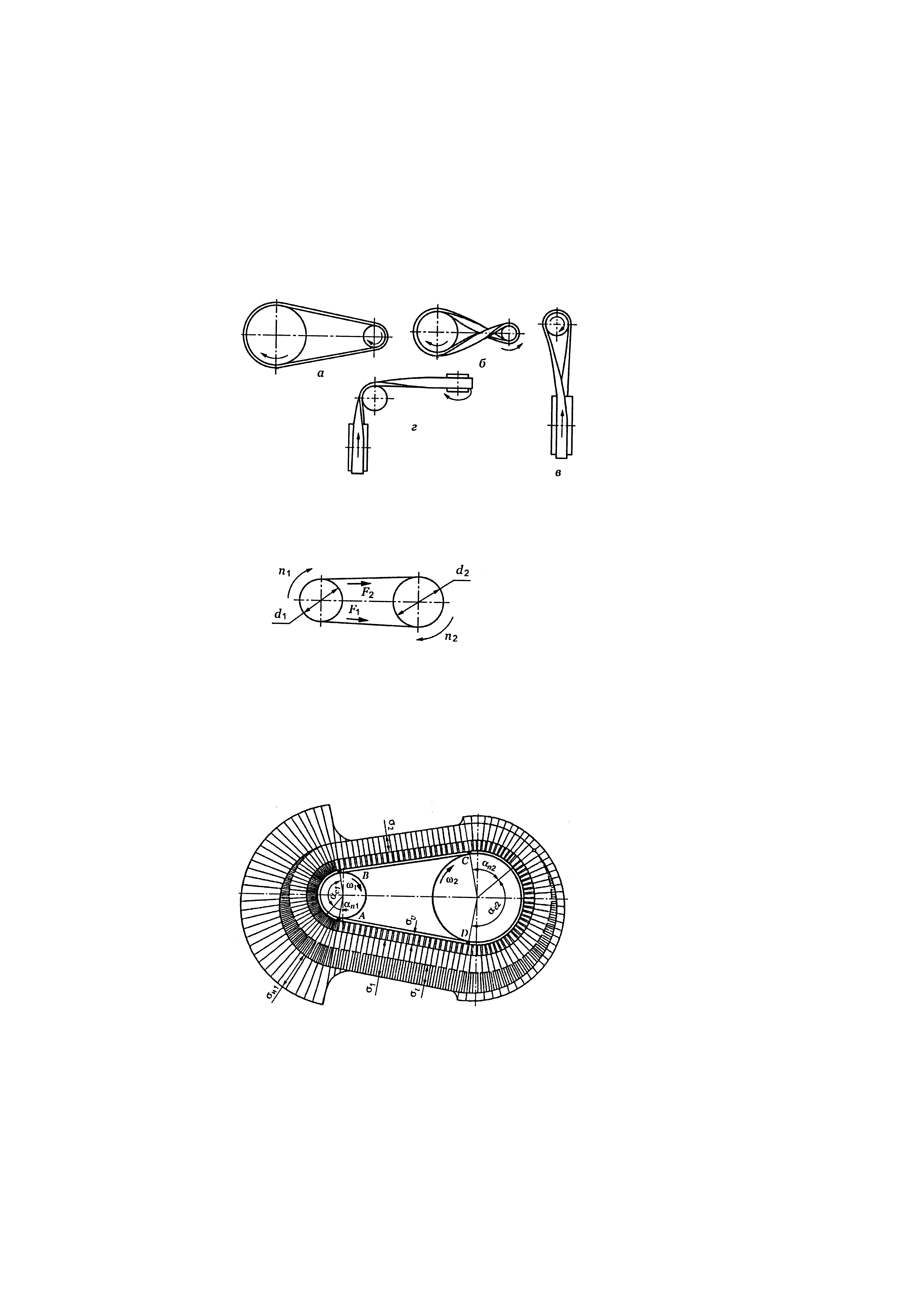
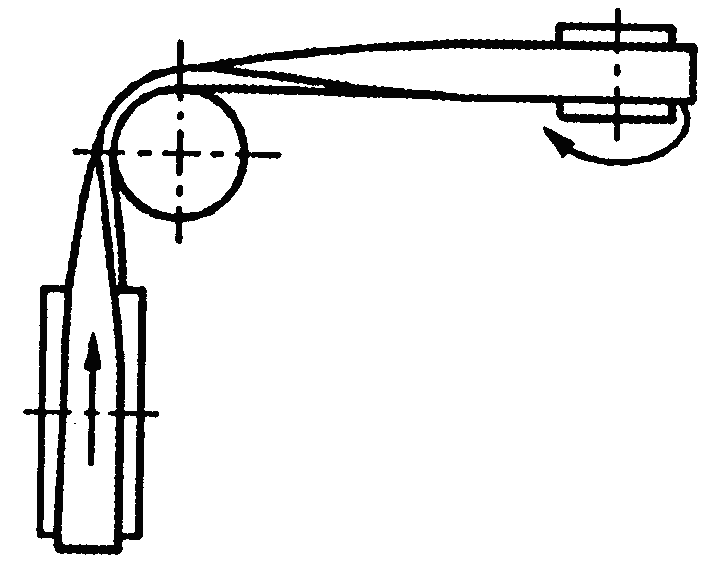
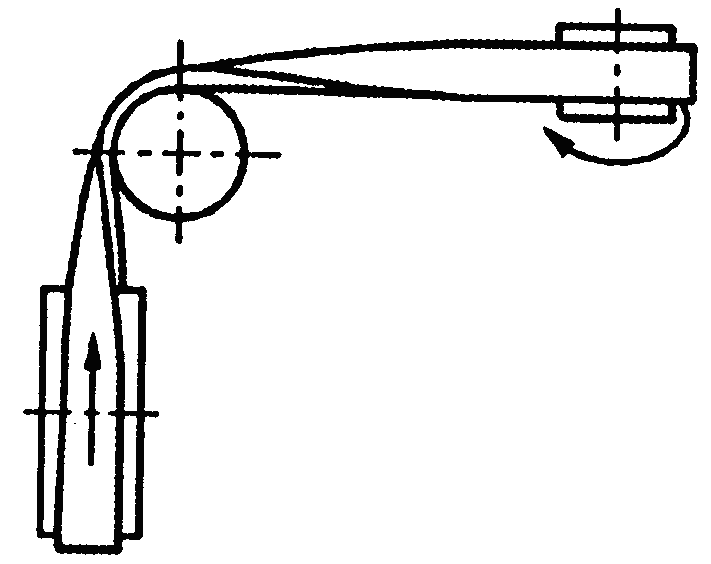
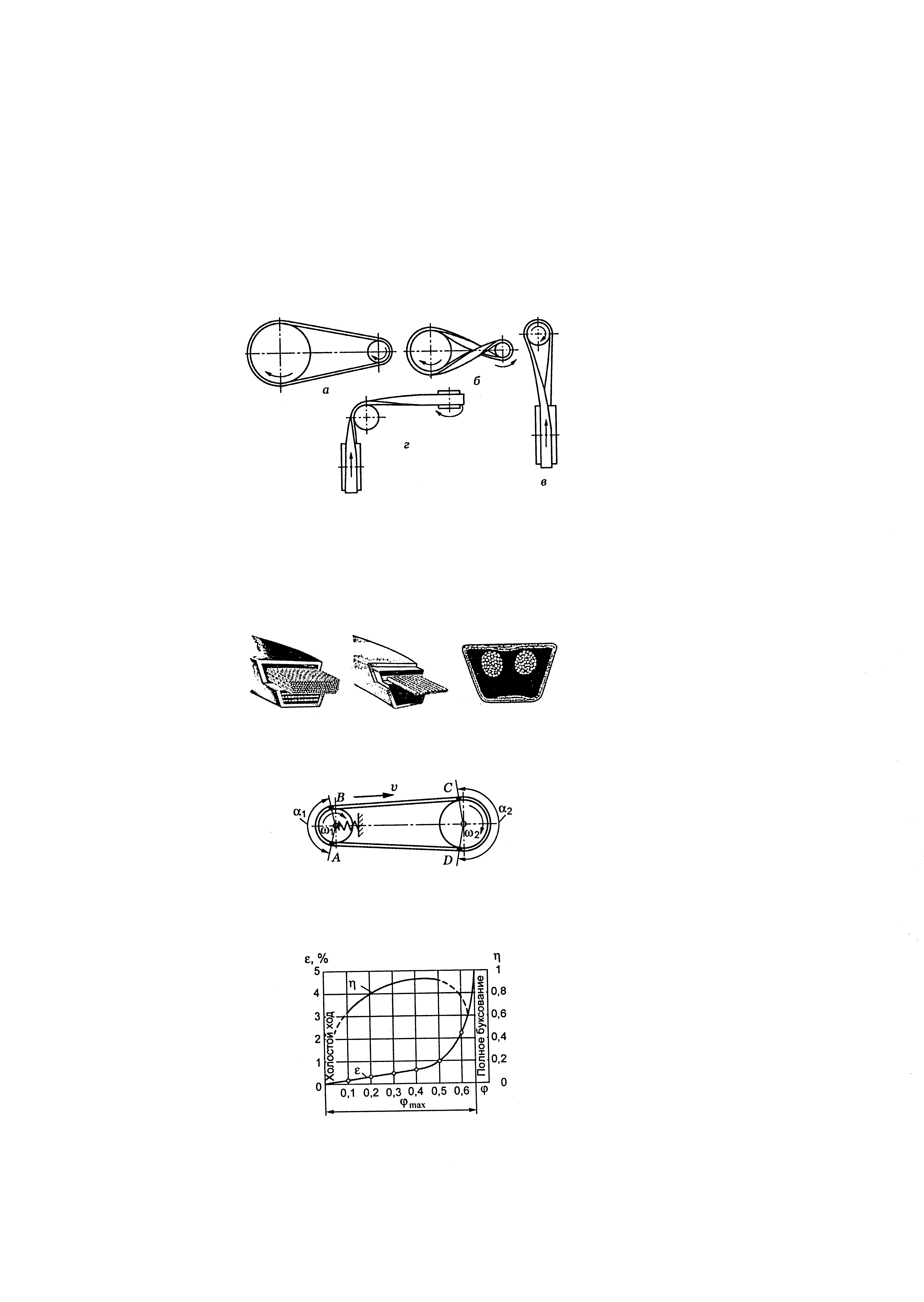
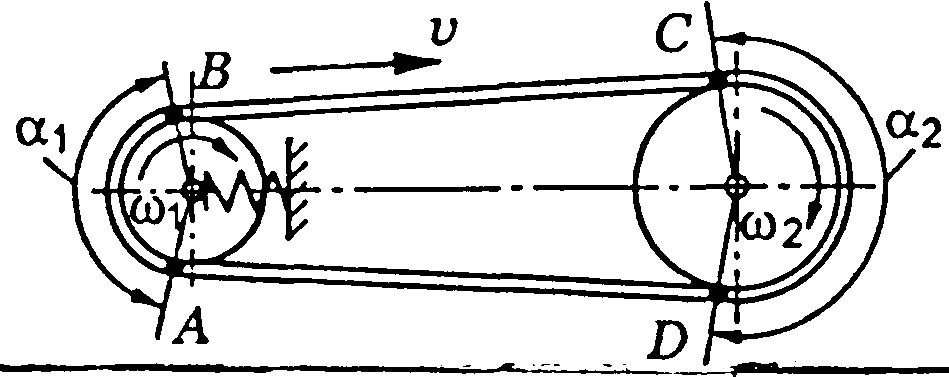
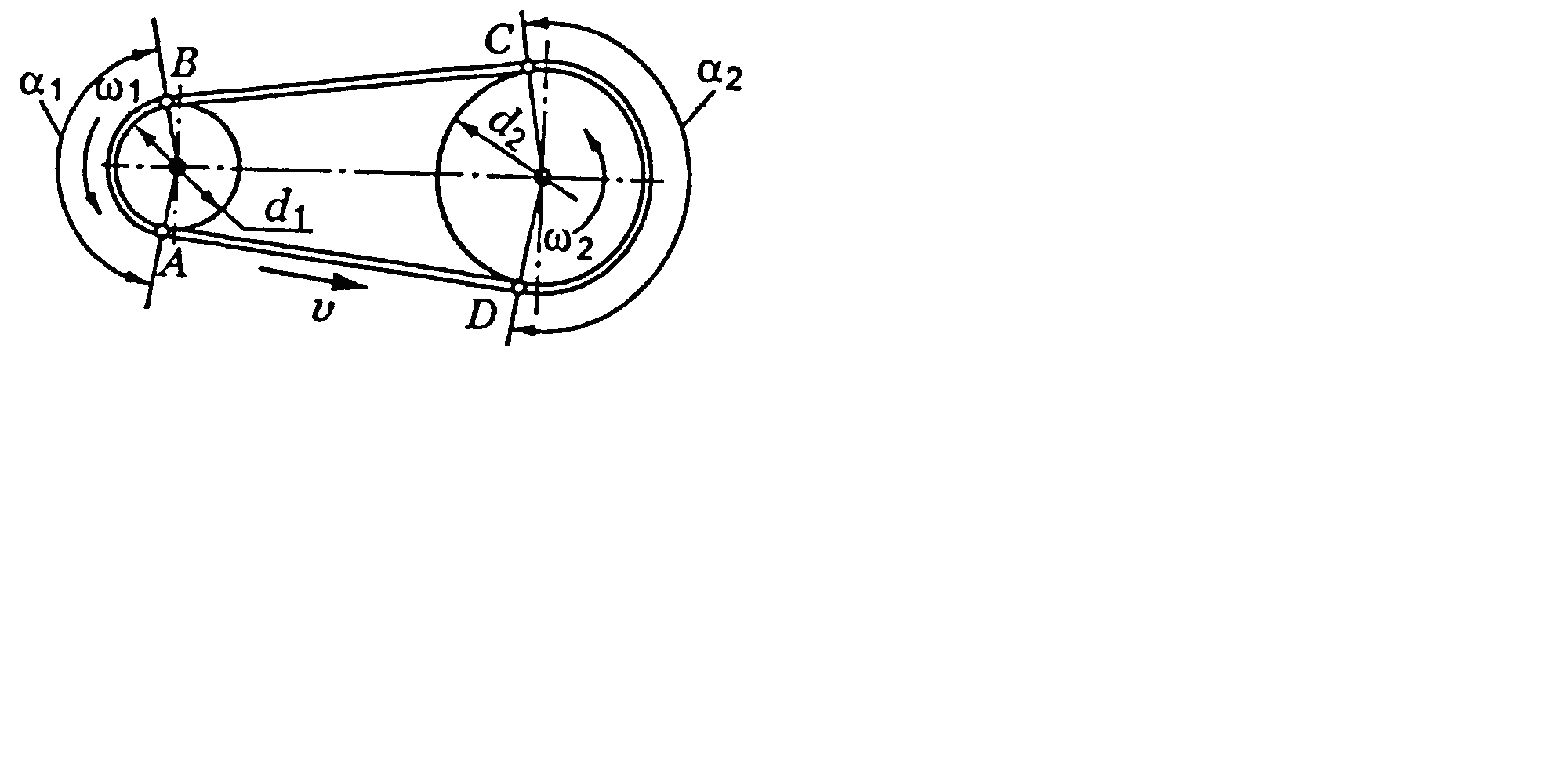
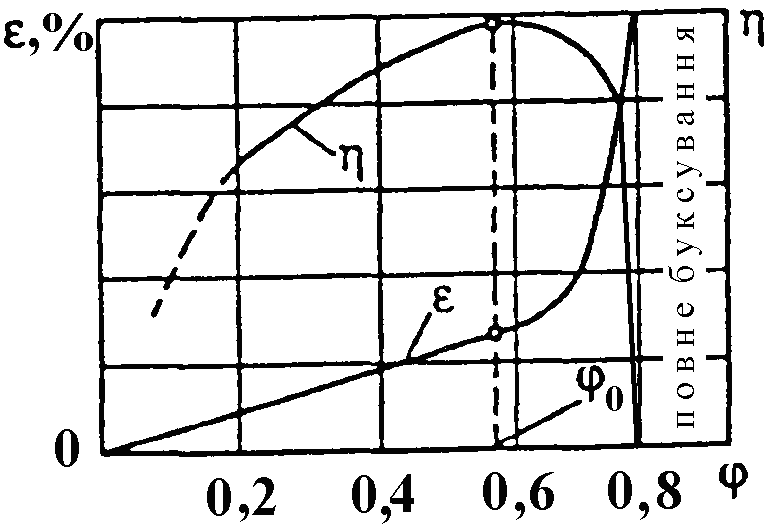
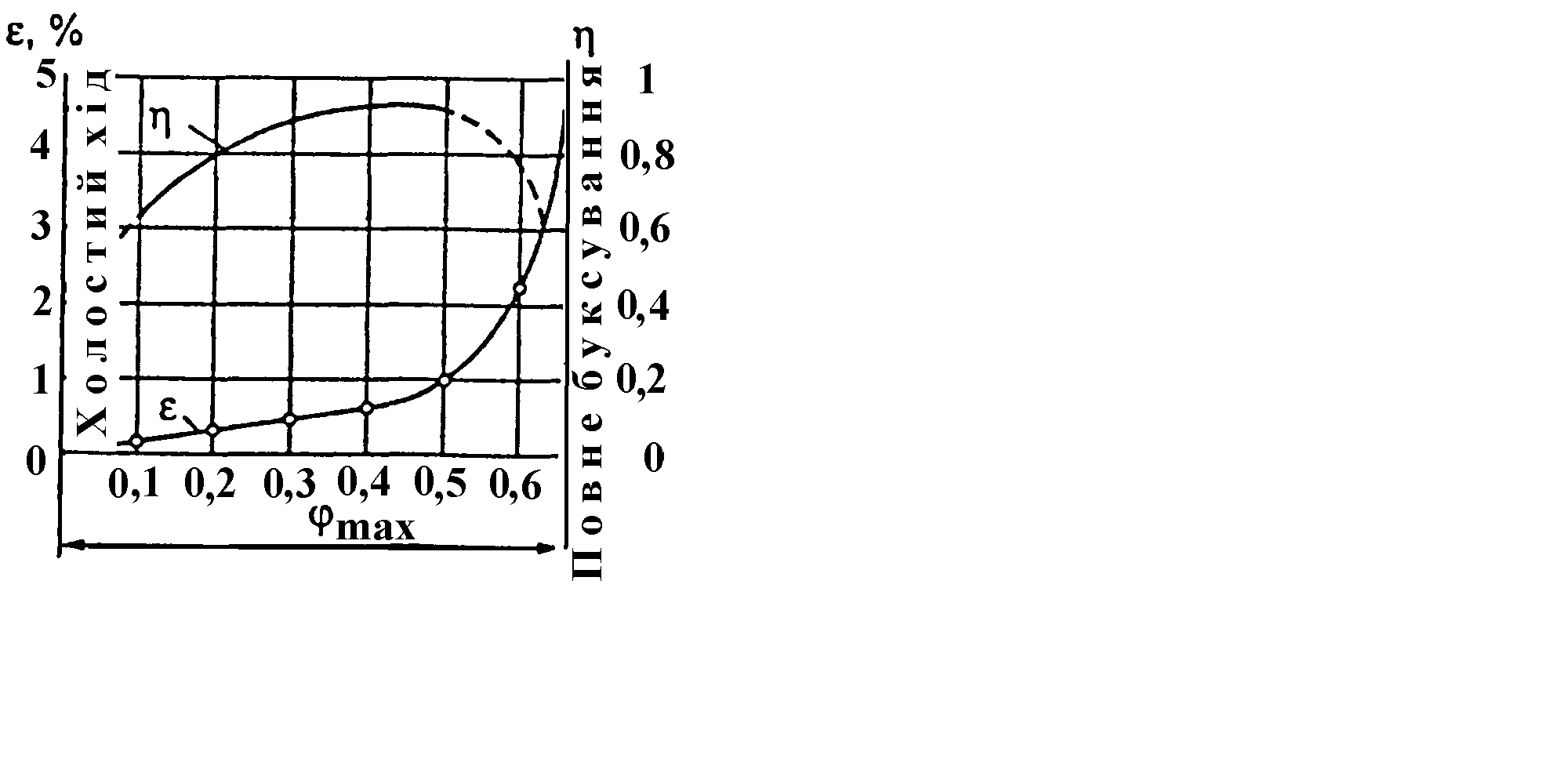
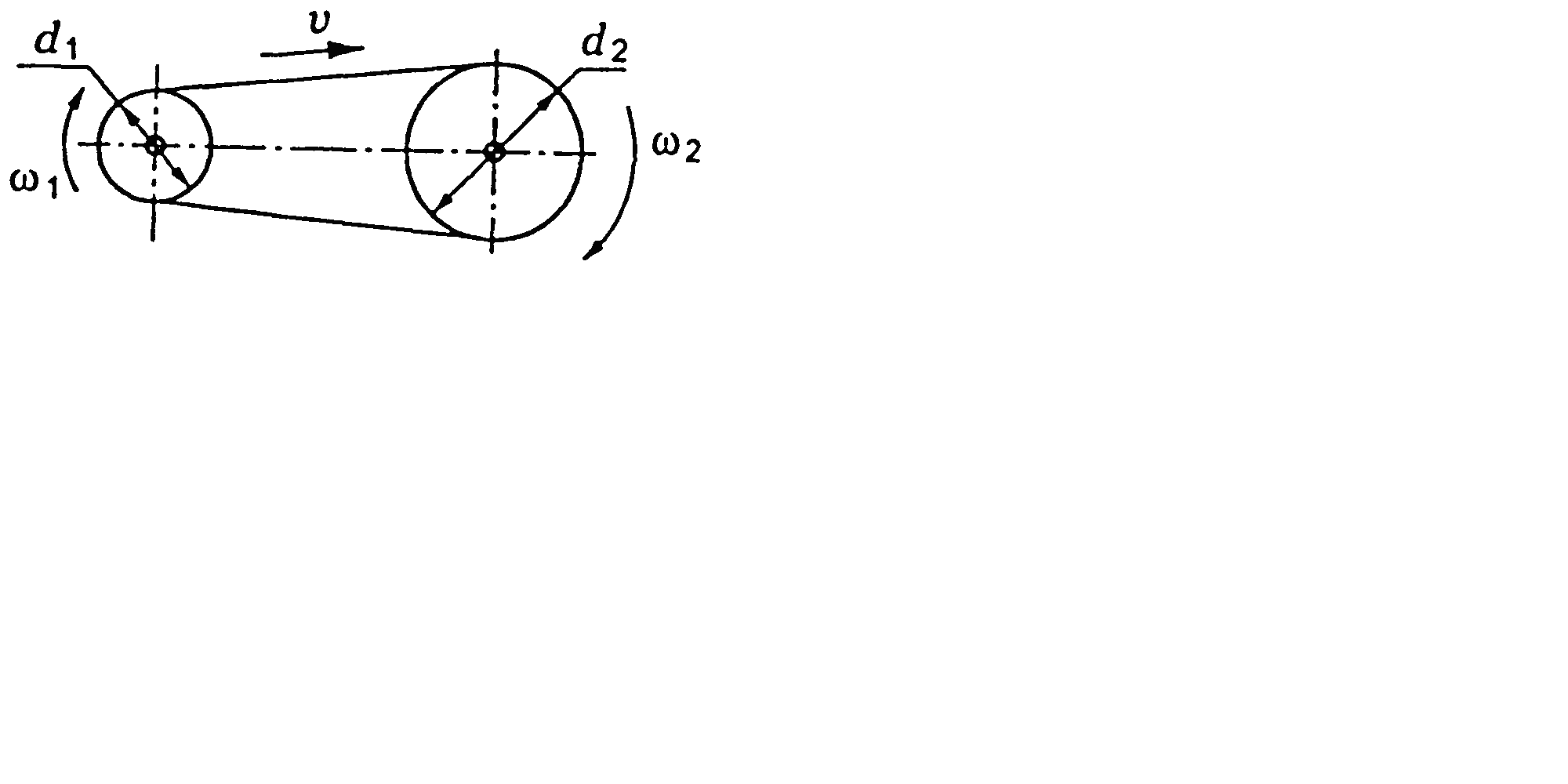
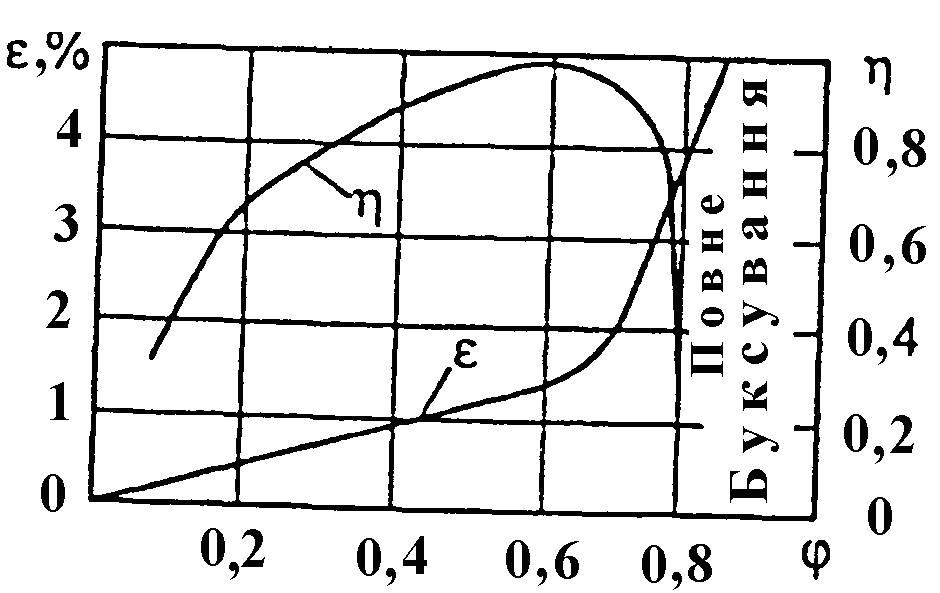
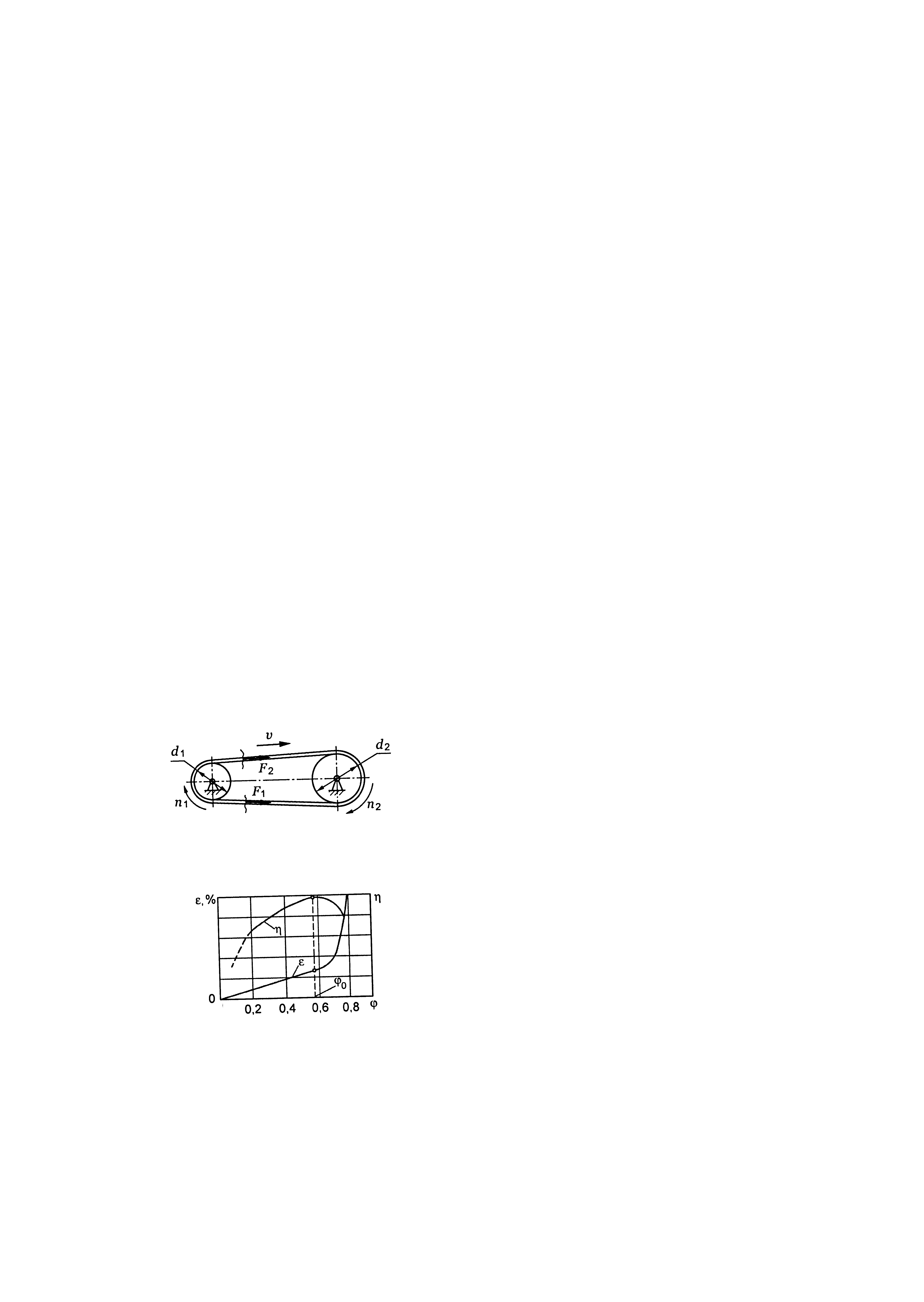
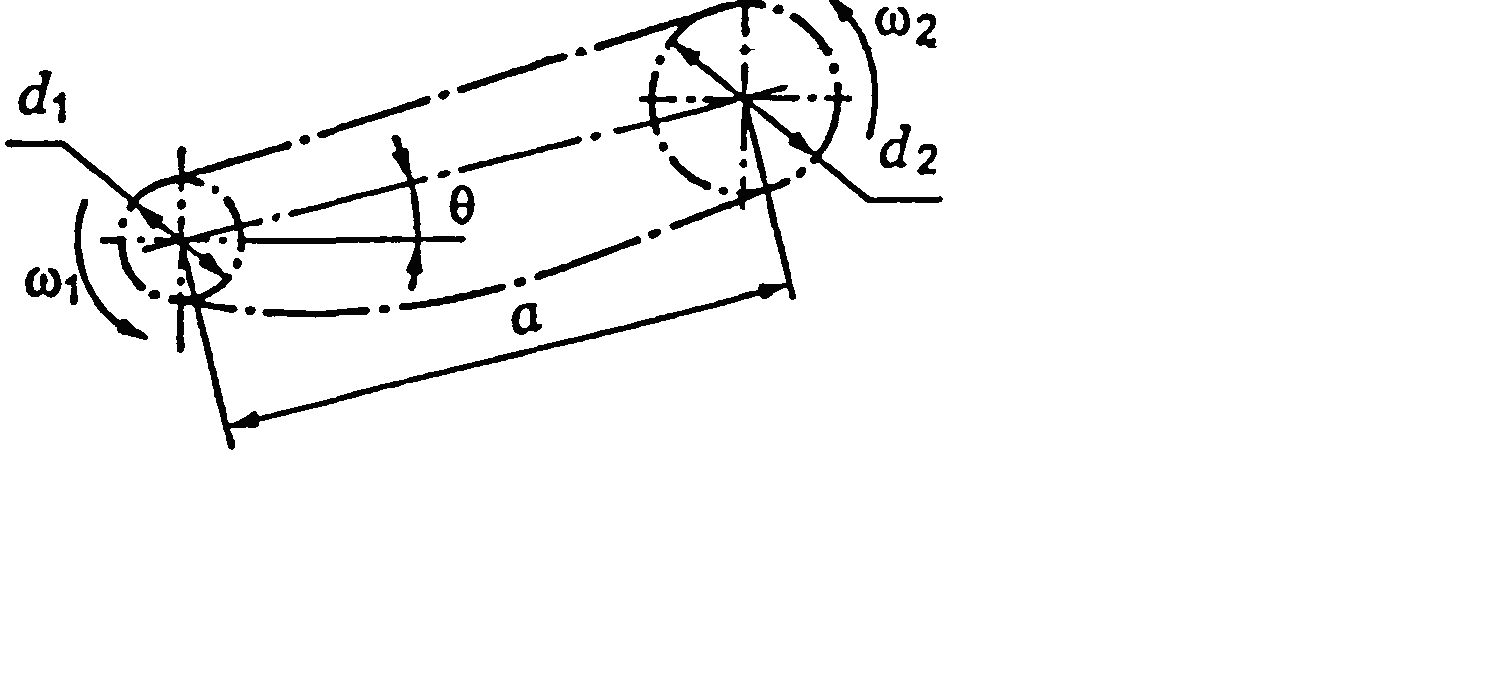
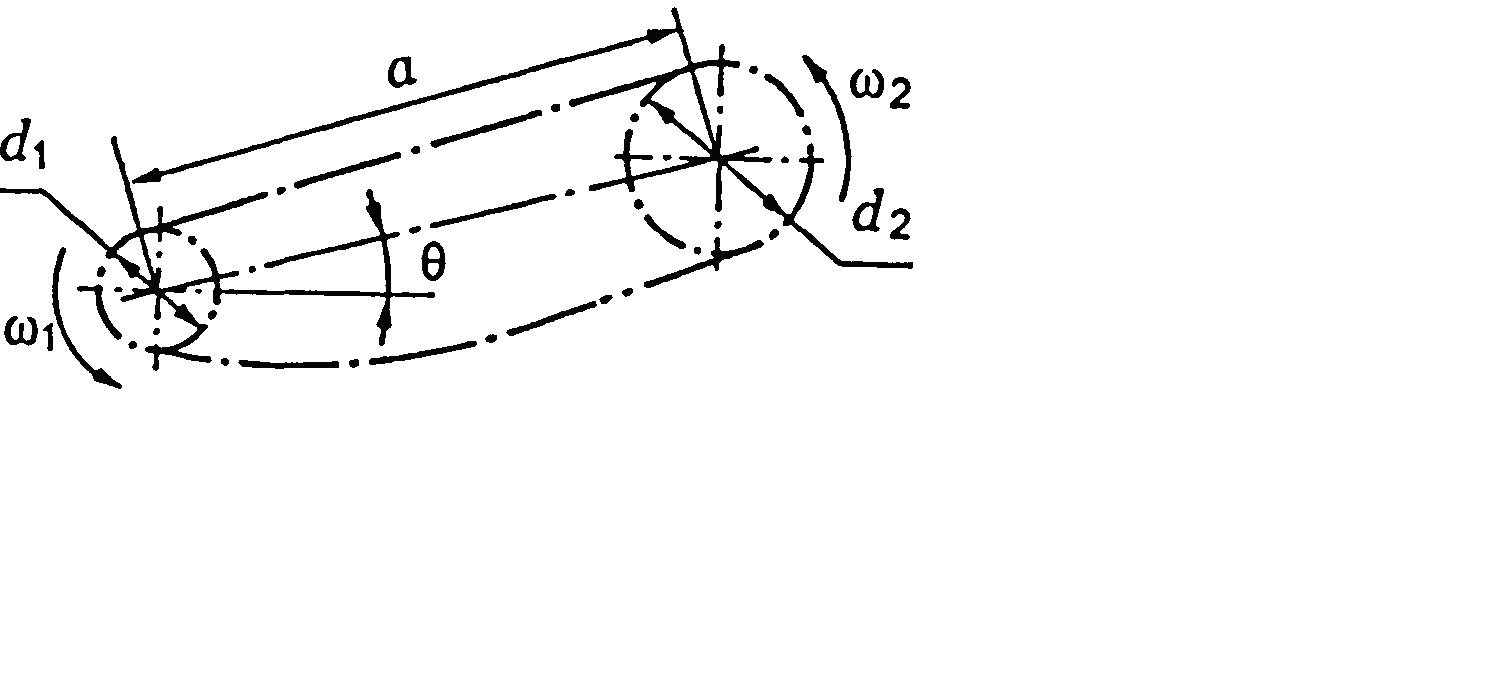
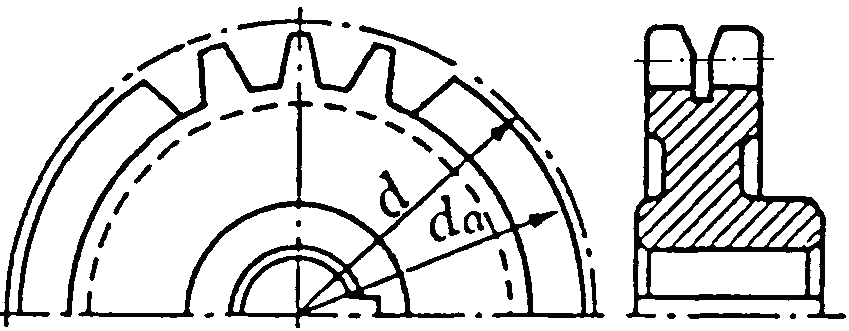
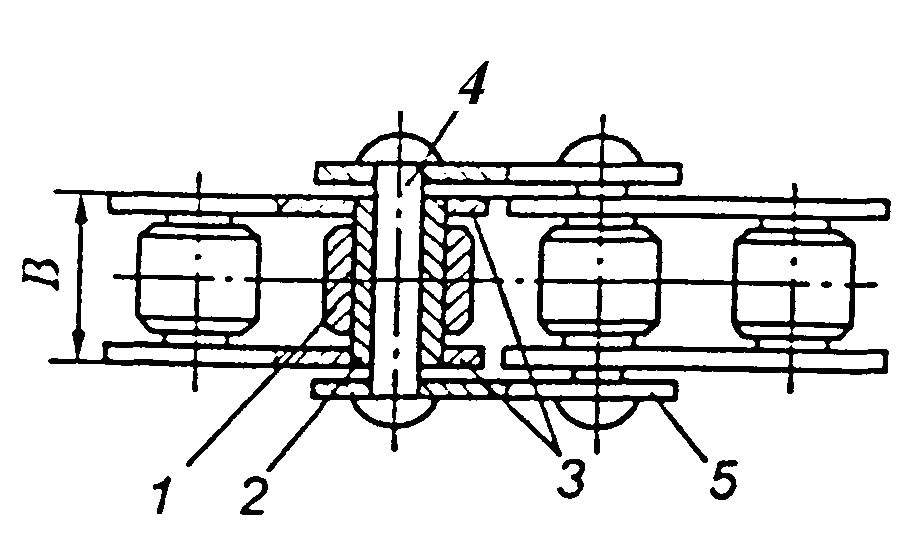
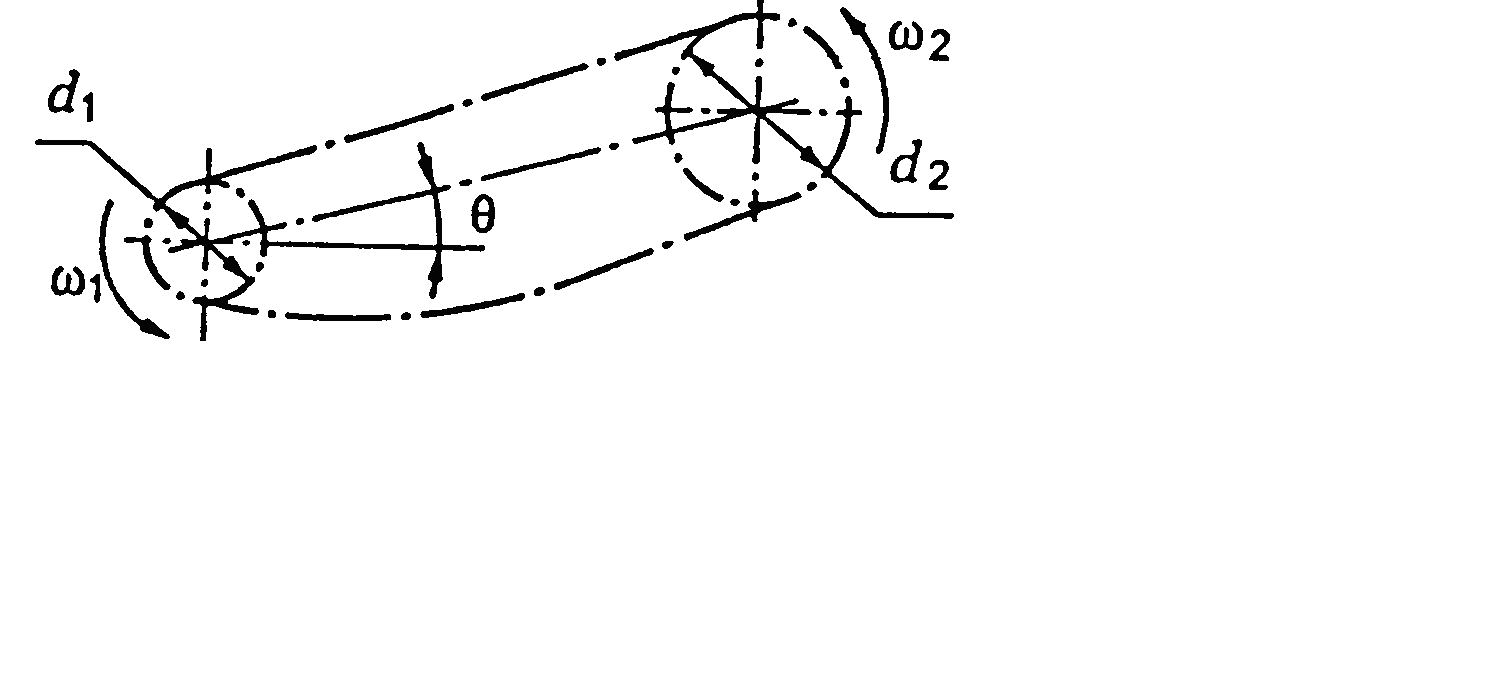
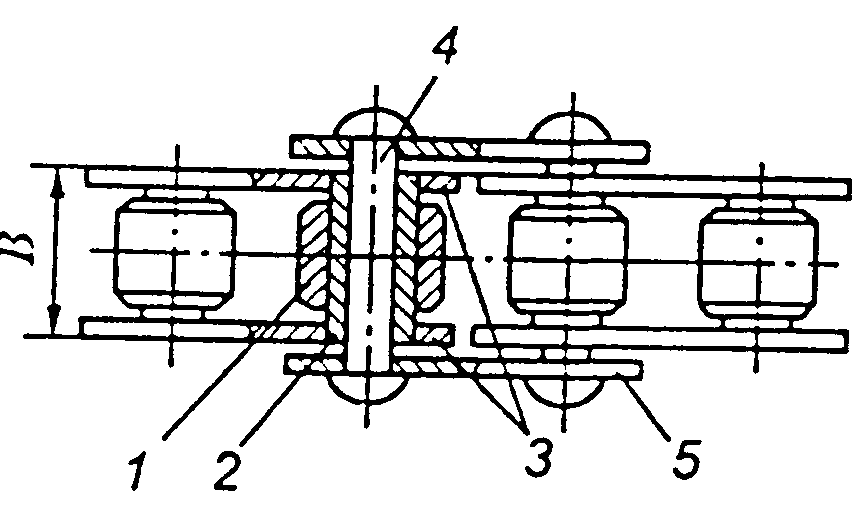
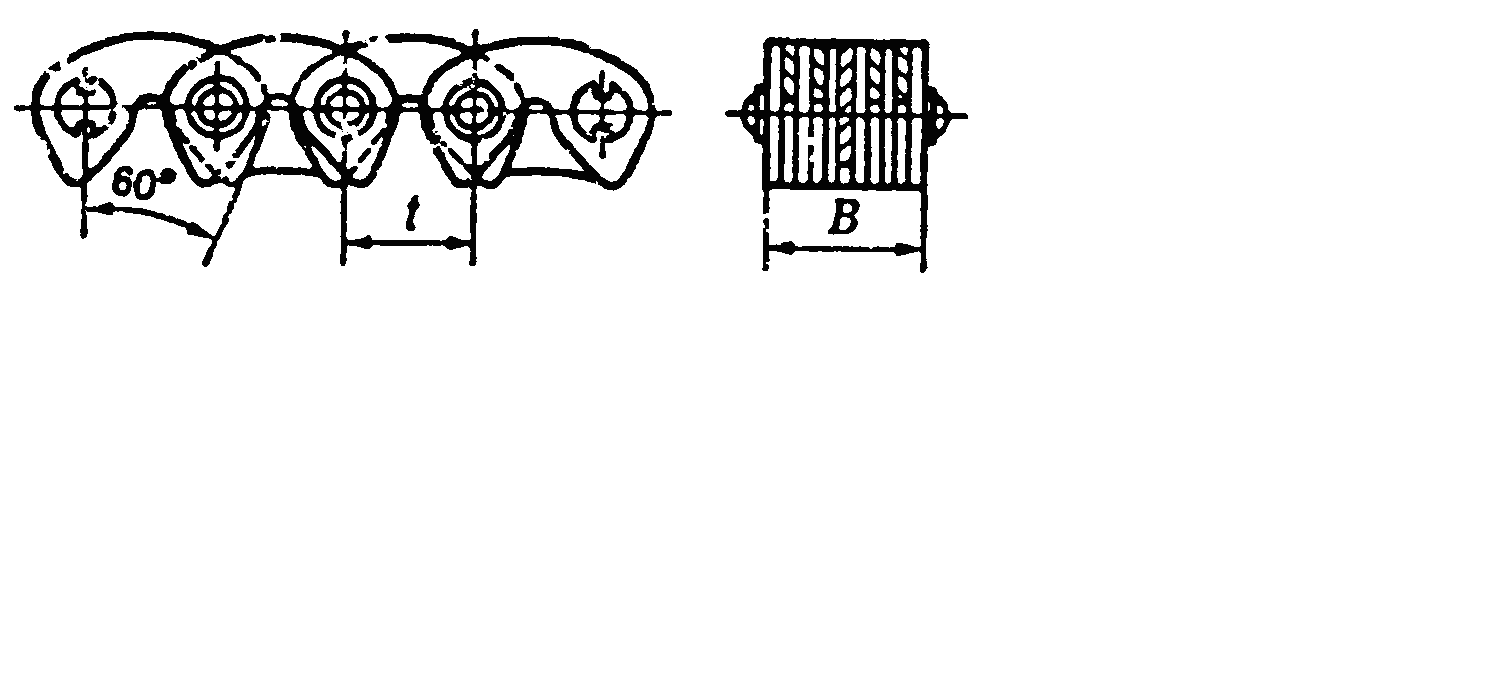
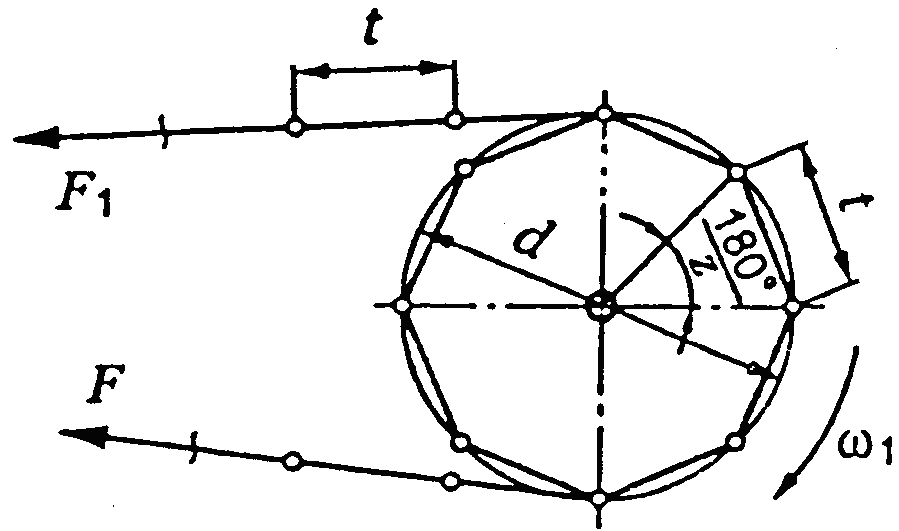
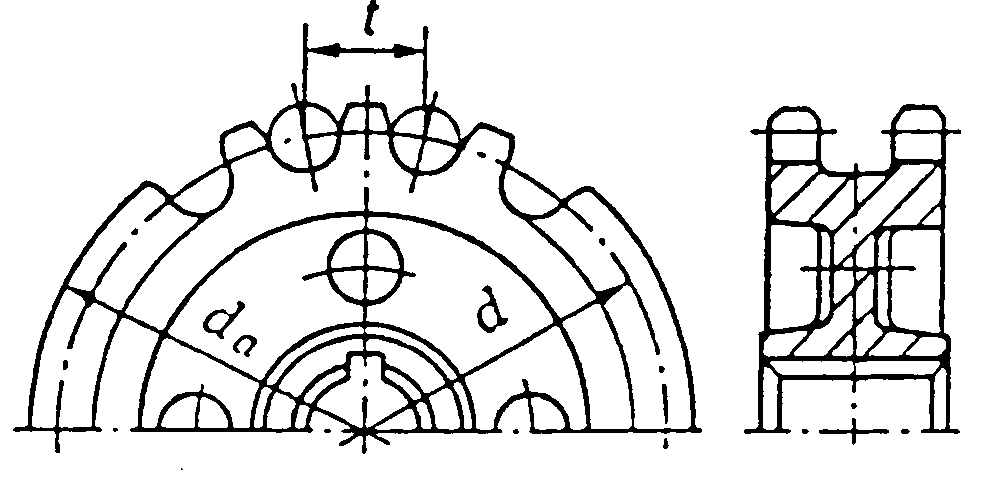
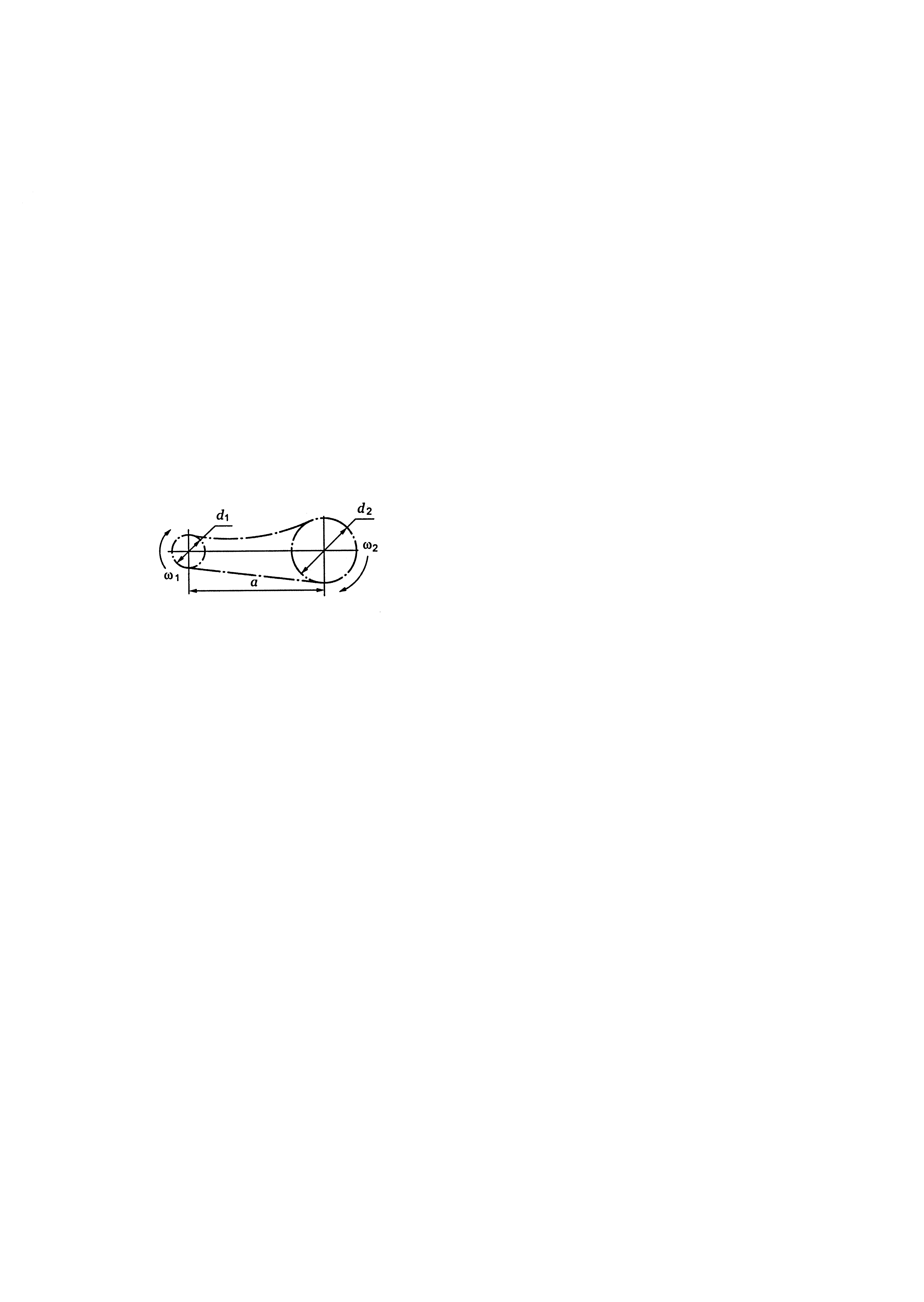
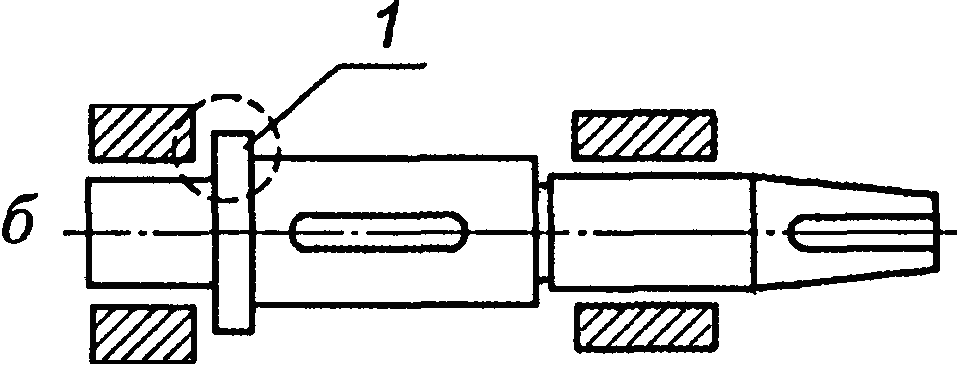
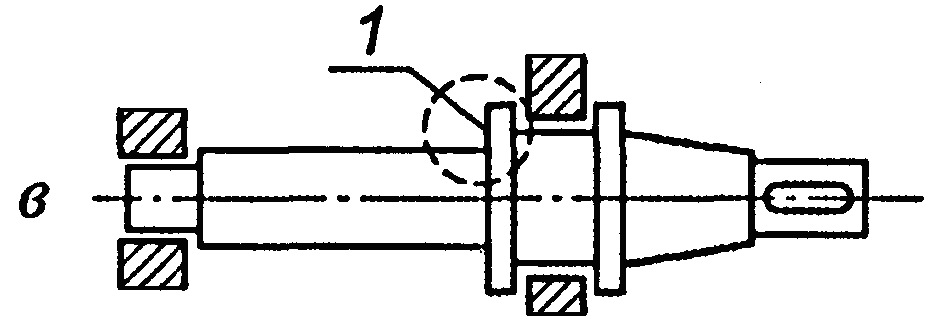
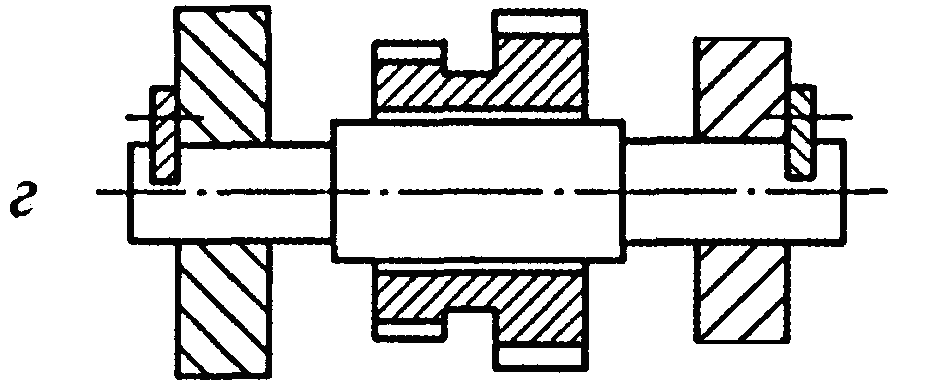
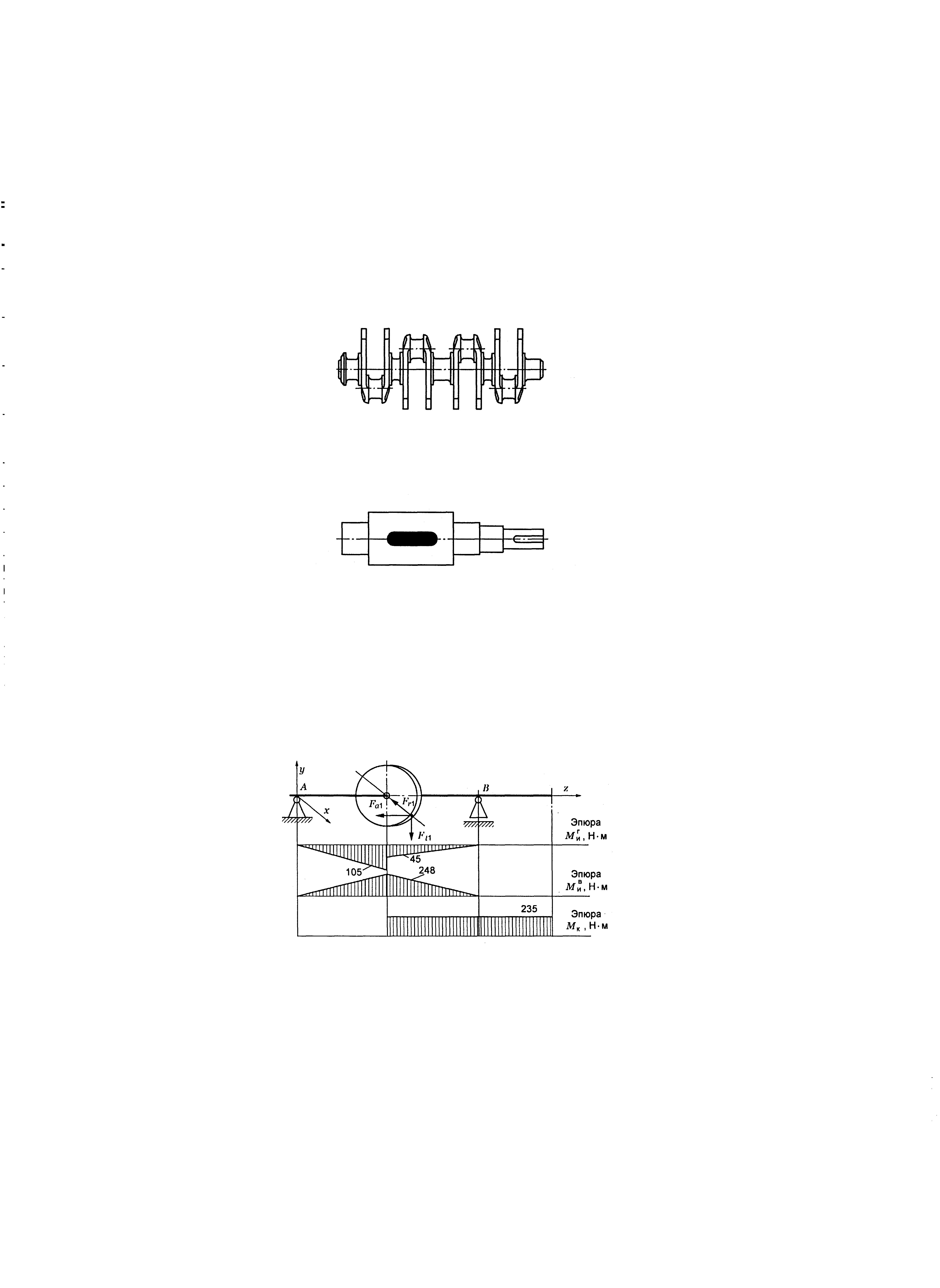

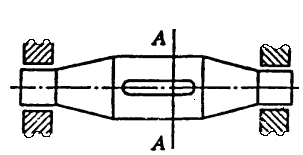
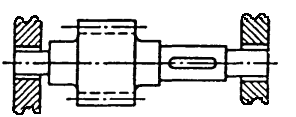
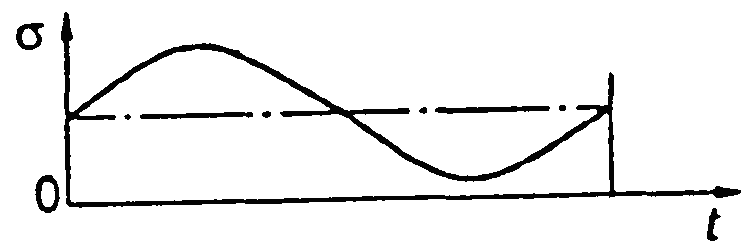

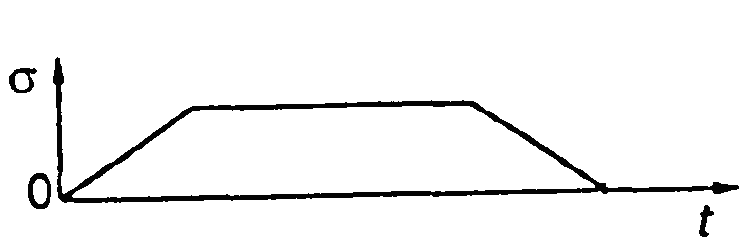
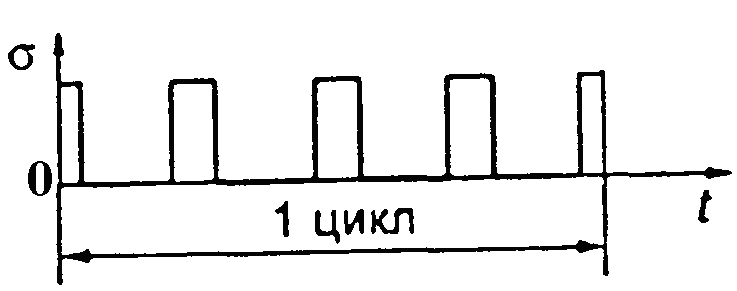
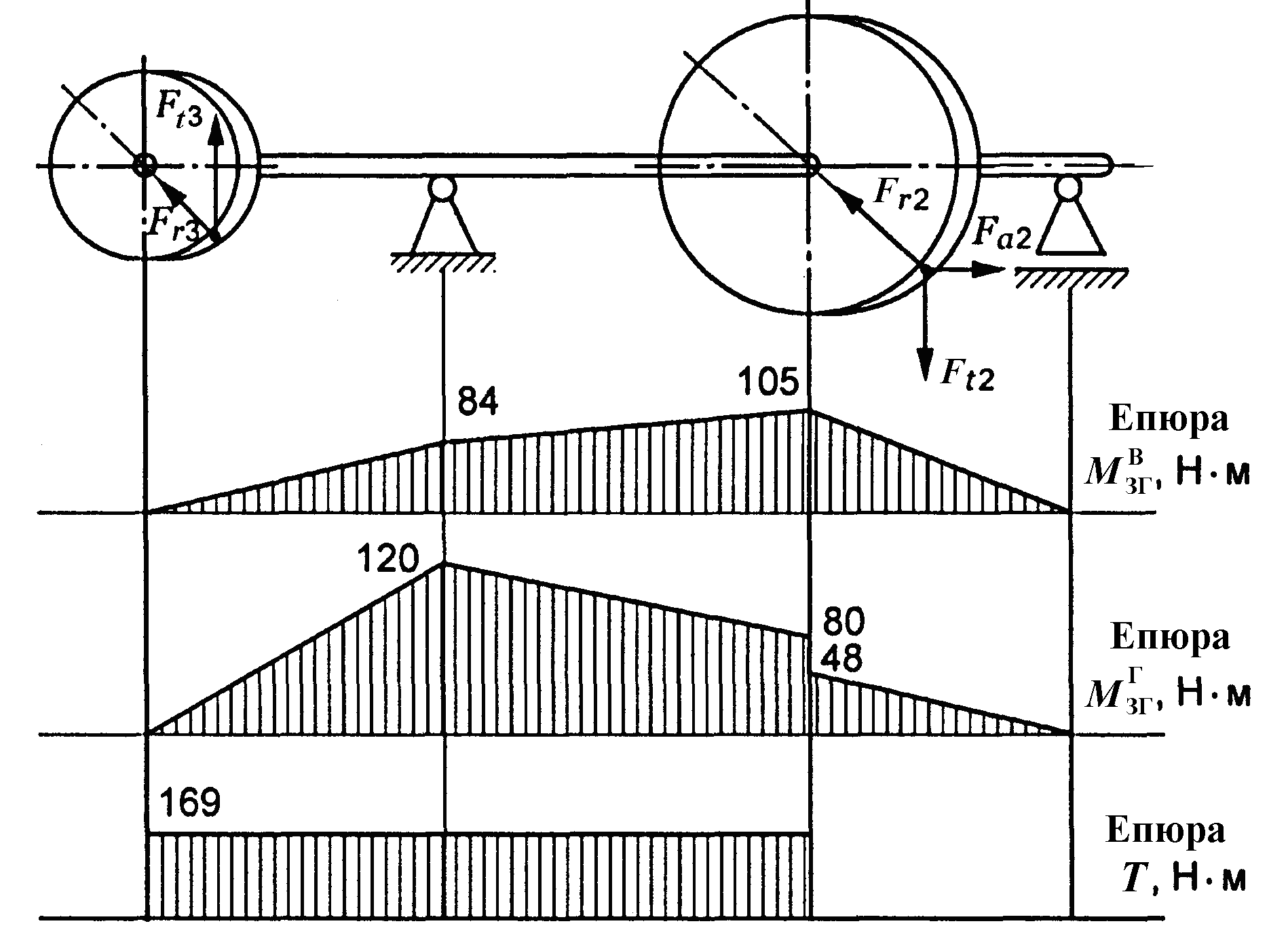
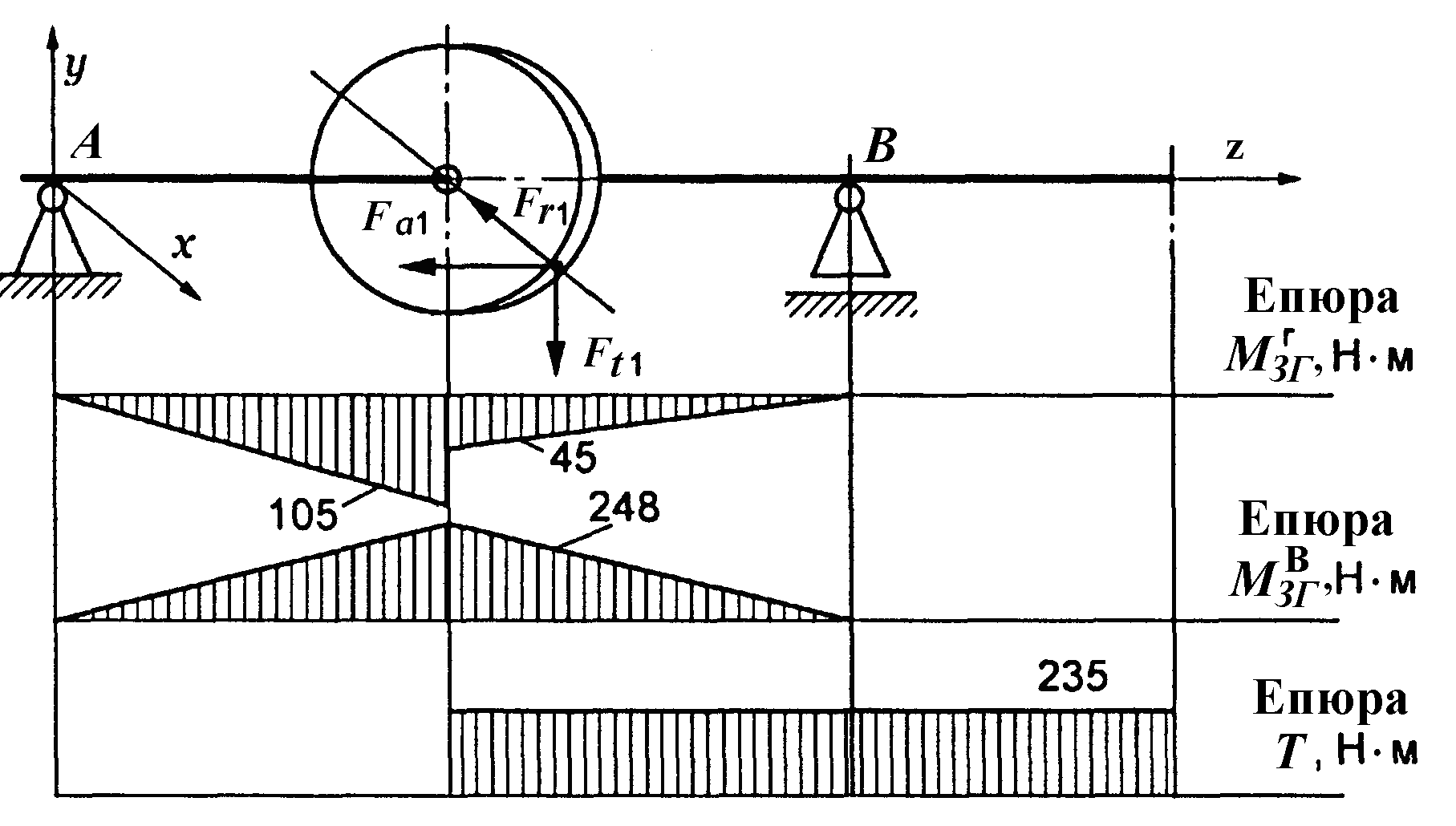
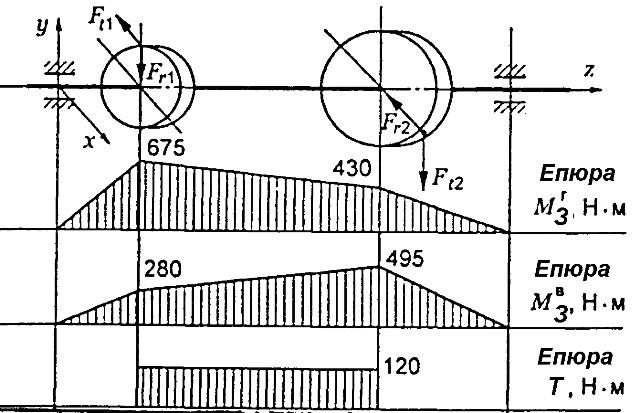
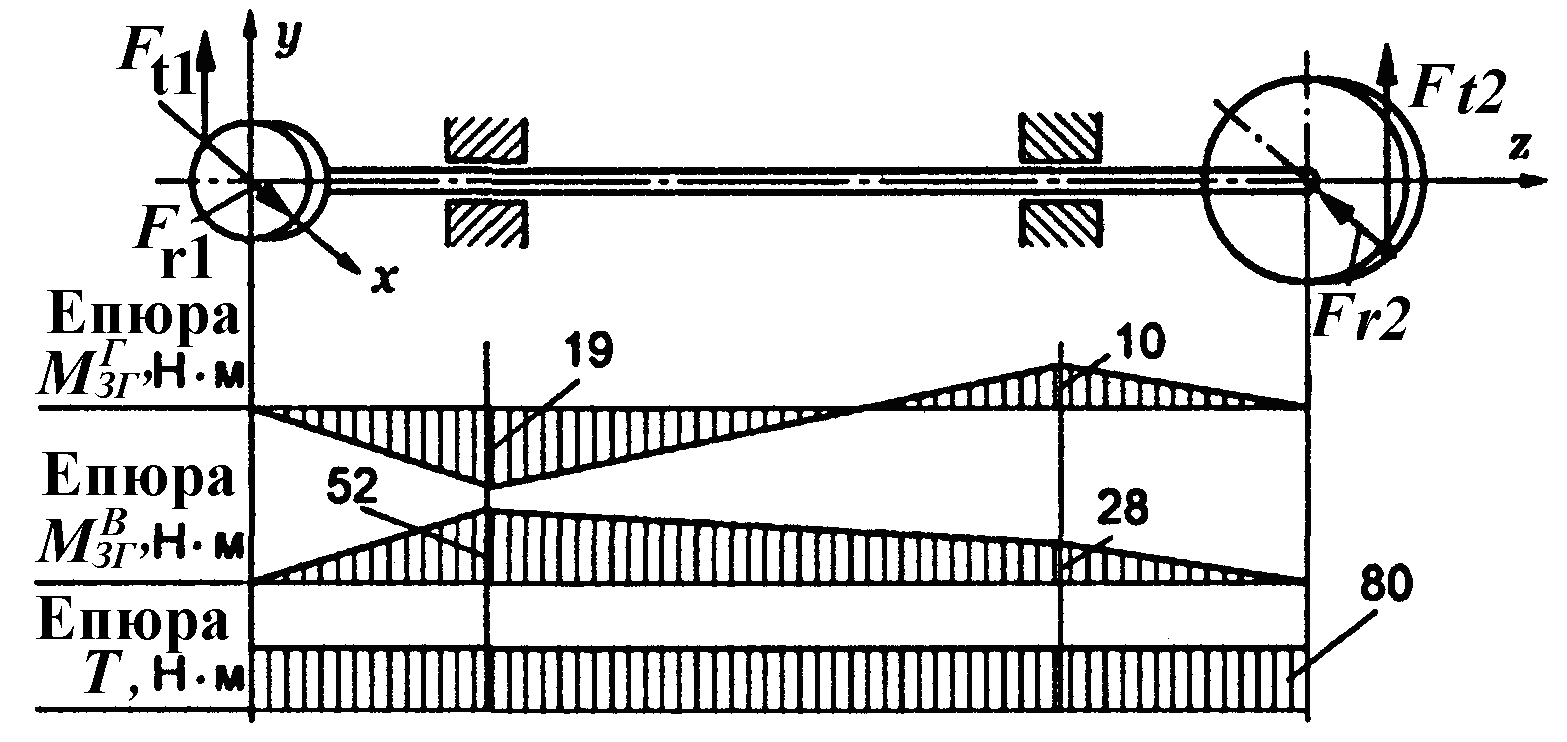
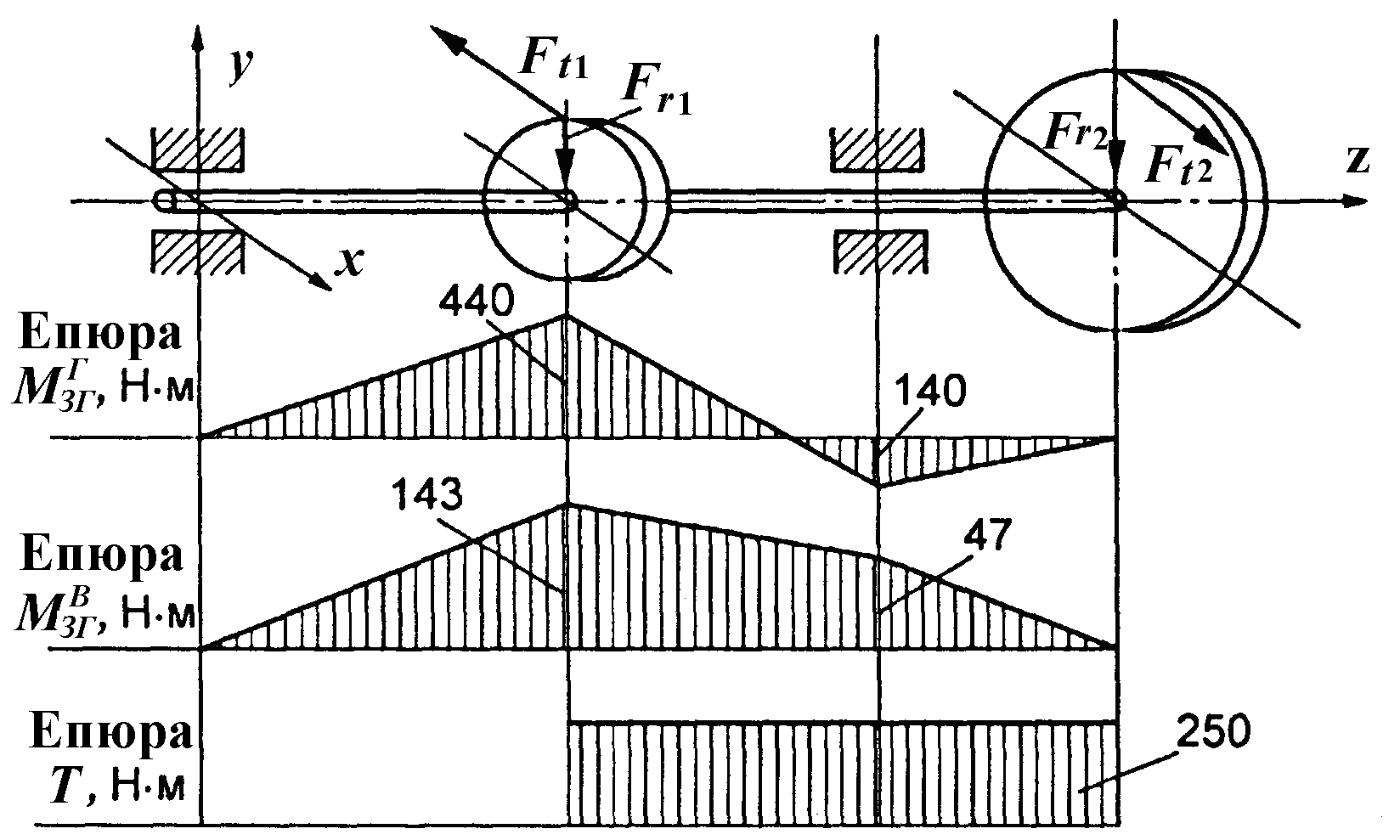
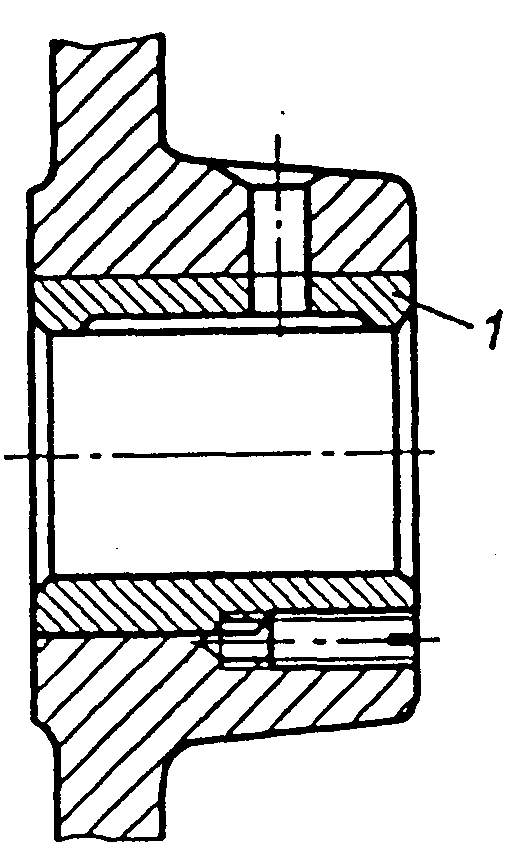
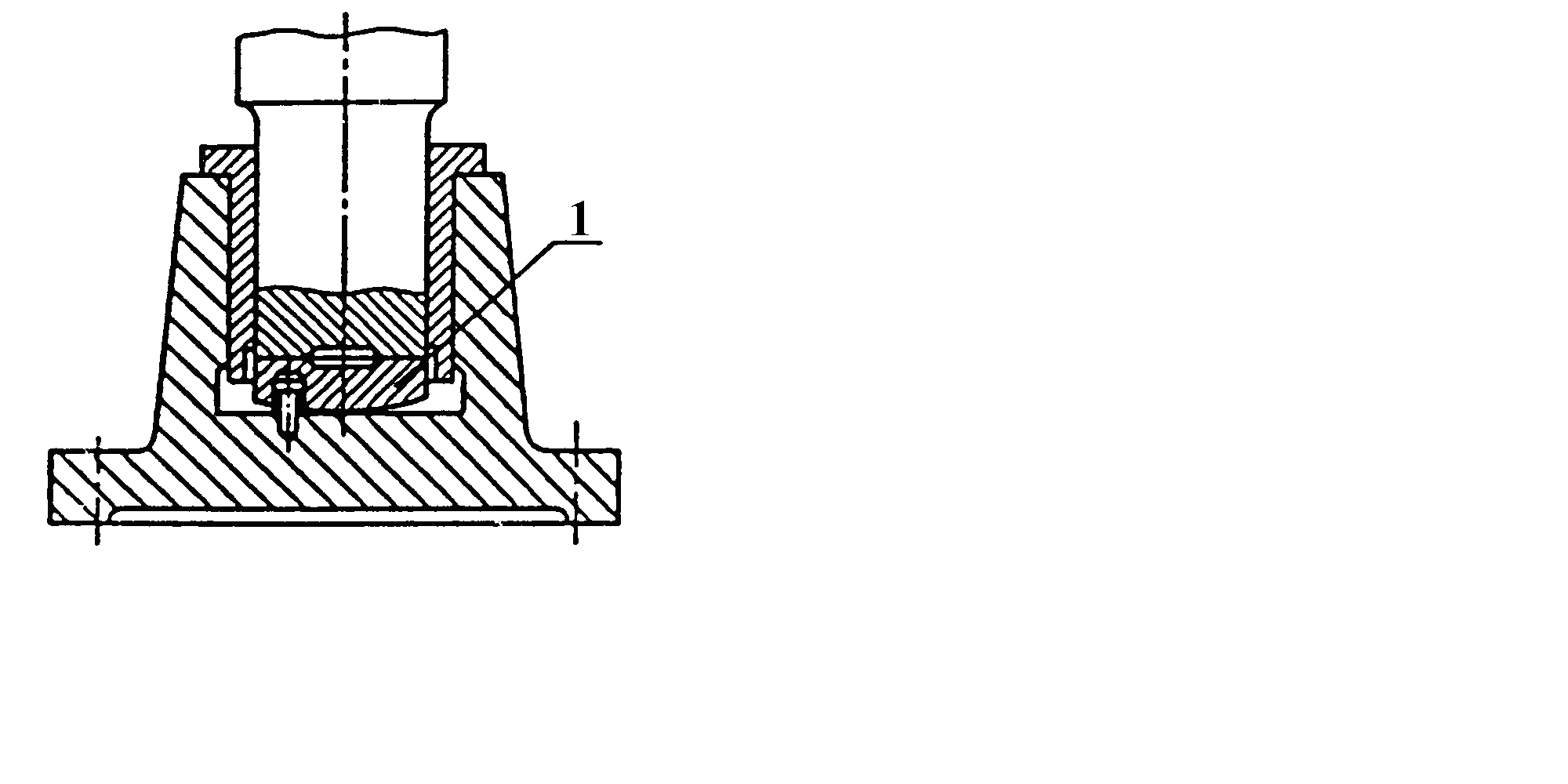
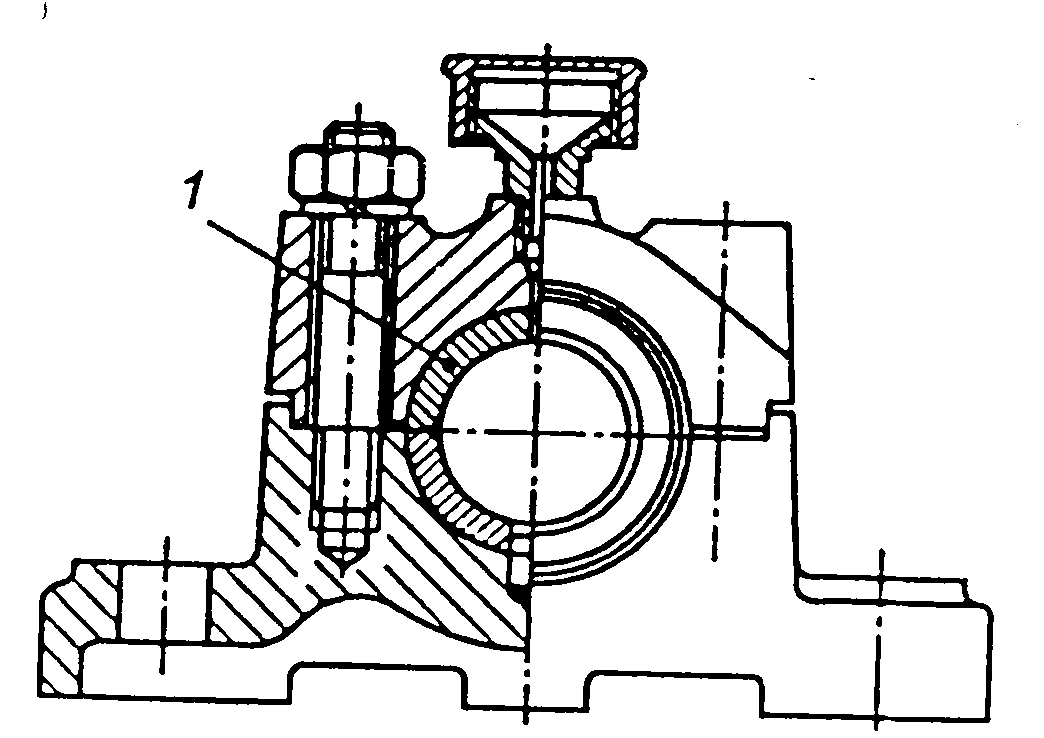
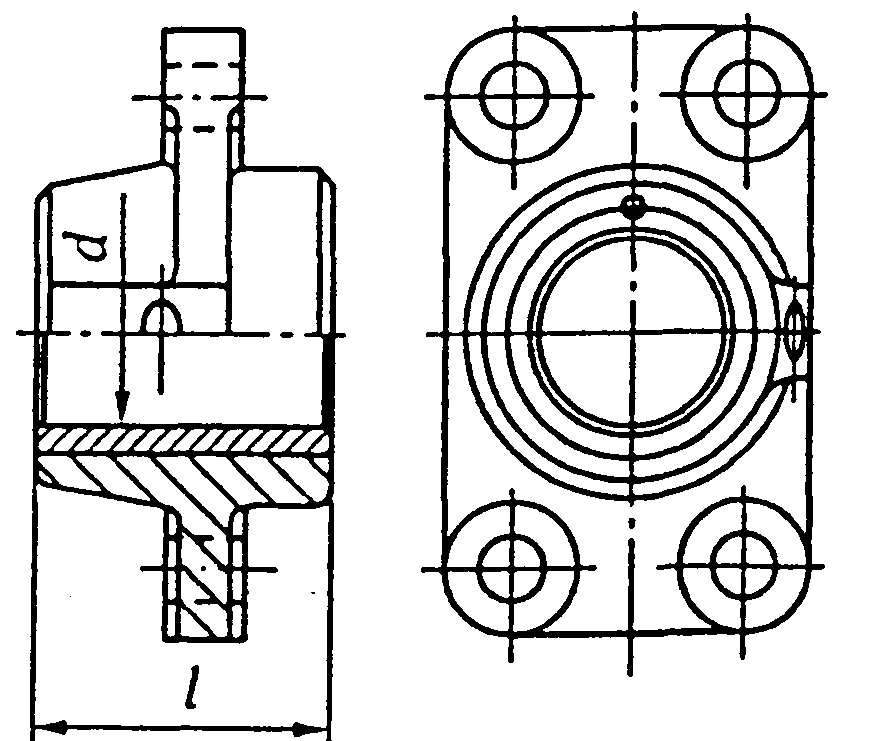

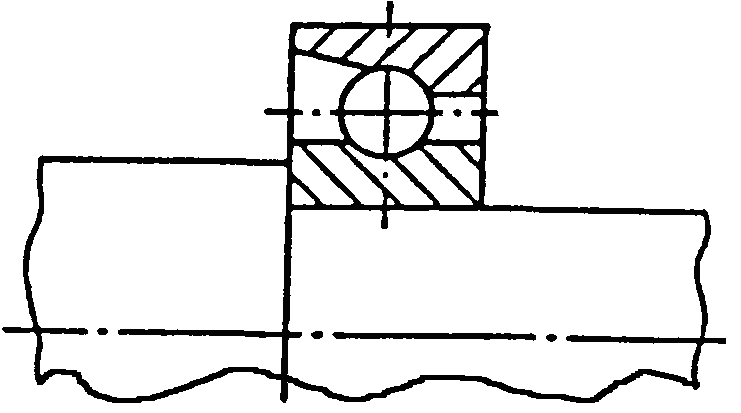
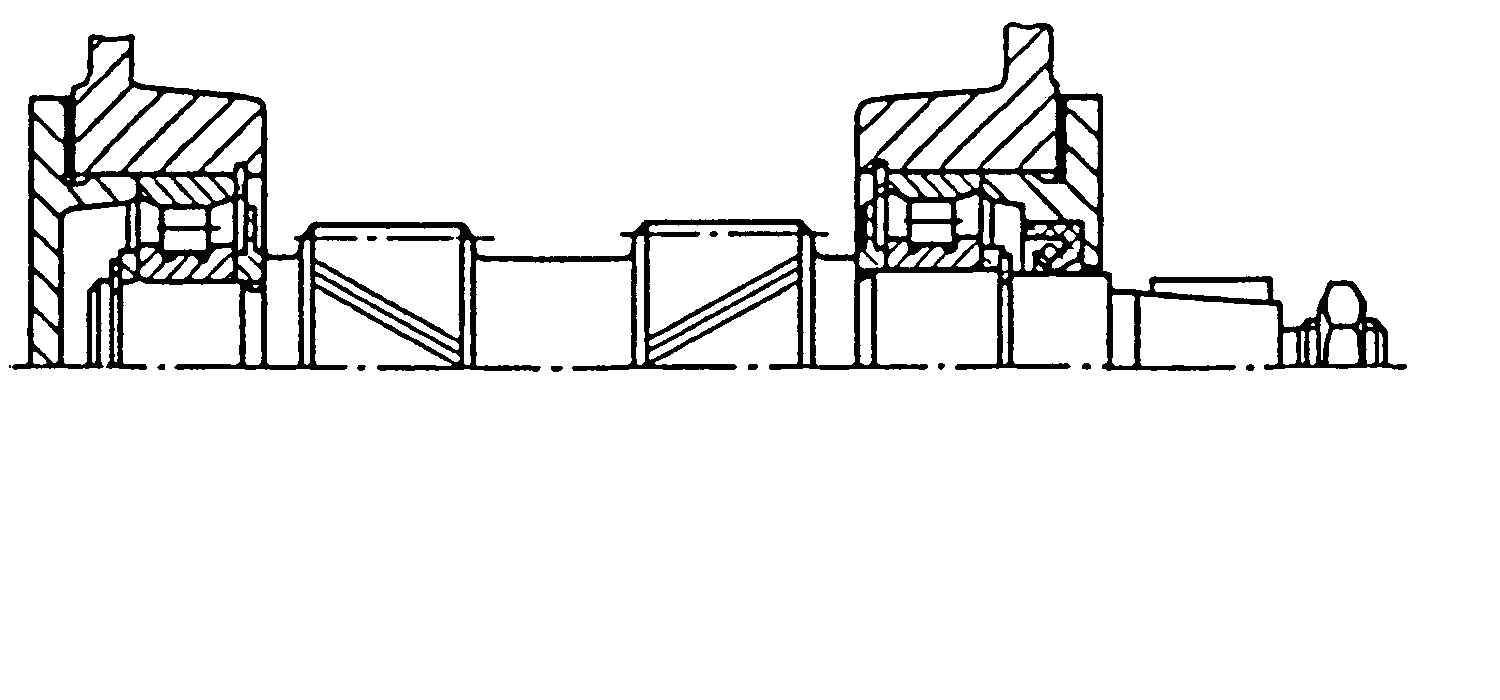
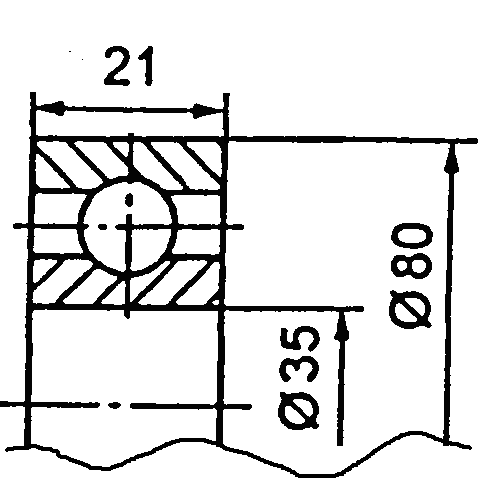
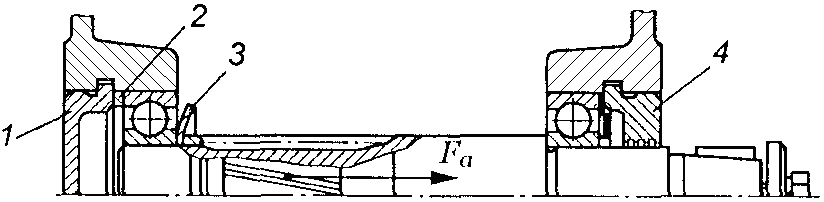
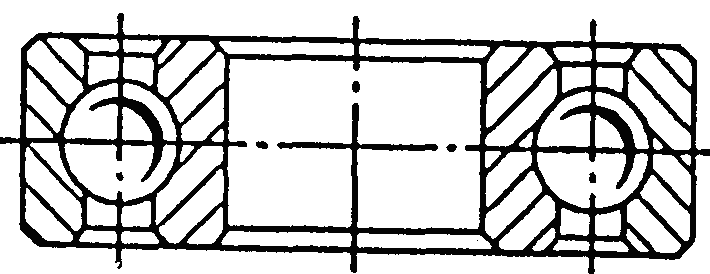
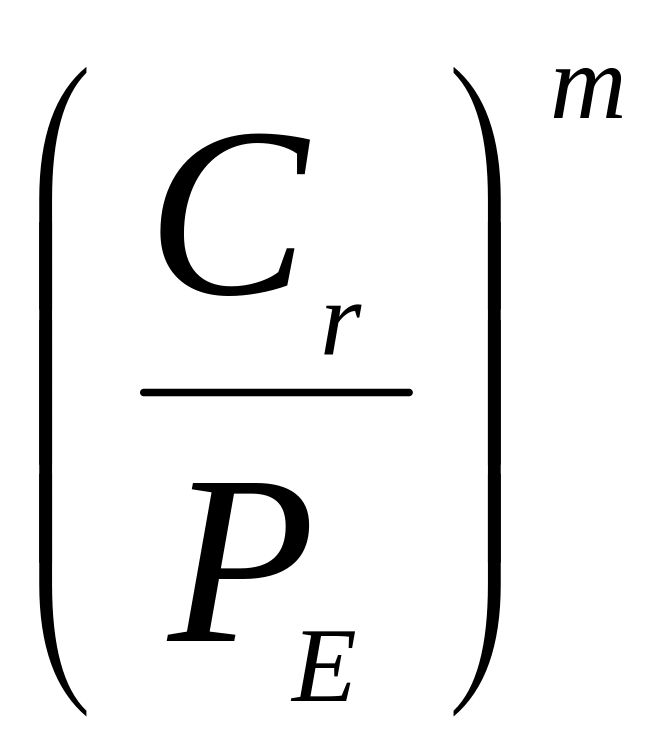 .
.