Кубічний інтерполяційний сплайн

Кубічні сплайн-функції моделюють дуже старий механічний пристрій, яким користувалися креслярі. Вони брали гнучкі рейки, виготовлені з досить пружного матеріалу, наприклад з дерева. Ці рейки закріплювали, підвішуючи важки в точках інтерполяції, що відповідають інтерполяційним вузлам. Рейка або механічний сплайн набирали форму з найменшою потенційною енергією. Остання умова має свій математичний вираз f^(IV)(x)  0. Якщо при цьому сплайн не руйнується, то тоді функція та її похідні повинні бути неперервними на [х₀,х_n] . З теорії балок відомо, що функція f(х) між кожною парою заданих точок може бути представлена поліномом 3-го степеня

f(x) = a_i + b_i(x - x_i) + c_i(x - x_i)² + d_i(x - x_i)³,

де х_i-1<х<х_i. При цьому між кожною парою сусідніх вузлів поліноми з'єднуються неперервно (так само, як їх перші та другі похідні).

Інтерполяція кубічними сплайнами - це швидкий, ефективний і стійкий спосіб інтерполяції функцій, що є основним конкурентом поліноміальної інтерполяції. У його основу покладена така ідея - інтервал інтерполяції розбивається на невеликі відрізки, на кожному з яких функція задається поліномом третього степеня. Коефіцієнти полінома підбираються так, що на границях інтервалів забезпечується неперервність функції, її першої та другої похідних. Також є можливість задати граничні умови - значення першої або другої похідних на границях інтервалу. Якщо значення однієї з похідних на границі відомі, то задавши їх, ми одержуємо вкрай точну інтерполяційну схему. Якщо значення невідомі, то можна задати другу похідну на границі, що дорівнює нулю, й одержати досить гарні результати.

Кубічну сплайн-функцію, що задовольняє умови f"(х₁)=f"(х_n)=0, називають природним кубічним сплайном. З математичної точки зору було доведено [Алберг, 1972], що вона є єдиною функцією з мінімальною кривизною серед усіх функцій, що інтерполюють функцію в заданих точках та мають квадратично інтегровану другу похідну. У цьому змісті кубічний сплайн буде самою гладкою функцією, що інтерполює задані точки.

Побудова кубічного сплайна - простий і чисельно стійкий процес. Для треба визначити 4 коефіцієнти для кожного проміжку , тобто 4n параметрів. Вимагається щоб у внутрішніх вузлах сплайн і його похідні до 2-го порядку були неперервними

, i=1,…,n-1; r=0,1,2.

Це дає 3n-3 умови для визначення параметрів, ще n+1 умова міститься у вимозі S₃(x_i) = y_i, i=0,1,…,n.. Разом маємо 4n-2 умови. Ще 2 умови, необхідні для однозначного визначення коефіцієнтів сплайна, як правило, задаються у вигляді граничних умов, тобто умов у точках a й b. Розглянемо природні граничні умови .

Позначивши та враховуючи її лінійність, одержуємо

, . (5.27)

Двічі інтегруючи (5.27), одержуємо

, (5.28)

, (5.29)

де А та B- постійні інтегрування. Вищезгадані умови дають

(5.30)

З них одержуємо

Підставляючи A та B в (5.29), одержуємо

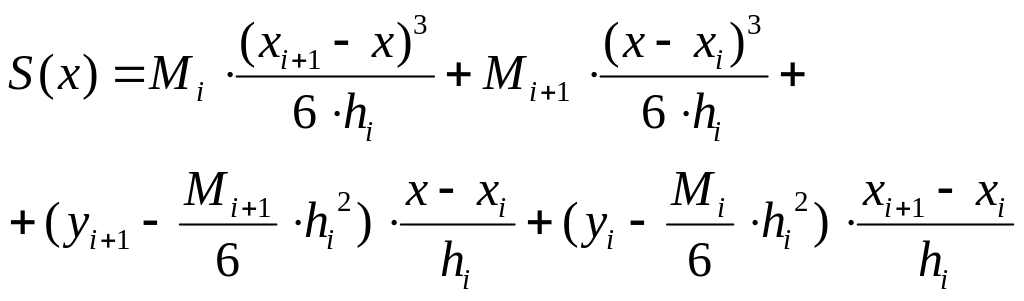(5.31)

. (5.32)

З (5.28) знаходимо значення однобічних похідних для вузла x_i, i=1,2,…,n-1

(5.33)

Вимагаючи неперервності у вузлі x_i одержуємо

, де i=1,…,n-1. (5.34)

Отже, отримуємо систему рівнянь відносно M_i вигляду

(5.35)

із квадратною матрицею A

і квадратною матрицею Н

.

Координатами вектора F є значення y₀,y₁,…,y_n.

Для матриці A ненульові елементи розміщені на головній діагоналі й двох сусідніх з нею. Такі матриці називаються тридіагональними. Для невиродженої матриці A виконана умова діагональної переваги . Отже, система (5.35) однозначно розв'язувана, тобто існує єдиний кубічний інтерполяційний сплайн.

Вигляд граничних умов змінює деякі елементи матриці A, але в кожному разі вона залишається матрицею з діагональною перевагою. Розв’язок системи (5.35) із тридіагональною матрицею A може бути знайдений методом прогонки.