
- •Розділ 5 Апроксимація функцій
- •5.1 Поняття про наближення функцій
- •5.2 Iнтерполювання функції
- •5.2.1 Інтерполювання за Лагранжем
- •1 Лінійна інтерполяція
- •2 Квадратична інтерполяція
- •5.2.2. Інтерполювання за Ньютоном
- •5.2.3 Інтерполювання за Ермітом
- •5.2.4 Похибка інтерполяції та способи її зменшення
- •5.2.5 Збіжність процесу інтерполяції
- •5.2.6 Інтерполяція за допомогою сплайнів
- •Лінійний інтерполяційний сплайн
- •Кубічний інтерполяційний сплайн
- •Випадки використання кубічного сплайна
- •Приклад реалізації алгоритмів інтерполяції функцій на псевдокоді
- •Апроксимаційні властивості кубічного сплайна
- •5.2.7 Застосування інтерполяції для складання таблиць
- •5.3 Метод найменших квадратів
- •Приклад реалізації методу найменших квадратів на псевдокоді.
- •Питання і завдання до розділу 5
2 Квадратична інтерполяція
У цьому випадку є три вузли
інтерполяції (![]() ).
Інтерполяційний поліном Лагранжа
набирає вигляду:
).
Інтерполяційний поліном Лагранжа
набирає вигляду:
 (5.7)
(5.7)
5.2.2. Інтерполювання за Ньютоном
Недоліком інтерполювання за Лагранжем є те, що якщо для поліпшення наближення додати ще один вузол інтерполювання, доведеться всі обчислення проводити заново.
На практиці часто трапляються випадки, коли вузли інтерполяції стають відомими не одразу, а поступово, один за одним, наприклад, у процесі вимірювання. Тоді зручно побудувати процес інтерполювання у такий спосіб, щоб поява даних про новий вузол інтерполювання, призводила б до необхідності мінімального перерахунку попередніх обчислень. Саме таку властивість має інтерполювання за Ньютоном.
Нехай вузли інтерполяції рівновіддалені один від одного за аргументом, тобто виконується умова
![]() ; (
; (![]() ). (5.8)
). (5.8)
Різниці
![]() (5.9)
(5.9)
називають скінченними різницями першого порядку. Різниці сусідніх скінченних різниць першого порядку
![]() (5.10)
(5.10)
називають скінченними різницями другого порядку. Аналогічно
![]() (5.11)
(5.11)
є скінченними різницями
![]() -го
порядку. Вони
визначаються за формулою
-го
порядку. Вони
визначаються за формулою
![]() де
де
![]() -біноміальні
коефіцієнти.
-біноміальні
коефіцієнти.
Розглянемо поліном
![]() .
(5.12)
.
(5.12)
Визначимо його коефіцієнти.
Коефіцієнт
![]() визначимо з умови проходження полінома
через першу точку (
визначимо з умови проходження полінома
через першу точку (![]() )
)
![]() . (5.13)
. (5.13)
З умови проходження полінома
через точку (![]() )
одержимо значення
)
одержимо значення
![]()
![]() ;
;![]()
![]() .
(5.14)
.
(5.14)
Аналогічно визначається решта коефіцієнтів
![]() . (5.15)
. (5.15)
Підставляючи отримані вирази у (5.12), одержуємо
![]() . (5.16)
. (5.16)
Це є перша інтерполяційна формула Ньютона (формула інтерполювання вперед).
Як бачимо, особливостями інтерполювання за Ньютоном є:
при появі нового вузла додається лише новий член, решта не перераховується;
коефіцієнти швидко зменшуються зі зростанням , бо у знаменнику міститься факторіал від .
Іноді використовується формула для інтерполювання назад
![]() .
.
Візьмемо деяку функцію f(x)![]() R
і систему вузлів інтерполяції
R
і систему вузлів інтерполяції
![]() ,
,
![]() ,
,
![]() при і
при і![]() j.
Вузли інтерполяції не є рівновіддаленими.
Для цієї функції і вузлів утворимо
відношення
j.
Вузли інтерполяції не є рівновіддаленими.
Для цієї функції і вузлів утворимо
відношення
![]()
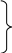
![]() .
.
 Вони
називаються розділеними
різницями першого порядку.
Одержавши
їх, ми можемо утворити
нові відношення
Вони
називаються розділеними
різницями першого порядку.
Одержавши
їх, ми можемо утворити
нові відношення
![]()
![]() …,
…,![]()
Вони називаються розділеними
різницями другого порядку.
Взагалі, якщо ми уже визначили розділені
різниці k-го
порядку
![]() ,то
розділені
різниці (k+1)-го порядку
знаходяться
за допомогою формули
,то
розділені
різниці (k+1)-го порядку
знаходяться
за допомогою формули
![]() .
.
Іноді замість
для позначення розділених різниць
використовують позначення
![]() .
.
Домовимося розміщувати таблиці розділених різниць у такий спосіб:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При
![]()
![]() скінченні і розділені різниці пов'язані
співвідношенням у вигляді
скінченні і розділені різниці пов'язані
співвідношенням у вигляді
![]()
Розділені різниці порядку n від многочлена n-го степеня постійні, а різниці більш високого порядку дорівнюють нулю. Останнім зауваженням можна скористатися для виявлення помилок у таблицях многочленів чи функцій, близьких до них.
За допомогою розділених різниць можна побудувати інтерполяційний многочлен Ньютона
![]()
![]()
Варто зазначити, що при збільшенні кількості вузлів процес обчислення скінченних та поділених різниць стає все більш обчислювально нестійким - похибка визначення скінченних різниць великого порядку різко зростає зі збільшенням порядку скінченної різниці. Тому метод Ньютона може бути застосований лише для невеликої кількості вузлів.
