20

Тема 7 Коэффициент корреляции Пирсона

Исследователей часто интересует, как связаны между собой две переменные в данной группе лиц (классы, школы, нации и т.д.). Например, имеют ли ученики, научившиеся читать раньше других, тенденцию к более высокой успеваемости в шестом классе? Наблюдаются ли в больших классах мéньшие успехи в приобретении знаний за семестр, чем в небольших классах? Связана ли средняя продолжительность работы педагогов в школе непосредственно со средней заработной платой? Очевидно, для ответа на такие вопросы мы должны провести наблюдения по каждой переменной для группы объектов (типичных представителей, которыми могут быть классы, школы, районы и т.д.). Данные, собранные для ответа на один из подобных вопросов, могут выглядеть, как в приведенной ниже таблице 7.1.

Таблица 7.1

№ учащегося	Оценка IQ (Х) Стенфорда – Бине	Необработанная оценка теста успеваемости по химии (Y)
1 2 3 4 5 6 7 8 9 10 11 12	120 112 110 120 103 126 113 114 106 108 128 109	31 25 19 24 17 28 18 20 16 15 27 19

В этом примере переменными, которые изучались у 12 школьников, были оценки IQ, определённые с помощью Шкалы интеллекта Стенфорда – Бине в шестом классе, и успеваемость по химии в средней школе, оцененная на основе теста, состоящего из 35 вопросов.

Связь между двумя переменными можно выразить графически диаграммой рассеивания. Диаграмма рассеивания для данных примера показана на рисунке 7.1.

На диаграмме рассеивания каждый ученик изображается точкой. Точка, или метка, располагается в месте пересечения прямых линий, проведенных через оценку IQ перпендикулярно оси Х и через оценку теста по химии перпендикулярно оси Y для каждого ученика. Диаграмма на рисунке 7.1 показывает слабую положительную связь Х и Y. Однако мы пока не имеем обобщенной меры этой связи.

Надо поставить общий вопрос о более точном смысле термина «связь». Существует ли соответствие большого значения Х большим или малым значениям тех же объектов по Y или систематического распределения по парам с большими и малыми значениями не наблюдается?

Положение объекта относительно остальных в выборке по Х и Y, определяемое средними двух распределений, проявляется в величинах и знаках отклонений и соответственно. Если объект имеет высокий уровень по обеим переменным, как, например, учащийся 11 в вышеприведенном примере, то произведение · будет большим и положительным. Аналогично, если он относительно низок как по Х, так и по Y, то для него также будет большим и положительным (поскольку произведение двух отрицательных чисел положительно).

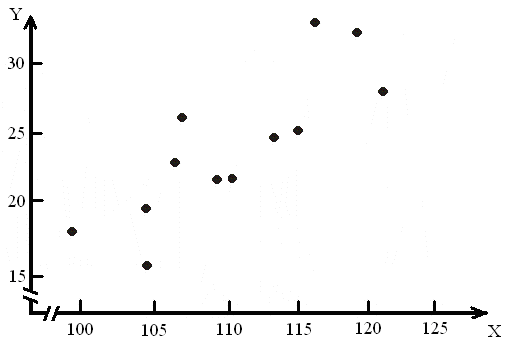
Рис. 7.1 – Диаграмма рассеивания, показывающая связь IQ (Х) с успеваемостью по химии (Y) для 12 школьников

Если Х и Y в основном связаны прямо (большие значения с большими, а малые – с малыми), то большинство произведений будет положительным: следовательно, сумма этих произведений для всех объектов [то есть ] будет большой и положительной.

Если Х и Y имеют обратную связь (большое Х встречается с малым Y и наоборот), то многие объекты с положительными значениями будут тяготеть к отрицательным значениям , а отрицательные – к положительным . В этом случае произведения будут, как правило, отрицательными. Следовательно,

будет отрицательной, когда Х и Y связаны обратной зависимостью.

Если Х и Y не имеют систематической связи (большие Х сочетаются с малыми Y столь же часто, как и с большими Y, и то же самое справедливо для малых Х), то среди объектов с большими положительными значениями у некоторых будут положительные, а у других – отрицательные. При образовании произведений одни сомножители станут положительными, а другие – отрицательными. Сумма произведений

должна приблизительно балансировать положительные и отрицательные члены и поэтому должна быть довольно близкой к нулю.

Таким образом, мы имеем величину , которая велика и положительна, когда Х и Y сильно связаны прямой зависимостью, близка к нулю в случае отсутствия связи между Х и Y и велика и отрицательна, когда Х и Y сильно связаны обратной зависимостью. Однако эта сумма произведений отклонений всё ещё не является адекватной обобщенной мерой связи. Прежде всего, её величина зависит от числа пар значений, участвующих в подсчёте. Так как мы можем пожелать сравнить степень связи между Х и Y в двух выборках разного объёма, то надо уметь измерять связь независимо от объёма групп. Простое усреднение позволяет достигнуть этого. Два средних значения для выборок разного объема сравниваются в терминах центров группирования данных, а простые суммы для двух выборок не сопоставляются. Вот почему мы берём среднее, если хотим, чтобы статистика не зависела от объёма выборки. Однако, по той же причине, по которой получилась в результате деления суммы квадратов отклонений на n – 1, а не на n, нам следует разделить

на n – 1.

Величина является мерой связи Х и Y и называется ковариацией Х и Y. Ковариация Х и Y обозначается через :

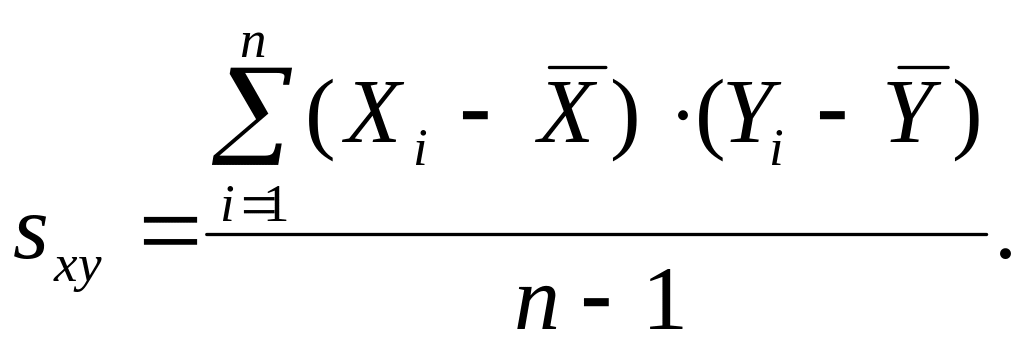(7.1)

Заметим, что ковариация Х с самим собой – это просто дисперсия Х:

Ковариация является вполне удовлетворительной мерой связи во многих задачах физики и техники. (Действительно, физики называют пресловутый бихевиористский «коэффициент корреляции», который часто встречается в зарубежных дидактических и психологических исследованиях, «безразмерной ковариацией»). И она представляет собой адекватную меру в той же степени, в какой шкала (среднее и дисперсия) переменных не является произвольной и имеет некоторый смысл. Многие переменные, с которыми мы имеем дело, измеряются в произвольных шкалах: среднее и дисперсию можно сделать любыми, какими вздумается, поскольку нас обычно интересует только взаимоположение объектов в группе. Это, в частности, верно для обработки психологических и педагогических данных.

Вычитание значений Х и Y из соответствующих средних сделало независимым от средних. Чтобы избавить меру связи от влияния стандартных отклонений двух групп значений, надо только разделить на и . В результате получим искомую меру связи Х и Y. Она называется коэффициентом корреляции – произведением моментов – Пирсона и обозначается :

. (7.2)

Обозначение r происходит от слова регрессия. На первоначальном этапе применения этого коэффициента Фрэнсисом Гальтоном и Карлом Пирсоном (1857–1936) он играл важную роль в исследовании связей физических характеристик людей, исследовании, которое вначале было направлено на изучение регрессии физических изменений от одного поколения к другому.