3. Линейное программирование

3.4. Симплексный метод с искусственным базисом (м-метод)

При решении задач линейного программирования симплексным методом иногда бывает достаточно сложно найти исходное опорное решение (в задачах, ограничения которых заданы неравенствами типа «≥» или равенствами). В этом случае применяют метод искусственного базиса (М-метод), который позволяет избежать затруднений, связанных с нахождением исходного опорного решения.

Алгоритм метода искусственного базиса

Шаг 1. Привести задачу линейного программирования к каноническому виду.

Шаг 2. Построить М-задачу. Для этого в каждое уравнение системы ограничений, не имеющее естественную базисную переменную, необходимо ввести искусственную переменную с коэффициентом 1, не меняя знак равенства. Искусственные переменные также вводятся и в целевую функцию с коэффициентом М (если решается задача на максимум) или +М (если решается задача на минимум), где М - сколь угодно большое число.

Шаг 3. Выписать исходное опорное решение.

Шаг 4. Заполнить первую симплексную таблицу. При применении к М-задаче симплекс-метода оценки _j теперь будут зависеть от «буквы М».

Шаг 5. Решить М-задачу симплексным методом. Критерий оптимальности проверяется по индексной строке так же, как и в обычном симплекс-методе. При сравнения оценок нужно помнить, что М - достаточно большое положительное число, поэтому из базиса в первую очередь будут выводиться искусственные переменные.

Учесть следующие возможные случаи:

а) если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующее решение исходной задачи являет оптимальным;

б) если в оптимальном решении М-задачи хотя бы одна из искусственных переменных не равна 0, то исходная задача не имеет оптимального решения из-за несовместности системы ограничений;

в) если М-задача не имеет оптимального решения, то исходная задача также не имеет оптимального решения.

Если искусственная переменная выводится из базиса, то в дальнейших расчетах она не участвует, то есть соответствующий ей столбец не пересчитывается.

Шаг 6. Когда все искусственные переменные будут выведены из базиса, а в индексной строке _j не будет «буквы М», завершить решение задачи обычным симплексным методом.

Пример. Решить задачу линейного программирования:

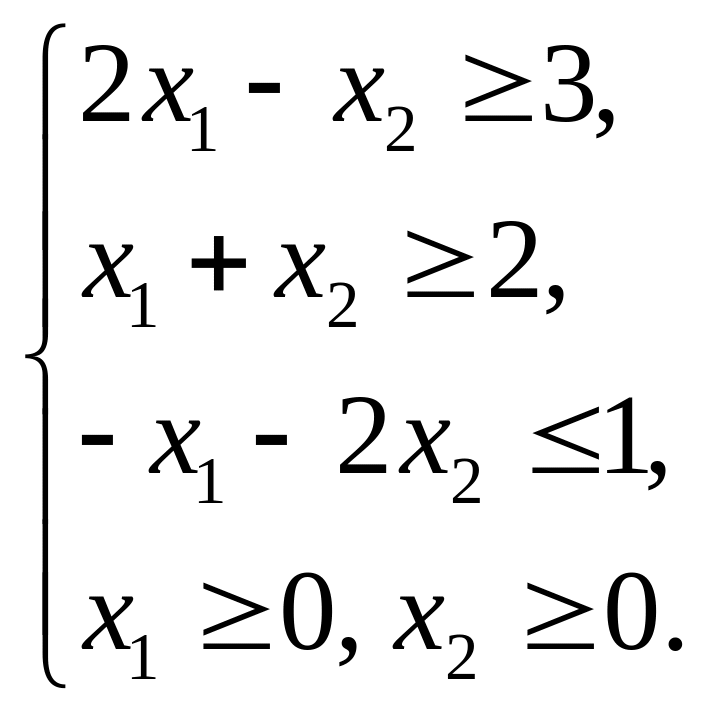
Приведем задачу к каноническому виду:

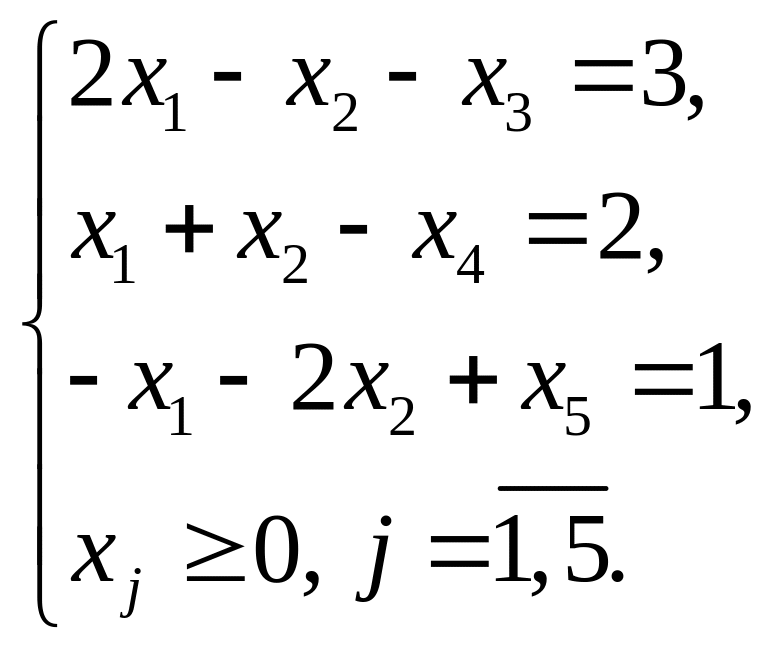
Для нахождения исходного опорного плана переходим к М-задаче:

В качестве базисных переменных возьмем z₁, z₂, х₅, тогда небазисные – х₁, х₂, х₃, х₄.

Полагаем х₁ = х₂= х₃= х₄= 0, тогда х₅ =1, z₁=3, z₂ =2.

1-я итерация.

Дальнейшее решение проводим в симплексных таблицах. Составляем первую симплексную таблицу, соответствующую исходному опорному решению (таблица 3.2):

.

Таблица 3.2

ci	БП	- 10	5	0	0	0	- M	- M	bi
		x1	x2	x3	x4	x5	z1	z2
- M	z1	2	- 1	- 1	0	0	1	0	3
- M	z2	1	1	0	- 1	0	0	1	2
0	x5	- 1	- 2	0	0	1	0	0	1
	j	-3M+10	- 5	M	M	0	0	0	- 5M

Все строки таблицы, за исключением индексной, заполняем по данным системы ограничений и целевой функции. Элементы последней строки рассчитываем:

,

и т.д.

В числе базисных переменных есть искусственные переменные, значит, найденное решение не является оптимальным и его можно улучшить. В качестве разрешающего столбца следует принять столбец переменной х₁:

, т.е. k =1.

За разрешающую строку принимаем строку переменной х₇:

, т.е. s =1.

Разрешающим является элемент а₁₁=2, т.е. вводим в базис переменную х₁, выводим z₁.

2-я итерация.

Формируем следующую симплексную таблицу (таблица 3.3).

ci	БП	- 10	5	0	0	0	- M	- M	bi
		x1	x2	x3	x4	x5	z1	z2
- 10	х1	1	-1/2	-1/2	0	0		0	3/2
- M	z2	0	3/2	1/2	-1	0		1	1/2
0	x5	0	-5/2	-1/2	0	1		0	5/2
	j	0	-3М/2	-М/2+5	М	0		0	-М/2-15

Из таблицы 3.3 находим опорный план:

.

В числе базисных переменных есть искусственные переменные, значит, найденное решение не является оптимальным и его можно улучшить. Разрешающим элементом является а₂₂=3/2.

3-я итерация.

Формируем следующую симплексную таблицу (таблица 3.4).

ci	БП	- 10	5	0	0	0	- M	- M	bi
		x1	x2	x3	x4	x5	z1	z2
- 10	х1	1	0	-1/3	-1/3	0			5/3
5	х2	0	1	1/3	-2/3	0			1/3
0	x5	0	0	0	-5/3	1			10/3
	j	0	0	5	0	0			-15

В третьей симплекс-таблице получен опорный план исходной задачи ЛП:

, .

Поскольку все оценки , то это решение является и оптимальным, т.е. х₁=5/3, х₂=1/3 (основные переменные), х₃=0, х₄=0, х₅=10/3 (дополнительные переменные), при этом