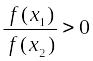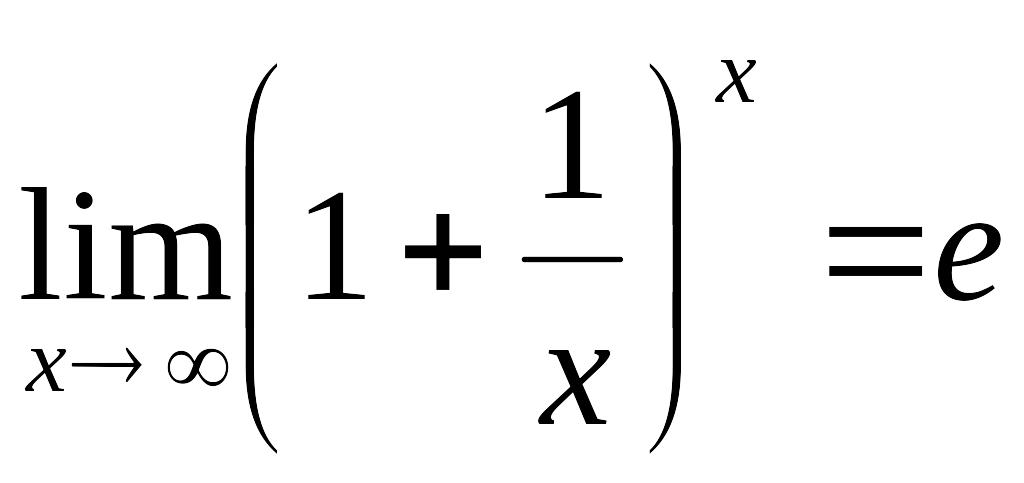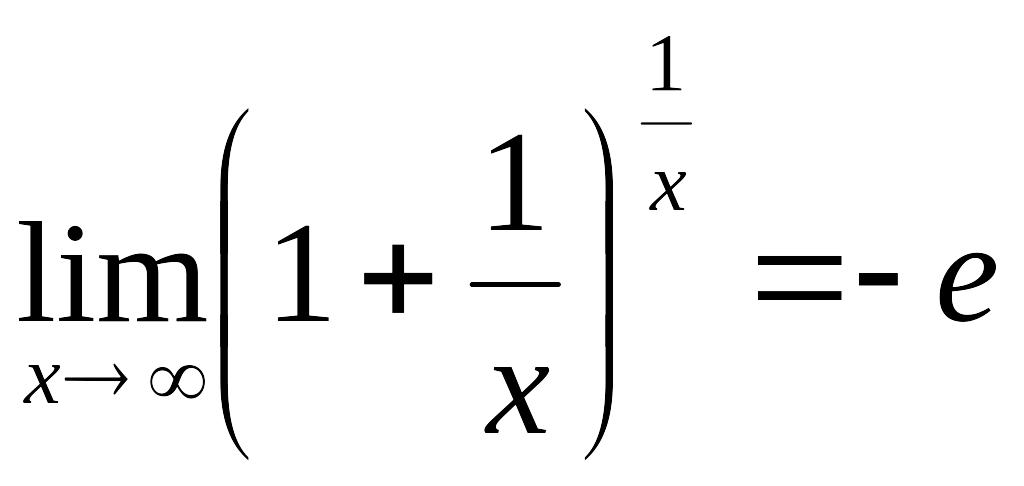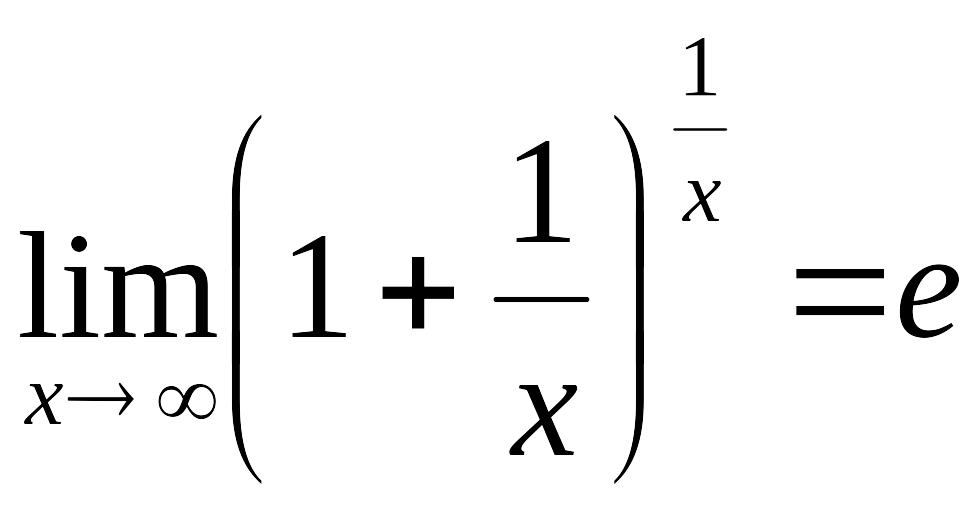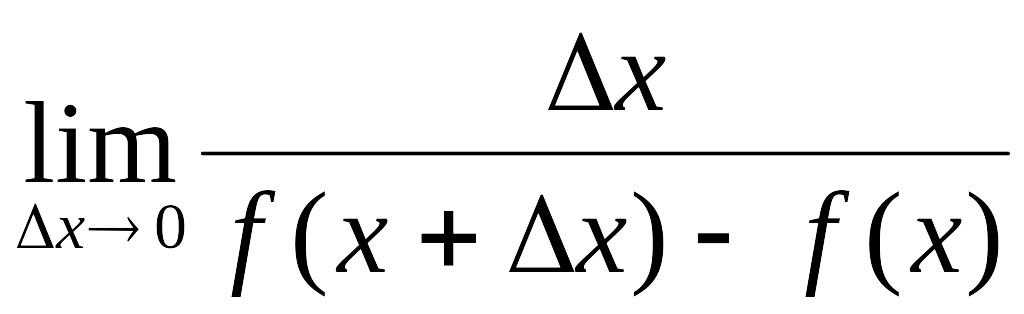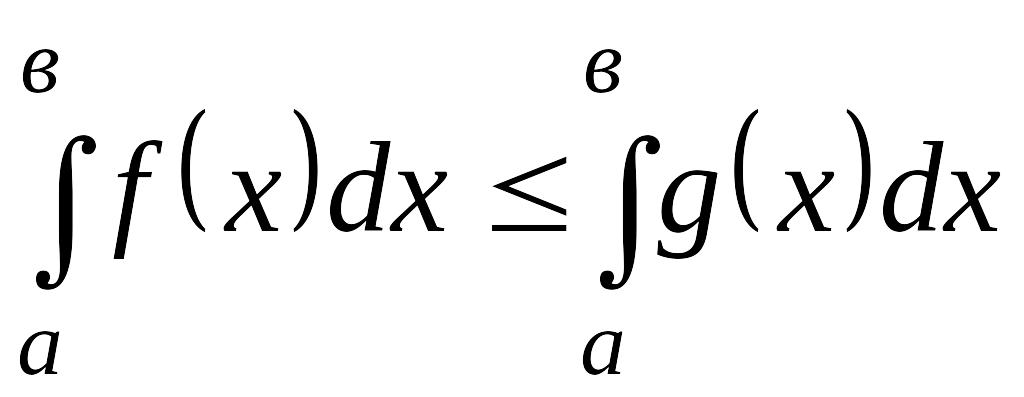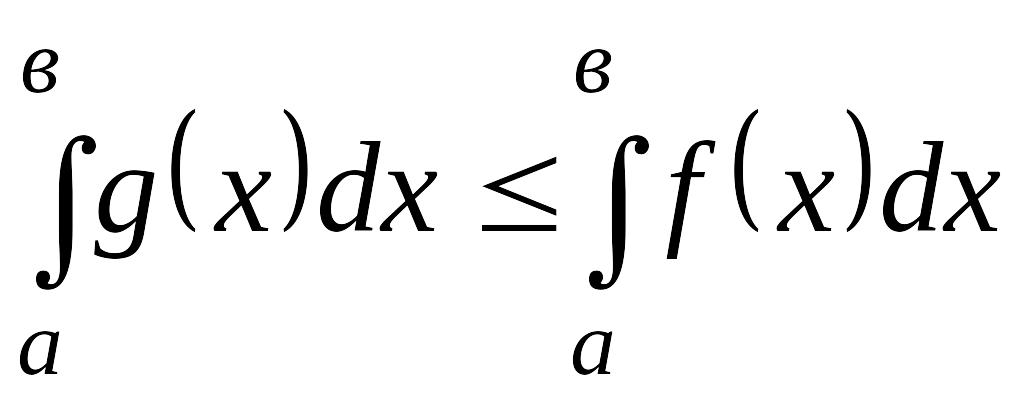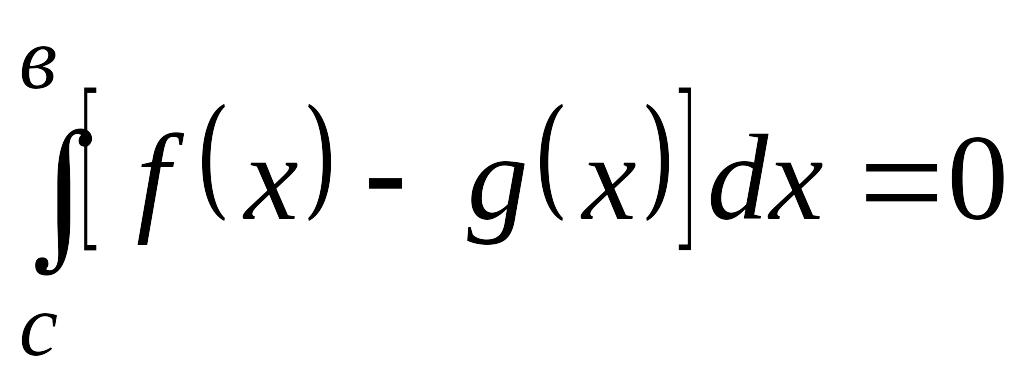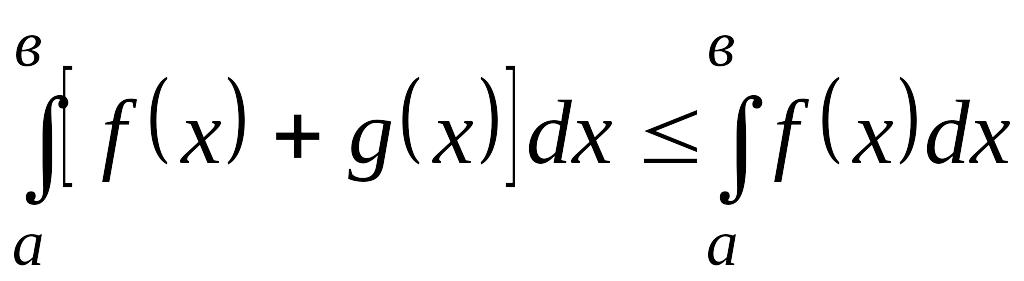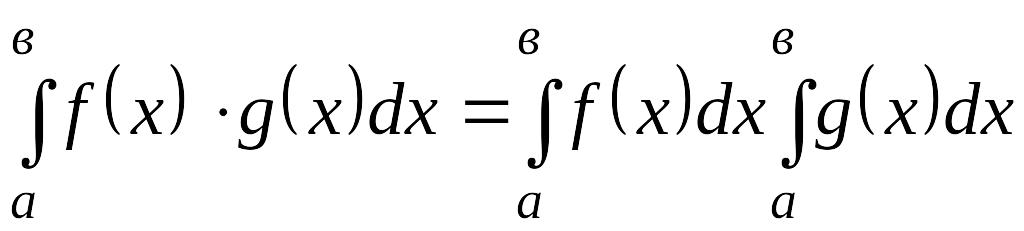1 Тарау

функциясы кесіндісінде үзіліссіз болса, онда кесіндісінде

1. шектелген

2. шектелмеген

3. периодты

4. тақ

5. анықталмаған

функциясы қандай да бір аралықта өспелі болуы үшін болғанда функцияның сәйкес мәндері қандай теңсіздікті қанағаттандыруы керек:

1. 

2. 

3. 

4. 

5. 

1-ші тамаша шекті көрсетіңіз:

1. 

2. 

3. 

4. 

5. 

2-ші тамаша шекті көрсетіңіз:

1. 

2. 

3. 

4. 

5. 

Егер нүктесінде функциясы үзіліссіз болмаса, онда нүктесі

1. функцияның үзіліс нүктесі

2. экстремум нүктесі

3. минимум нүктесі

4. максимум нүктесі

5. анықталу нүктесі

функциясы қандай да бір аралықта кемімелі болуы үшін болғанда функцияның сәйкес мәндері қандай теңсіздікті қанағаттандыруы керек:

ұмтылғанда функциясы қай функцияға эквивалент:

1. 

2. 

3. 

4. 

5. 

2 Тарау

функциясының нүктесіндегі жанамасының теңдеуі болса, онда туралы не айтуға болады:

1. 0-ге тең

2. шексіз туындысы бар

3. 1-ге тең

4. туындысы жоқ

5. -1-ге тең

функциясының туындысы қандай да бір интервалда теріс болса, онда функциясы осы интервалда:

1. 0-ге тең

2. өседі

3. тұрақты

4. үзілісті

5. кемиді

болсын. Онда функциясының туындысы:

1. 

2. 

3. 

4. 

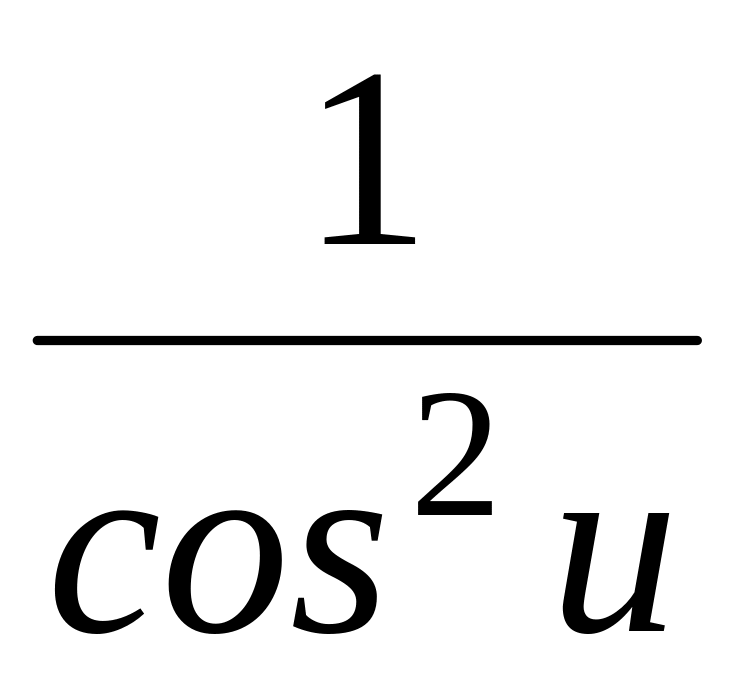
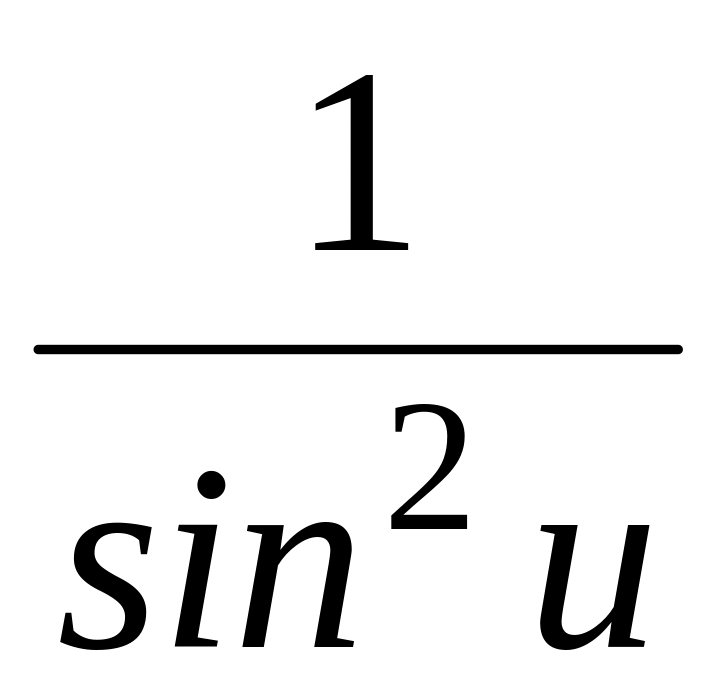
5. С

болсын. Онда функциясының туындысын тап:

1. 

2. 

3. 

4. 

5. 

функциясының нүктесіндегі туындысы деп белгіленеді және төмендегі формулалардың қайсысымен есептелінеді?

1. 

2. 

3. 

4. 

5. 

Дәрежелік функцияның туындысын есептейтін формуланы көрсет:

1. 

2. 

3. 

4. 

5. 

Көбейтіндінің туындысын есептеу ережесі

1. 

2. 

3. 

4. 

5. 

3 Тарау

функциясы аралығында функциясының алғашқы функциясы болса,онда

1. 

2. 

3. 

4. 

5. 

Дарбудың жоғарғы қосындысын көрсет:

1. 

2. 

3. +

4. 

5. 

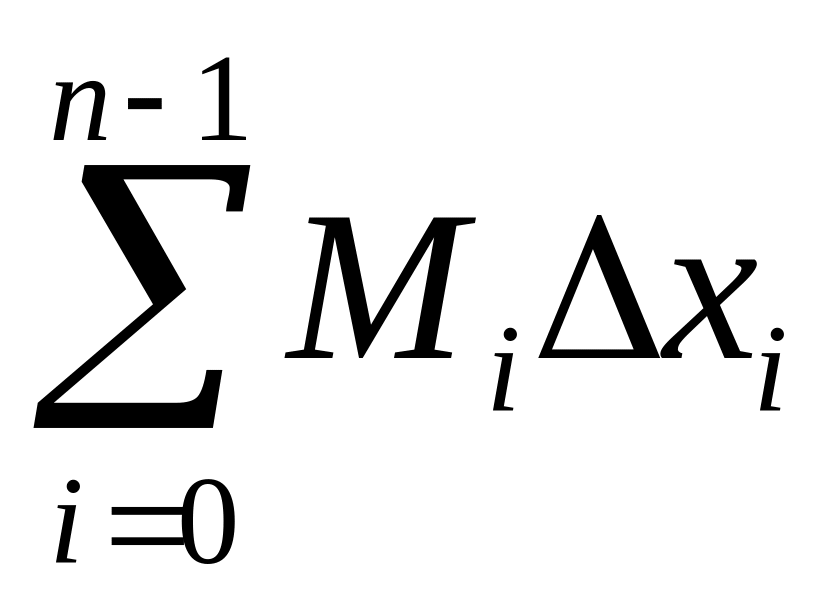
теңдеуімен берілген қисықтың аралығындағы доғасының ұзындығын есептеңіз:

1. 

2. 

3. 

4. 

5. 

қисығымен, ОХ осімен және түзулерімен шектелген фигураны ОУ осінен айналдырғанда пайда болған дененің көлемі неге тең:

1. 

2. 

3. 

4. 

5. 

Егер , -да интегралданатын болса және :f(x)≤ g(x) онда:

1. 

2. 

3. 

4. 

5. 

Дарбудың төменгі қосындысын көрсет:

3. +

5. 

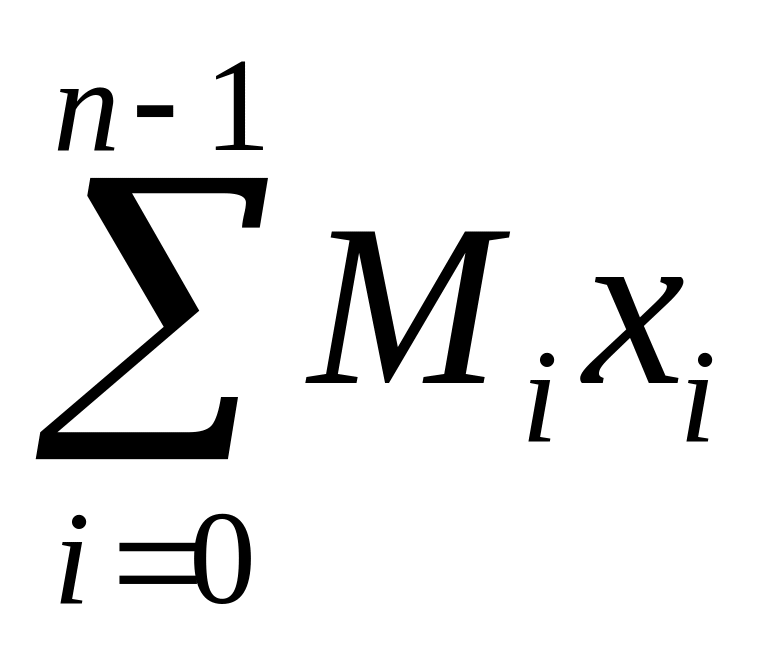
теңдеуімен берілген қисықтың аралығындағы доғасының ұзындығын есептеңіз:

1. 

2. 

3. 

4. 

5. 

4 Тарау

А={2, 3, 8, 9, 11} және В={3, 5, 8, 9, 13, 15} жиындары берілген. А/В жиынын табыңыз:

1. {2, 11}

2. {2, 8}

3. {13, 15}

4. {5, 11, 13, 15}

5. {11}

А={5, 8, 9, 13, 15} және В={7, 10, 13, 15} жиындары берілген. А/В жиынын табыңыз:

1. {5, 8, 9}

2. {5, 15}

3. {5, 10, 15}

4. {5, 11, 13, 15}

5. {11}

А=[0, 2] және В=(1, 3] жиындары берілген. Онда А В табыңыз:

1. (1,2]

2. Æ

3. [1,2)

4. [0,3]

5. [0,3]\{1}

және жиындары берілген. Онда табыңыз:

1. 

2. 

3. 

4. 

5. 

А={5, 8, 9, 11, 12, 15} және В={8, 9, 13, 15, 16, 20} жиындары берілген. Қиылысуын табыңыз:

1. {8, 9,15}

2. {5, 11}

3. {13, 15}

4. {5, 11, 13, 15}

5. {11}

А={5, 8, 9, 11} және В={7, 10, 13, 15, 25, 35, 37} жиындары берілген. Қиылысуын табыңыз:

1. 

2. {8, 9}

3. {13, 15}

4. {5, 11, 13, 15}

5. {11}

А={5, 8, 9, 10, 13, 15} және В={7, 10, 13, 15, 17} жиындары берілген. Қиылысуын табыңыз:

1. {10, 13, 15}

2. {8, 9}

3. {11, 1, 2}

4. {5, 11, 13, 15}

5. {11}