УПП3КУРС / спизжено / Сортировочные устройства

где hн, hк – энергетические высоты, соответствующие скорости движения отцепа в начальной и конечной точках участка скатывания, м эн. в.

Основное уравнение движения (формула (4.12)) вагона может быть выражено в энергетических высотах:

При этом скорость движения вагона (отцепа) в любой точке определяется по энергетической высоте:

соответственно скорость и кинетическая энергия тяжеловесных вагонов будет больше, чем легковесных.

С помощью основного уравнения движения вагона или отцепа решаются различные задачи по определению скорости, дальности пробега и других параметров скатывания вагонов с сортировочной горки.

Пример.

Задача 1. На сортировочный путь с уклоном 0,6 о/оо со скоростью 1,4 м/с выходит отцеп с удельным суммарным сопротивлением движению w = 4,7 кгс/тс, состоящий из

двух вагонов: четырехосный полувагон весом Q = 64 тс; восьмиосная платформа весом

Q = 70 тс. Определить дальность пробега отцепа в сортировочном парке.

Решение:

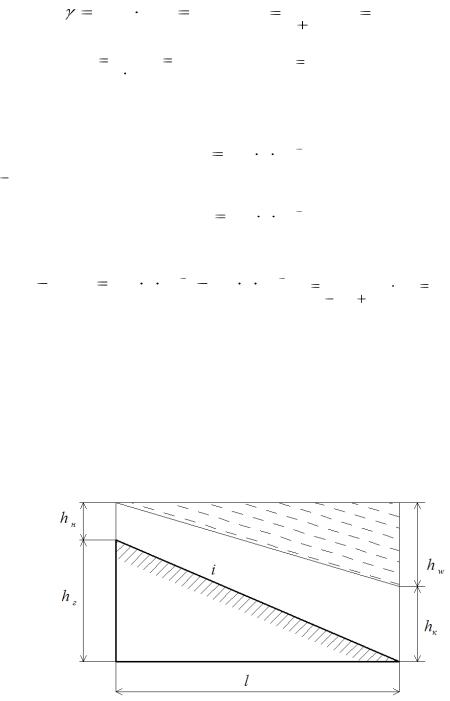
Составляется схема распределения энергетической высоты при скатывании вагона с горки

(рис. 4.3).

Рис. 4.3. Схема изменения энергетической высоты при скатывании вагона по расчетному участку

При этом энергетическая высота, соответствующая кинетической энергии отцепа в конечной точке участка скатывания будет равна нулю, так как отцеп должен остановиться

(vк = 0).

Используя формулы (4.8 – 4.17), определяются составляющие основного уравнения движения отцепа:

значения энергетической высоты, соответствующей кинетической энергии отцепа в начальной и конечной точках участка скатывания по формуле (4.14). Для этого необходимо рассчитать значение g' для заданного отцепа (формулы (4.8 – 4.9)):

значение энергетической высоты, соответствующей запасу потенциальной энергии отцепа в начале участка скатывания (профильной высоте участка) по формуле (4.15):

Составляется основное уравнение движения отцепа (формула 4.17), из которого можно выразить и найти значение l:

сопротивлением движению w = 2,2 кгс/тс. Определить скорость соударения с ближайшим вагоном, стоящим на сортировочном пути на расстоянии 98 м от начала участка скатывания.

Решение.

Составляется схема распределения энергетической высоты при скатывании вагона с горки (рис. 4.4).

Рис. 4.4. Схема изменения энергетической высоты при скатывании вагона по расчетному участку

Как и в предыдущей задаче, определяются составляющие основного уравнения движения отцепа:

значения энергетической высоты, соответствующие кинетической энергии отцепа в начальной и конечной точках участка скатывания, по формуле (4.14). Для этого необходимо рассчитать значение g' для заданного отцепа

(формулы (4.8 – 4.9)):

значение энергетической высоты, соответствующей запасу потенциальной энергии отцепа в начале участка скатывания (профильной высоте участка) по формуле (4.15):

значение энергетической высоты, потерянной при преодолении всех сил сопротивления движению на участке пути, по формуле (4.16):

Составляется основное уравнение движения отцепа, из которого можно выразить и найти значение vк:

Скорость соударения одиночного вагона с ближайшим вагоном, стоящим на сортировочном пути составит 1,47 м/с.

4.4. Силы сопротивления движению отцепа при скатывании с горки

4.4.1. Общая характеристика удельных сил сопротивления Запас энергетической высоты отцепа при скатывании с горки расходуется на

преодоление сил сопротивления скатыванию. При проектировании горок важно правильно определить суммарное воздействие сил сопротивления на скатывающийся отцеп, так как от этого зависят высота и профиль горки,

мощность тормозных средств и другие конструктивные параметры.

Силы сопротивления, действующие на отцеп при его скатывании с горки,

делят на две группы: управляемые и неуправляемые.

Управляемые силы сопротивления – удельное сопротивление,

возникающее при торможении на тормозных позициях wт (см. п. 8.3).

К неуправляемым силам сопротивления w относят:

основное удельное сопротивление wо;

удельное сопротивление от воздушной среды и ветра wсв,

удельное сопротивление от снега и инея wсн;

удельное сопротивление от стрелочных переводов и кривых wск

Каждая сила сопротивления – случайная величина, зависящая от множества факторов: параметров окружающей среды, характеристик отцепа, типа и состояния верхнего строения пути и др.

4.4.2. Основное удельное сопротивление движению отцепа

Основным называют сопротивление движению вагона на прямом горизонтальном участке пути, обусловленное трением деталей буксовых узлов, трением качения между колесами и рельсами, ударами на межрельсовых стыках, рассеиванием энергии на колебание балласта,

земляного полотна и т.п.

Основное удельное сопротивление wо зависит от следующих факторов:

веса вагона и осевой нагрузки;

состояния ходовых частей вагона;

температуры окружающей среды и буксового узла;

состояния верхнего и нижнего строения пути и поверхности рельсов.

Также отмечена зависимость величины wо от времени стоянки состава в парке приема перед расформированием (чем дольше простаивает состав, тем выше сопротивление вагонов при роспуске). Кроме того, отмечено увеличение основного сопротивления с понижением температуры воздуха до

– 25 ºС, при дальнейшем понижении температуры воздуха значение величины wо будет уменьшаться.

Величина wо является случайной, то есть у вагонов одного типа и массы может при одинаковых условиях принимать различные значения. Средние значения приведены в табл. 4.2, /2/.

Таблица 4.2

Средние значения основного удельного сопротивления движению вагона

Гистограммы распределений основного сопротивления wо хорошо согласуются с законом, соответствующим гамма-распределению (рис. 4.5),

/12/.

Рис. 4.5. Кривая функции плотности вероятности f(wо) распределения основного удельного сопротивления для всех весовых категорий вагонов

Из графика функции плотности вероятности f(wо) для всех весовых категорий

(рис. 4.5) видно, что с повышением весовой категории вагонов функция

плотности вероятности становится более узкой и островершинной. Разброс значений удельного сопротивления с повышением весовой категории вагона уменьшается, а также уменьшается и среднее значение. Это значит, что

тяжеловесные вагоны имеют меньшее основное сопротивление движению,

и, следовательно, лучшую динамику скатывания.

Расчет удельной работы сил основного сопротивления производится по формуле, м эн. в.:

где wо – среднее значение основного удельного сопротивления движению вагона, кгс/тс; l р – длина расчетного маршрута, м.

4.4.3. Удельное сопротивление движению отцепа от воздушной среды и ветра

Сопротивление от воздушной среды и ветра может принимать, как положительные, так и отрицательные значения, и соответственно, может способствовать как замедлению, так и разгону скатывающегося отцепа.

Удельное сопротивление от среды и ветра wсв зависит от следующих факторов:

температуры наружного воздуха;

скорости и направления ветра в период скатывания отцепа;

веса и скорости движения отцепа;

числа вагонов в отцепе;

площади поверхности отцепа, на которую воздействует давление воздушного потока.

Основным фактором, оказывающим наибольшее влияние на значение этого вида сопротивления, является ветер. Встречный ветер увеличивает сопротивление, а попутный – уменьшает его. Боковой ветер, дующий под углом 15 – 30к направлению оси путей, действует не только на торцевую,

но и на боковую поверхность вагона и оказывает более значительное воздействие, чем встречный или попутный ветер.

Особенно значительно действие ветра сказывается на движении легковесных отцепов.

Расчет удельного сопротивления движению вагона от воздушной среды и ветра wсв (кгс/тс) ведется по формулам:

для отцепов из нескольких вагонов:

(273 tн ) Q

1

для одиночных вагонов:

где cx – коэффициент воздушного сопротивления одиночных вагонов или первого вагона в отцепе; cxxj – коэффициент воздушного сопротивления вагонов в отцепе (кроме первого вагона); S, Si – площадь поперечного сечения (мидель) соответственно одиночного (или первого) вагона в отцепе и последующих вагонов в отцепе, м2; Q – вес вагона, тс; vот – относительная скорость скатывания отцепа с учетом направления ветра, м/с; tн –

температура наружного воздуха, оС.

Коэффициенты cx и cxx принимаются по табл. 4.3 в зависимости от рода вагона и угла α между результирующим вектором относительной скорости vот и направлением движения отцепа (рис. 4.6), /2/.

б) При встречном ветре

Рис. 4.6. Схема определения вектора относительной скорости скатывания vот,

углов и

Знак «+» в формуле (4.23) принимается при встречном ветре, знак «–» – при попутном. При скорости попутного ветра больше скорости отцепа wсв

принимается со знаком «–».

Угол α между результирующим вектором относительной скорости vлт и

направлением движения отцепа определяется по формуле:

Расчет удельной работы сил сопротивления от среды и ветра выполняется по формуле (м эн. в.):

где p – количество расчетных участков горки.

4.4.4. Удельное сопротивление движению отцепа от стрелочных переводов и кривых

Сопротивление движению от кривых (включая кривые стрелочных переводов) возникает от трения в узлах вагонов при входе и выходе из кривой и от трения колес о наружный рельс кривой. Величина этого сопротивления зависит от скорости скатывания вагона, длины и радиуса кривой.

Удельное сопротивление движению отцепа на стрелочном переводе возникает от ударов колес на стрелочном переводе (об остряки, крестовины и контррельсы).

Удельная работа сил сопротивления от стрелочных переводов и кривых wск

определяется по формуле (м эн. в.):

углов поворота кривых, включая стрелочные углы на расчетном участке,

град.; 0,56 и 0,23 – эмпирические коэффициенты.

4.4.5. Удельное сопротивление движению отцепа от снега и инея В зимних условиях необходимо учитывать дополнительную работу при преодолении сопротивления движению вагона от снега и инея в пределах

где wсн – удельное сопротивление движению вагона от снега и инея, кгс/тс.

Расчет сопротивления движению от снега и инея ведется только при отрицательных температурах. Значение удельного сопротивления движению вагона от снега и инея устанавливается в зависимости от весовой категории отцепа и температуры наружного воздуха по табл. 4.3, /2/.