РОСЖЕЛДОР

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«Сибирский государственный университет путей сообщения»

Кафедра «Логистика, коммерческая работа и подвижной состав»

Выбор оптимальной транспортно-логистической схемы доставки груза

Курсовая работа

по дисциплине «Транспортная логистика»

Руководитель Разработал

преподаватель студент гр. Д-313

Байдина И.А. Подпорин В.Д.

(подпись) (подпись)

. .

(дата) (дата сдачи на проверку)

Краткая рецензия:

.

(запись о допуске к защите)

. .

(оценка по результатам защиты) (подпись руководителя)

Новосибирск

2017

СОДЕРЖАНИЕ

1. Выбор рациональной схемы транспортировки товара с использованием анализа полной стоимости………………………………………………………..5

1.1 Задача №1……………………………………………………………….5

1.2 Задача №2……………………………………………………………10

2. Выбор оптимальной схемы перевозки груза в прямом смешанном сообщении с использованием сетевого графика………………………………14

3. Разработка графика работы автотранспорта при осуществлении централизованного завоза-вывоза контейнеров……………………………….19

4. Разработка контактного графика работы грузового пункта………………..26

Приложение А……………………………………………………………………32

Список литературы………………………………………………………………33

2 Выбрать оптимальную схему перевозки груза в смешанном сообщении, с использованием сетевого графика

Сетевая модель – важный класс оптимизационных задач, пересекающийся с задачами календарного планирования, которые в общем случае сводятся к построению плана комплекса работ, состоящего из отдельных взаимообусловленных элементарных операций.

Сетевое планирование базируется на структурной таблице:

1) перечень элементарных работ комплекса;

2) перечень работ, на которые опираются элементарные работы;

3) время выполнения каждой работы.

Сетевой график смешанных перевозок можно представить как ряд совокупности, состоящих из элементарных работ, которые должно быть последовательно выполнены. При этом совокупности являются альтернативными друг другу.

Работа на графике показывается в виде векторов, точки начала и окончания которых являются узлами графика.

Критерии выбора варианта:

• время транспортировки Т;

• стоимость С;

• приведенная стоимость С^*.

С^* = (С_гр+С_т)*(1+Δ)ⁿ, (2.1)

где С_гр– закупочная стоимость товара (50 т.руб.);

С_т – стоимость перевозки;

(1+Δ)ⁿ – множитель наращивания % по процентной ставке на годовой период.

Построим схему движения, учитывающую все операции, которые будут выполнены при перевозке (Рисунок 3.1).

Рисунок 3.1 Схемы движения маршрутов

Полученные значения не дают однозначного выбора маршрута, т. к. нет минимального значения в только одном. В сложившейся ситуации будем использовать дополнительные критерии:

1) Лапласа

2) Вальда

3) Сэвиджа

4) Гурвица

Эти критерии позволяют принять решения в условиях неопределенности на основе анализа матрицы возможных вариантов. Строки соответствуют возможным действиям R_j, столбцы – возможным состояниям природы S_i (критерии доставки). Элементы матрицы – результаты при выборе j-го действия и реализации i-го состояния В_ji.

Критерий Лапласа опирается на принцип недостаточного обоснования, согласно которому все состояния природы S_i=(i-n) полагаются равновероятным.

Для принятия решений Лапласа используется формула:

Выбирается минимальное значение.

Критерий Вальда (минимальный или максимальный). Он основывается на принципе наибольшей осторожности. Когда В_ji представляет собой потери, мы используем минимальный критерий.

Критерий Сэвиджа основан на принципе минимизации потерь Для решения задачи составляется матрица потерь, которая называется матрицей рисков r_ji , которая получается путем вычитания из текущего элемента каждого столбца наименьшего элемента каждого столбца. Критерий Сэвиджа считается по формуле:

Критерий Гурвица позволяет управлять степенью «оптимизма - пессимизма». Введем некоторый коэффициент a, который назовем коэффициентом доверия или коэффициентом оптимизма. Этот коэффициент можно интерпретировать как вероятность, с которой произойдет наилучший исход. Исходя из этого, наихудший вариант можно ожидать с вероятностью (1-α). Если вероятности благоприятной и неблагоприятной ситуации равны, то следует принять α=0,5. Для реализации критерия по формуле:

Для наглядности приведу расчеты первого маршрута.

Относительное время транспортировки:

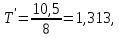
Относительная стоимость:

Относительная приведенная стоимость:

Критерий Лапласа:

Критерий Сэвиджа:

Критерий Гурвица:

Варианты возможных маршрутов представлены в таблице 2.1

Вывод: Наилучший маршрут по критериям Лапласа, Вальда, Сэвиджа, Гурвица является №2(4): 1-2-4-12-14-15 – от Хельсинки до Москвы железной дорогой, по Москве - автотранспортом.

Таблица 2.1 - Варианты возможных маршрутов

№ маршрута	Схема доставки	Время, Т	Стоимость, С	Приведенная стоимость, С*	Относительное значение параметра			Критерии
					Т’	С’	С*’	Лапласа	Вальда	Сэвиджа	Гурвица
1(1)	1-2-3-12-13-15	10,5	2830	2895,1	1,313	3,212	3,086	2,537	3,212	2,212	2,262
1(2)	1-2-3-12-14-15	8	2925	2986,9	1	3,320	3,184	2,501	3,320	2,320	2,160
2(3)	1-2-4-12-13-15	15,5	881	938,2	1,938	1	1	1,313	1,938	0,938	1,469
2(4)	1-2-4-12-14-15	13	976	1032,7	1,625	1,108	1,101	1,278	1,625	0,625	1,363
3(5)	1-2-5-6-7-8-12-13-15	15	2117	2183,3	1,875	2,403	2,327	2,202	2,403	1,403	2,139
3(6)	1-2-5-6-7-8-12-14-15	12,5	2212	2276,2	1,563	2,511	2,426	2,166	2,511	1,511	2,037
3(7)	1-2-5-6-7-9-12-13-15	13	2117	2181,1	1,625	2,403	2,325	2,118	2,403	1,403	2,014
3(8)	1-2-5-6-7-9-12-14-15	10,5	2212	2273,9	1,313	2,511	2,424	2,082	2,511	1,511	1,912
3(9)	1-2-5-6-7-10-12-13-15	14	2201	2266,8	1,750	2,498	2,416	2,221	2,498	1,498	2,124
3(10)	1-2-5-6-7-10-12-14-15	11,5	2296	2359,5	1,438	2,606	2,515	2,186	2,606	1,606	2,022
4(11)	1-2-5-6-7-11-12-13-15	18,5	1760	1826,8	2,313	1,998	1,947	2,086	2,313	1,313	2,130
4(12)	1-2-5-6-7-11-12-14-15	16	1855	1920,3	2	2,106	2,047	2,051	2,106	1,106	2,053
-	-	-	-	-	-	-	-	min=1,278	-	-	-