
- •Классификация горных пород и массивов
- •2. Физико-механические свойства связных горных пород
- •2.1. Упругость
- •2.2. Пластичность и хрупкость
- •2.3. Разрыхление и усадка
- •2.4. Трение
- •3. Некоторые особенности сыпучих и плывучих пород
- •3.1. Общие сведения
- •3.2. Гранулометрический состав (гмс)*
- •3.3. Сжимаемость сыпучей породы
- •3.4. Сопротивляемость сдвигу (срезу)
- •3.5. Плывучие породы (плывуны)
- •3.6. Задачи и примеры к разделу 3*
- •4. Особенности горных пород как * среды
- •4.1. Минимальный размер образцов*
- •4.2. Надежное число испытаний образцов*
- •4.3. Задачи и примеры к разделу 4*
- •5. Напряженное состояние горных пород и устойчивость горных выработок
- •5.1. .Основные понятия*
- •5.2. Напряжение в породном массиве
- •Средних горизонтальных напряжения к вертикальным от глубины:
- •5.3 Модуль упругости при сложном напряженном состоянии
- •5.4.2. Горизонтальная выработка круглой формы
- •Около круглой горизонтальной выработки:
- •5.4.3. Горизонтальные выработки других форм сечения
- •5.5. Задачи и примеры к разделу 5
- •6. Прочность горных пород и массивов*
- •6.1 Общие сведения
- •6.2. Теории прочности горных пород
- •6.2.1. Классические теории прочности
- •6.2.2. Теория прочности о. Мора*
- •Паспорта прочности породы
- •6.3. Лабораторные методы определения прочности * породных образцов
- •6.3.1. Прочность при одноосном сжатии
- •На одноосное сжатие
- •6.3.2. Прочность при одноосном растяжении
- •6.3.3. Прочность при сдвиге (срезе)
- •6.3.4. Стабилометрические испытания образцов горных пород
- •По данным стабилометрических испытаний образцов пород
- •6.3.5. Коэффициент крепости горной породы по шкале проф. Протодьяконова м.М.
- •6.3.6. Паспорт прочности и коэффициент крепости породы м.М. Протодьяконова
- •6.4. Задачи и примеры к разделу 6
- •7. Проявление горных процессов при открытых горных работах
- •7.1. Устойчивость откоса при наличии вероятной поверхности скольжения
- •7.2. Устойчивость откоса при однородных слабых породах
- •7.3.Устойчивость откоса в неоднородных породах
- •7.4. Задачи и примеры к разделу 7
- •8. Проявление горного давления в подземных протяженных выработках Общие сведения
- •Влияние структурных элементов на устойчивость обнажений пород
- •8.3. Влияние напряженно-деформированного состояния пород на устойчивость их обнажений в горных выработках
- •8.4. Простейшие теории и методы расчета горного давления
- •8.4.1. Горизонтальные выработки
- •8.4.2. Наклонные выработки
- •8.4.3. Вертикальные выработки
- •8.5. Горное давление и крепь выработки
- •8.5.1. Давление на контуре выработки, пройденной в напряженном горном массиве
- •8.5.2. Рабочая характеристика горных крепей
- •Взаимодействие крепи с породным массивом
- •8.5.4. Формулы для расчета горного давления с учетом смещения крепи
- •Круглого сечения:
- •Некруглой формы
- •8.6. Задачи и примеры к разделу 8
- •Показатель устойчивости обнажения:
- •9. Проявление горного давления в подземных очистных выработках
- •9.1. Выбор безопасных размеров камер
- •9.1.1. Метод Южно-Африканского Совета по промышленным и научным исследованиям
- •9.1.2. Метод Норвежского института геомеханики
- •9.2. Расчет прочных размеров целиков
- •9.2.1. Общие сведения
- •9.2.2. Метод л.Д. Шевякова.
- •9.2.3. МетодГ.Е. Гулевича
- •9.2.4. Энергетический критерий устойчивости целиков
- •9.2.5. Метод оценки устойчивости целиков д.Ф. Коутса
- •9.3. Горное давление в закрепленных забоях
- •9.4. Методы управления горным давлением
- •9.5. Задачи и примеры к разделу 9
- •Приложения
- •Приложение 6
- •Приложение 7
- •Приложение 17
- •Литература
- •Содержание
5. Напряженное состояние горных пород и устойчивость горных выработок
5.1. .Основные понятия*
Пусть твердое тело U (рис. 12.а) находится в равновесии под действием внешних сил Р, Р1, Р2, Р3, Р4.В сечении внешние силы уравновешиваются внутренними силами (напряжениями).
Рассмотрим
небольшую площадку в сечении S
(рис. 12.б)
величиной S
около точки А.
Пусть на нее действует сила
![]() .
Тогда среднее напряжение на площадке
.
Тогда среднее напряжение на площадке
![]() составит:
составит:
![]() .
.

Рис. 12. Схема напряженного состояния твердого тела:
а – силы Р, Р1, Р2, Р3, Р4 находятся в равновесии;
б
– напряжение на площадке
![]()
Истинное напряжение в точке А составит:
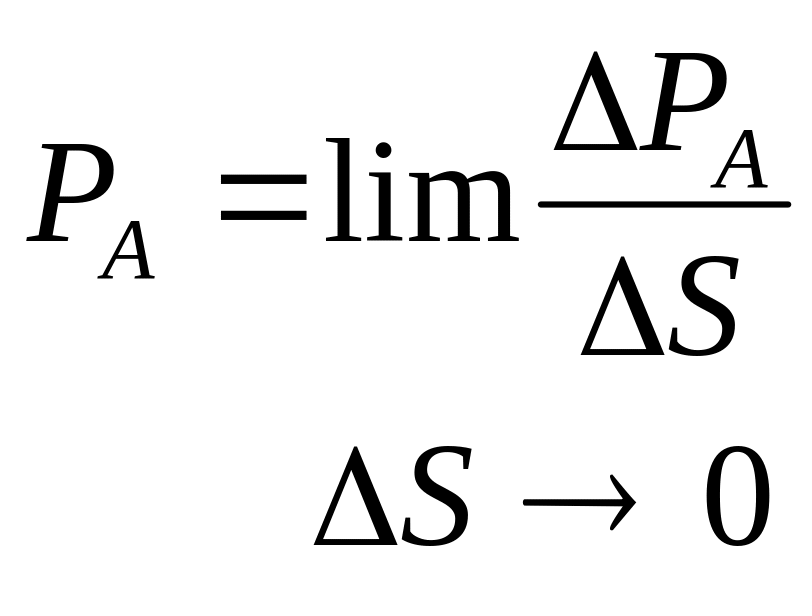 .
.
Напряжение в точке А можно разложить на две составляющие:
![]() ,
,
где
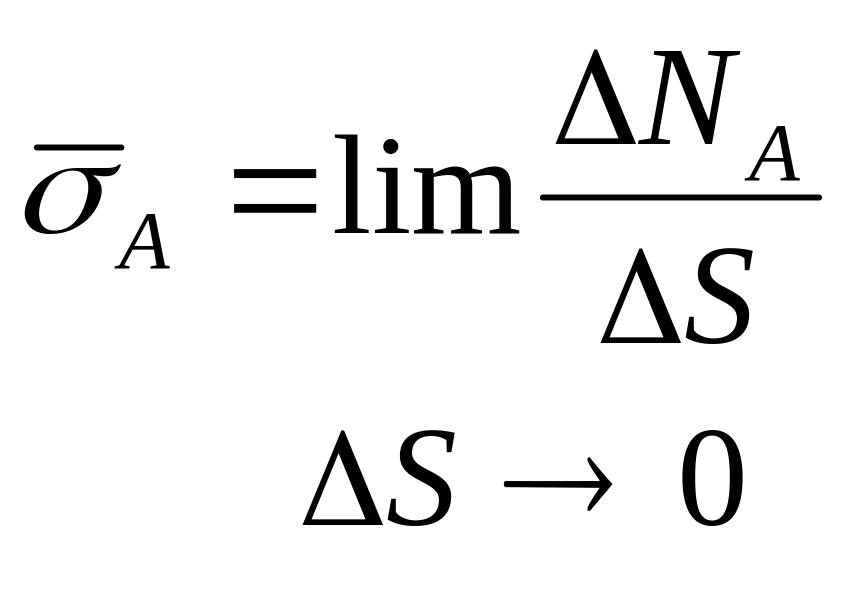 – нормальное
напряжение;
– нормальное
напряжение;
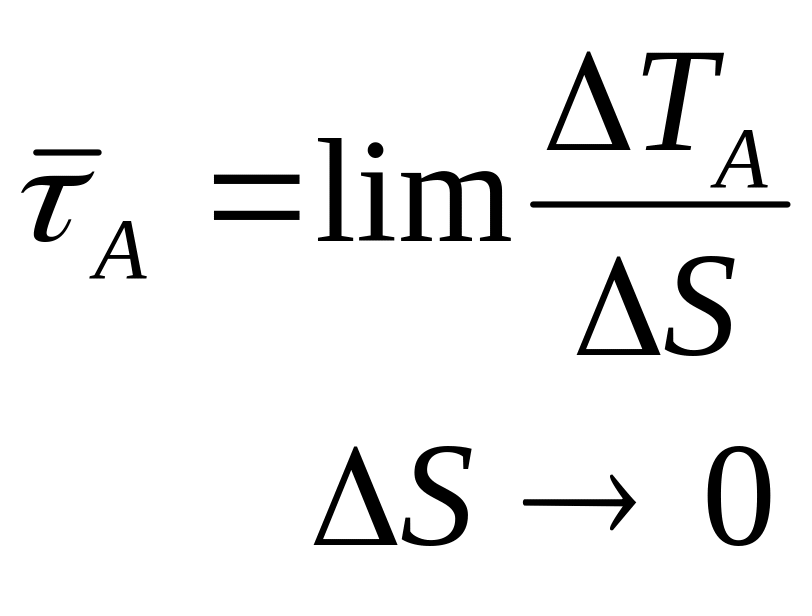 – касательное
напряжение.
– касательное
напряжение.
В теории упругости доказывается, что для любой точки тела, при любом напряженном состоянии имеются три взаимно перпендикулярные плоскости, на которых касательные напряжения отсутствуют. Нормальные напряжения на этих площадках называются главными нормальными напряжениями и обозначаются σ1, σ2, σ3, причем σ1> σ2> σ3, Нормали к указанным площадкам называются главными осями напряжений и обозначаются соответственно 1, 2, 3. Касательные напряжения на площадках, делящих пополам угол между главными осями, называются главными касательными напряжениями и обозначаются (рис. 13)
τ12 = τ21; τ23 = τ32; τ31 = τ13.

Рис.13. Площадки главных касательных напряжений
Величины главных касательных напряжений составляют
![]() .
.
На площадках главных касательных напряжений нормальные напряжения составляют
![]() .
.
5.2. Напряжение в породном массиве
Рассмотрим напряженное состояние кубика породного массива, расположенного на глубине H = Z от поверхности (рис.14). Обозначим вертикальное напряжение σz и горизонтальные – σx и σy. Тогда относительные деформации кубика можно выразить в виде
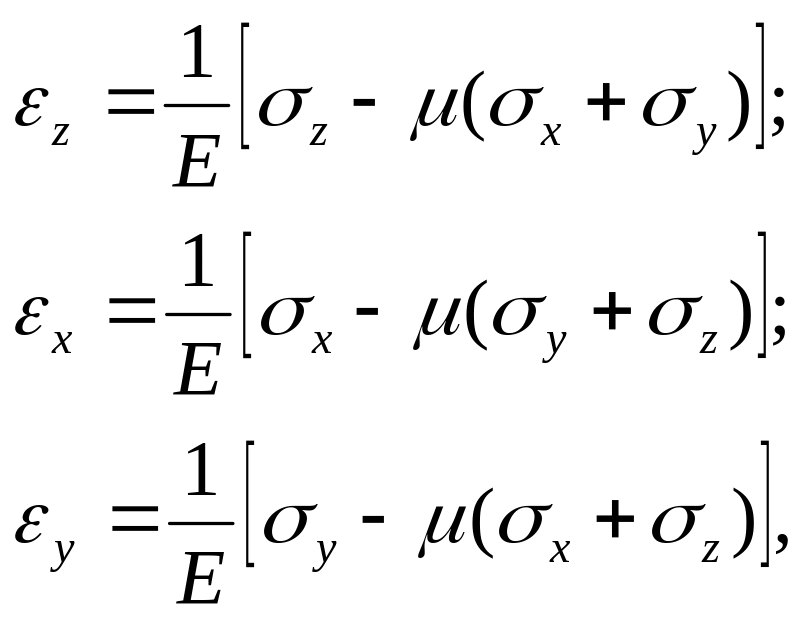
где:
Е – модуль упругости массива в простом напряженном состоянии.

Рис. 14. Схема напряженного состояния породного массива
В 1952 г. Терцаги и Рихарт внесли предложение принять εх = εу = 0, откуда следует:
![]() .
.
Эта зависимость, по-видимому, имеет место в крепких горных породах при относительно небольших напряжениях.
В
1912 г. Гейм предложил считать
![]() на том основании, что с течением времени
напряженное состояние пород выравнивается.
Предложение Гейма, по-видимому, можно
принять для пластичных пород, особенно
на глубинах более 1 км.
на том основании, что с течением времени
напряженное состояние пород выравнивается.
Предложение Гейма, по-видимому, можно
принять для пластичных пород, особенно
на глубинах более 1 км.
На рис.15 приведена зависимость вертикального напряжения в горном массиве σz от глубины Z на основе натурных наблюдений.
Эта зависимость выражается формулой:
![]() ,
,
где
γ – средневзвешенный объемный вес пород;
z – глубина от поверхности.
На рис. 16 приведена зависимость от глубины отношения средних горизонтальных напряжений к вертикальным. Это отношение укладывается в область, ограниченную кривыми :
![]() .
.
Из графика рис.16 видно, что на малых глубинах (до 500 м) горизонтальные напряжения значительно выше вертикальных. На глубинах 1 км и более значения горизонтальных и вертикальных напряжений выравниваются. Все это говорит о важности натурных замеров напряженного состояния горных пород при решении горных задач.

Рис. 15. Зависимость вертикального напряжения от глубины:
● Австралия, ▼ Канада, ▲ США, ○ Скандинавские страны,
■ Южная Африка, □ другие районы

Рис. 16. Зависимость отношения
