В.Ф. Гусев

ПРАКТИКУМ

Учебное пособие

Москва – 2010

Гусев В.Ф.

Практикум

В пособии рассматриваются основные физико-механические и прочностные свойства горных пород и массивов и методы их определения, методы оценки прочности породного массива по данным испытаний образцов, напряженное состояние в горном массиве при проведении горных выработок, проявление горного давления при подземных и открытых горных работах. Пособие содержит задачи по наиболее существенным разделам дисциплины. Каждая задача представлена в решенном варианте, после чего предлагается подобная задача с несколькими вариантами для самостоятельной работы. Решение задач облегчается наличием кратких теоретических предпосылок.

Учебное пособие предназначено для студентов МГОУ, обучающихся по направлению 550600 «Горное дело», а также может быть полезным для студентов других горных вузов и факультетов.

Автор выражает глубокую благодарность профессору Панину Ивану Михайловичу за помощь при подготовке данной рукописи.

1. Классификация горных пород и массивов

Из многочисленных классификаций приводим лишь некоторые, имеющие наиболее близкое отношение к рассматриваемому курсу.

По характеру связи минеральными частицами горные породы делятся на связные и раздельнозернистые. Связные породы, в свою очередь, делятся на твердые с жесткими связями (кристаллические) и мягкие с пластичными связями (глины).

Раздельнозернистые породы делятся на сыпучие (например песок в сухом состоянии) и плывучие (насыщенные водой мелкозернистые породы – плывуны).

По трещиноватости породные массивы делятся на:

• нетрещиноватые (сплошные);

• слаботрещиноватые: с одной системой трещин при расстоянии между трещинами более 1 м;

• среднетрещиноватые: с двумя системами взаимно пересекающихся трещин при среднем расстоянии между трещинами более 1 м;

• сильнотрещиноватые: с несколькими системами взаимно пересекающихся трещин при среднем расстоянии между трещинами 0,5 м;

• весьма сильнотрещиноватые: с несколькими системами взаимно пересекающихся трещин при среднем расстоянии между трещинами менее 0,2 м.

По слоистости породные массивы делятся на:

• весьма тонкослоистые при мощности слоев менее 0,2 м;

• тонко слоистые при мощности слоев 0,2–1,0 м;

• крупнослоистые при мощности слоев 3–10 м;

• весьма крупно слоистые при мощности слоев более 10 м.

По устойчивости обнажений породные массивы делятся на:

• неустойчивые: обрушаются вслед за подвиганием забоя;

• слабоустойчивые: в призабойной полосе шириной до 1 м устойчивые в течение 2–3 ч;

• среднеустойчивые: в призабойной полосе шириной до 2 м устойчивые до 1 сут.;

• весьма устойчивые: в призабойной полосе шириной до 5–6 м обладают длительной устойчивостью.

2. Физико-механические свойства связных горных пород

В данном разделе не рассматриваются прочностные свойства, которые представлены в разделе «Прочность горных пород и массивов».

2.1. Упругость

Под упругостью тела понимают его способность изменять форму и размеры под действием силы и восстанавливать их после снятия силы.

Упругое тело подчиняется закону Гука: деформация пропорцианальна действующей силе. При простом (одноосном) растяжении или сжатии (рис. 1) выражение закона Гука имеет вид:

,

где

Р – действующая сила;

l – длина базы измерения на образце до приложения силы;

Е – коэффициент пропорциональности (модуль упругости образца 1 рода);

S – площадь поперечного сечения образца до приложения нагрузки.

В соответствие с рис. 1:

– абсолютная продольная деформация образца;

– абсолютная поперечная деформация образца.

Отношение называется относительной продольной деформацией образца.

Отношение называется относительной поперечной деформацией образца.

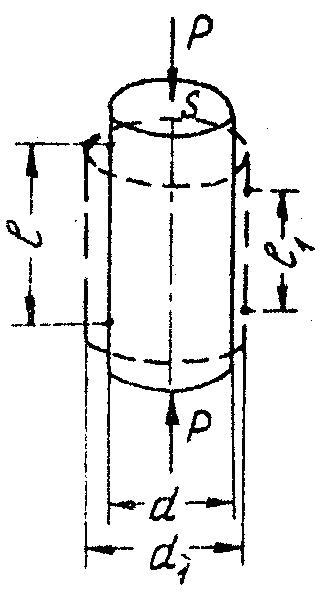
Рис. 1. Упругое сжатие

Отношение называется коэффициентом поперечной деформации образца (коэффициент Пуассона).

Приведенную выше формулу можно представить в виде:

или .

Откуда ,

где – нормальное напряжение.

Графическая зависимость между σ и ε носит название «напряжение – деформация» (рис. 2–5).

По виду диаграммы «напряжение – деформация» тела разделяются на абсолютно упругие, вполне упругие, упругие и неупругие.

Для абсолютно упругого тела (рис. 2):

.

Для вполне упругого тела (рис. 3):

; .

Для упругого тела (рис. 4) модули упругости при нагружении Е_н и разгрузки Е_р различны. Работа нагружения А_н больше работы разгрузки А_р на величину рассеянной энергии L:

.

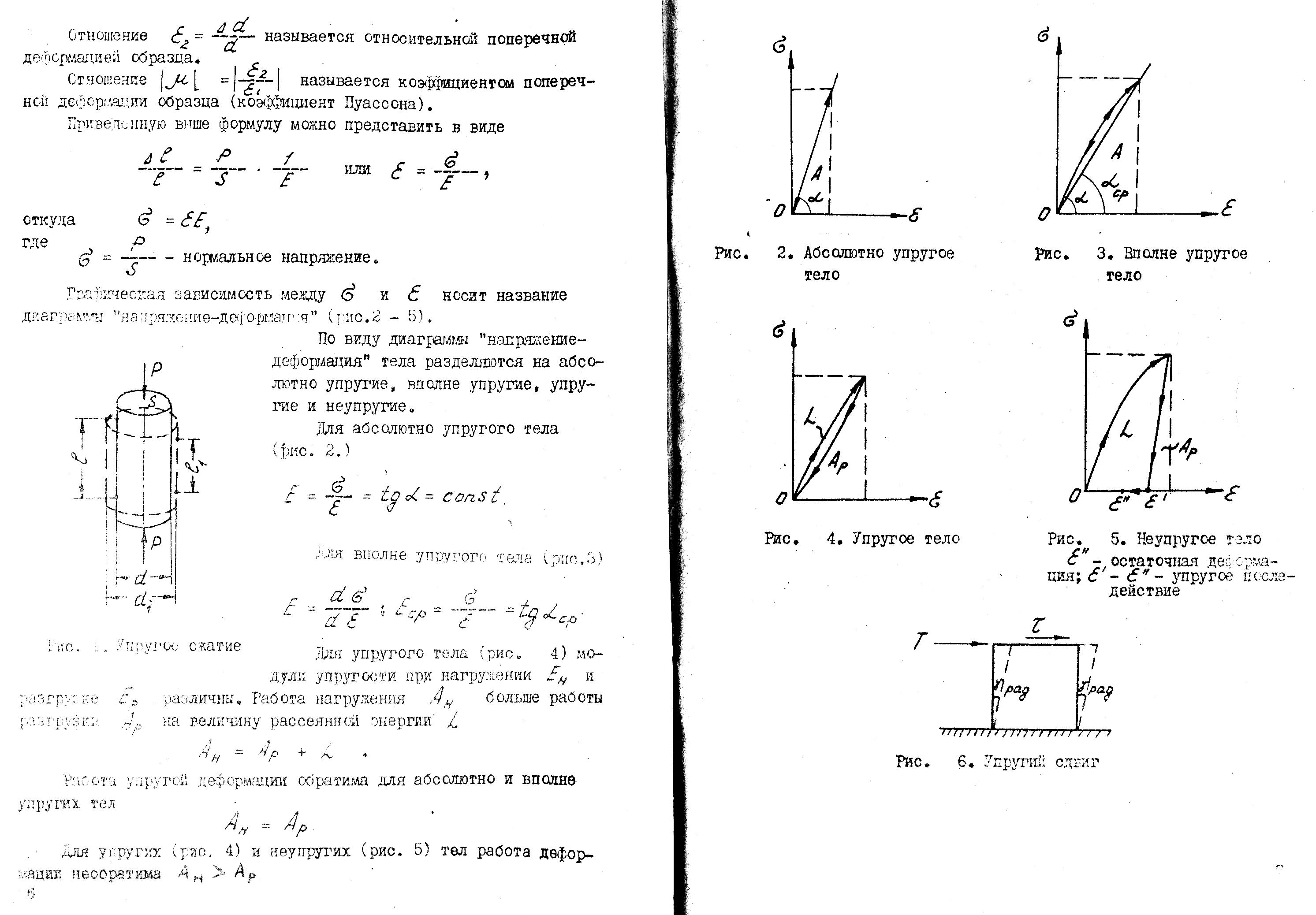
Рис. 2. Абсолютное упругое тело

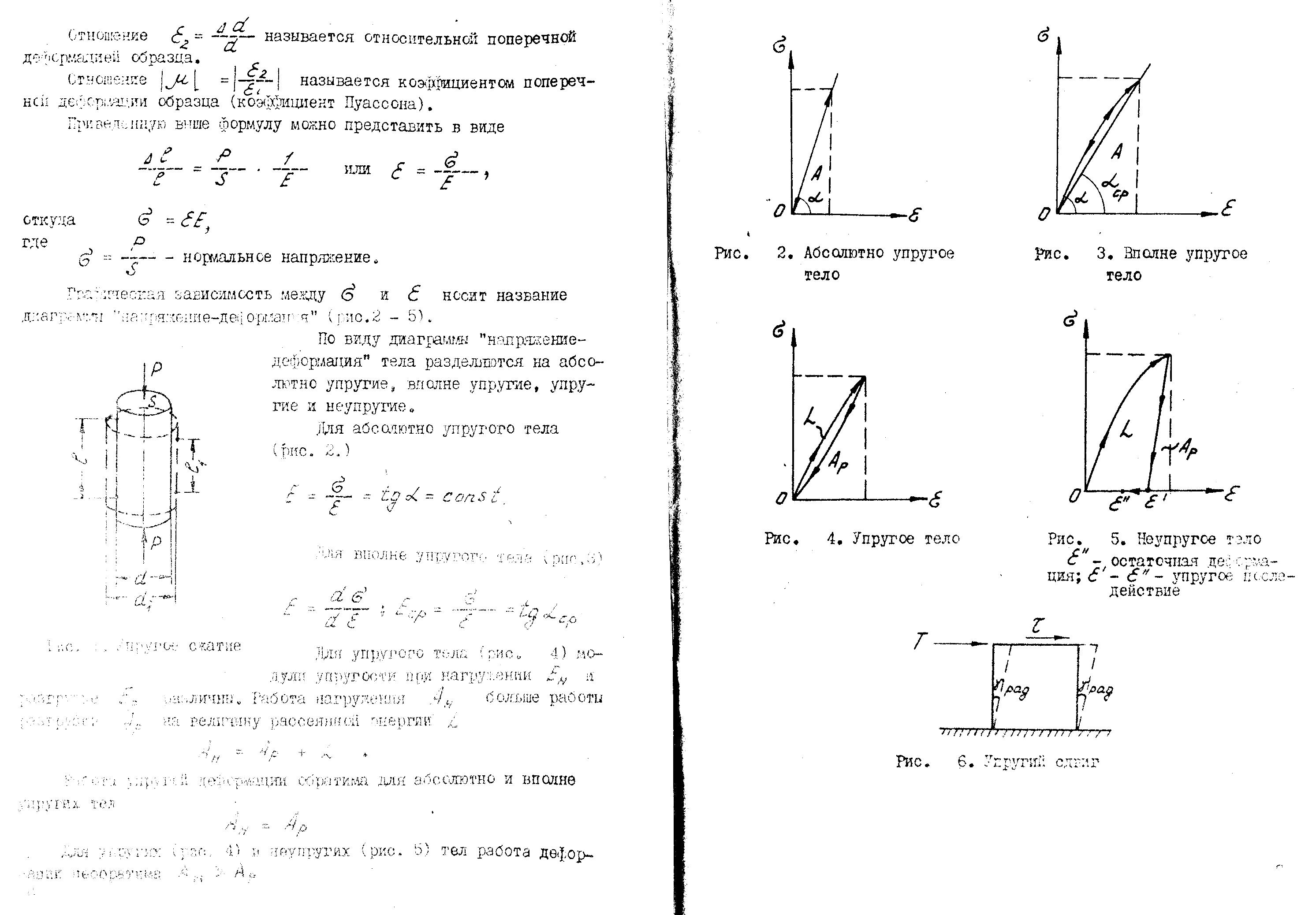
Рис. 3. Вполне упругое тело

Рис. 4. Упругое тело Рис. 5. Неупругое ело

– остаточная деформация;

– упругое последействие

Работа упругой деформации обратима для абсолютно и вполне упругих тел

Для упругих (рис. 4) и неупругих (рис. 5) тел работа деформации необратима

Физико-механические свойства горных пород меняются с изменением величины напряжения. При малых напряжениях большинство из них проявляет упругие свойства.