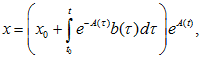Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят явно производные искомых функций до некоторого порядка. Если неизвестными являются функции двух или более переменных, то уравнения называются уравнениями в частных производных. В противном случае, то есть если искомая функция зависит только от одного вещественного независимого переменного, уравнения называются обыкновенными дифференциальными уравнениями. В этом курсе будем иметь дело только с последними.

Так как во многих физических приложениях независимым переменным, от которого зависят неизвестные искомые функции, является время, то в дальнейшем, как правило, независимое переменное будет обозначаться через t. Неизвестные функции будут обозначаться через x, y, z и т.д.

Рассмотрим в первую очередь одно дифференциальное уравнение первого порядка. Общий вид такого уравнения следующий:

Здесь t - независимое переменное, x - неизвестная функция, зависящая от t.   - ee производная. F - заданная функция трех вещественных переменных. Функция F, вообще говоря, может быть задана не для всех значений своих аргументов, поэтому следует говорить об области  задания функции F, имея в виду область координатного пространства трех (вещественных) переменных t, x,  .

Уравнение (1.1) называется уравнением первого порядка потому, что в него входит лишь производная первого порядка от неизвестной функции x.

Решением уравнения (1.1) называется такая функция x =(t) независимого переменного t, определения на некотором интервале r₁  <  t  <  r₂ (случаи r₁ =  и r₂ = +  не исключаются), которая дифференцируема в каждой точке этого интервала и при подстановке ее вместо x в соотношение (1.1) мы получаем тождество (по t) на всем интервале r₁ < t < r₂.

Интервал r₁ < t < r₂ называется интервалом определения решения (t).

Очевидно, что подстановка функции x =(t) в соотношение (1.1) возможна только в том случае, когда точка с координатами (t,(t),  ) принадлежит области  определения функции F при произвольном t из интервала r₁ < t < r₂.

Соотношение (1.1) связывает три переменные: t, x,  . В некоторых случаях из (1.1) переменная   может быть выражена в виде однозначной функции переменных t, x. В этом случае дифференциальное уравнение (1.1) равносильно дифференциальному уравнению вида

Дифференциальное уравнение (1.2) называется разрешенным относительно производной или уравнением нормального вида; Именно уравнения нормального вида мы и будем теперь рассматривать. Мы не будем уже считать, что соотношение (1.2) получено в результате разрешения относительно   уравнения вида (1.1), а будем исходить из функцииf(t,x) как из заданной функции двух независимых переменных t, x.

Для того, чтобы пользоваться геометрическими представлениями и терминологией, введем в рассмотрение координатную плоскость R² переменных t и x. Функция f, определяющая дифференциальное уравнение (1.2), может быть задана не для всех значений своих аргументов t и x, т.е. не на всей плоскости R²(t,x), а лишь в точках некоторого множества D этой плоскости. Относительно множества D в дальнейшем всегда будем предполагать, что оно является открытым, а функция fявляется непрерывной относительно пары переменных t, x на всем множестве D.

График _={(t,(t)),  r₁ < t < r₂} решения x =(t) уравнения (1.2) называется интегральной кривой этого дифференциального уравнения.

Интегральная кривая представляет собой кривую в плоскости R² с уравнением x =(t), имеющую в каждой точке касательную и полностью проходящую в открытом множестве D.

Итак, интегральная кривая - геометрическая интерпретация решения дифференциального уравнения. Возможна геометрическая интерпретация и самого уравнения (1.2). Именно, через каждую точку (t,x) множества D проведем прямуюl_t,x с угловым коэффициентом f(t,x). Мы получаем поле направлений, соответствующее уравнению (1.2), что и является геометрической интерпретацией этого уравнения.

Связь между геометрической интерпретацией уравнения и геометрической интерпретацией его решения заключается в том, что любая интегральная кривая x =(t) в каждой своей точке (t,(t)) касается прямой l_t,(t).

Теорема существования и единственности.

В теории дифференциальных уравнений важным теоретическим вопросом является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и поэтому приходится ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решений данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности, которая в этом параграфе приводится без доказательства. Сначала приведем подготовительный материал.

Пусть t₀, x₀ - произвольная точка множества D, в котором определена правая часть f(t,x) уравнения (1.2).

Задача отыскания решения x =(t) этого уравнения, удовлетворяющего дополнительному условию

называется задачей Коши (или задачей с начальным условием) для уравнения (1.2), а соотношение (1.3) - начальным условием для этого уравнения. Говорят также, что решение x = (t) удовлетворяет начальному условию (1.3) или что оно имеет начальные значения t₀, x₀. Утверждение, что решение x =(t) удовлетворяет начальному условию (1.3) предполагает, что интервал r₁ < t < r₂ определения решения x =(t) содержит точку t₀.

Геометрическая интерпретация задачи Коши состоит в том, чтобы через заданную точку (t₀, x₀) множества D провести интегральную кривую дифференциального уравнения (1.2).

Далее, пусть функция f(t,x) определена на множестве DR²(t,x). Говорят, что эта функция удовлетворяет условию Липшица относительно x (равномерно по t), если существует постоянная M > 0 (не зависящая от t) такая, что:

Постоянная M называется постоянной Липшица.

Теорема 1.1.1 (О существовании и единственности решения задачи Коши) Пусть

- дифференциальное уравнение. Будем предполагать, что функция f(t,x) задана на некотором открытом множестве D плоскости R²(t,x) переменных t, x. Относительно функции f(t,x) будем предполагать, что она непрерывна на D и удовлетворяет на этом множестве условию Липшица (1.4) относительно x (равномерно по t). Теорема утверждает, что:

1) для всякой точки (t₀, x₀)  D найдется решение x = (t) уравнения (1.5), удовлетворяющее начальному условию

2) если два решения x = (t) и x = (t) уравнения (1.5) совпадают хотя бы для одного значения t₁, т.е. если

то эти решения тождественно равны для всех значений переменного t, для которых они оба определены.

Таким образом, теорема 1.1.1 утверждает, что координаты любой точки (t₀, x₀) множества D являются начальными значениями для некоторого решения уравнения (1.5) и что два решения с общими начальными значениями совпадают на пересечении их интервалов определения.

Геометрическое содержание теоремы 1.1.1 заключается в том, что через каждую точку (t₀, x₀)  D проходит одна и только одна интегральная кривая уравнения (1.5).

Говоря, что через каждую точку (t₀, x₀)  D проходит "только одна" интегральная кривая, мы допустили некоторую неточность. Действительно, решением уравнения (1.5) называется функция x = (t), заданная на вполне определенном интервале r₁ < t < r₂. Наряду с этой функцией может существовать функция x = (t), также удовлетворяющая уравнению (1.5) и начальному условию (1.6), заданная на другом интервале s₁ < t < s₂. Вторая часть теоремы 1.1.1 утверждает лишь, что функции (t) и (t) совпадают лишь там, где они обе определены, но вовсе не утверждает, что их интервалы определения r₁ < t < r₂ и s₁ < t < s₂ одинаковы.

Говорят, что решение x = (t), заданное на интервале s₁ < t < s₂ является продолжением решения x =(t), заданного на интервале r₁ < t < r₂, если   (r₁,r₂)  (s₁,s₂)   и   (t)  (t)     t  (r₁,r₂). Решение называется непродолжаемым, если не существует никого отличного от него продолжения. Далее будет доказано, что каждое решение может быть продолжено до непродолжаемого, причем единственным образом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение теоремы 1.1.1 о том, что через каждую точку (t₀, x₀)  D проходит единственная интегральная кривая, становиться точным.

Замечание к теореме 1.1.1. Если правая часть f(t,x) уравнения (1.5) не удовлетворяет условию Липшица (1.4), то вторая часть теоремы (о единственности), вообще говоря, не справедлива. Действительно, рассмотрим уравнение

Правая часть этого уравнения определена и непрерывна при всех x, однако условию Липшица в областях, содержащих точки (t,0), не удовлетворяет, ибо для точек (t,0), (t,x) не существует постоянной M > 0 такой, что

С другой стороны, ясно, что в любой области P плоскости R²(t,x), не пересекающейся с прямой x = 0, к уравнению (1.7)теорема 1.1.1 применима, и таким образом, в каждой из полуплоскостей x > 0 и x < 0 через каждую точку проходит единственная интегральная кривая, уравнение которой можно найти явно. Действительно, нетрудно убедиться, что при любой постоянной c функция

уравнению (1.7) удовлетворяет.

Часть графика функции (1.8) (при t < c) проходит в полуплоскости x < 0, часть же (при t > c) - в полуплоскости x > 0. Функция x  0, очевидно, также является решением уравнения (1.7).

Таким образом, через каждую точку (t,x) = (c,0) проходят два решения уравнения (1.7): решение (1.8) и решение x  0.

В качестве иллюстрации теоремы 1.1.1 рассмотрим задачу об отыскании всех решений простейшего дифференциального уравнения

где  - действительная постоянная. В данном случае правая часть f(t,x) = x определена на всей плоскости (t,x) и удовлетворяет на ней условию Липшица с постоянной M = . Таким образом, теорема 1.1 к уравнению (1.9) применима. Непосредственной подстановкой убеждаемся, что каждая функция

где C - произвольное действительное число, является решением уравнения (1.9). Интервалом определения решения (1.10)является вся прямая t  (,+) и поэтому оно является непродолжаемым. Покажем, что формула (1.10) исчерпывает все решения уравнения (1.9). Действительно, пусть x =(t) - произвольное решение этого уравнения, заданное на интервале r₁< t < r₂. Пусть t₀  (r₁,r₂) - произвольная точка и x₀ = (t₀). Если в качестве постоянной C принять величину

то тогда два решения x = (t) и   уравнения (1.9) имеют одинаковые начальные значения t₀, x₀ и поэтому в силу второй части теоремы 1.1.1 совпадают. Таким образом, придавая постоянной C в (1.10) всевозможные значения, мы получим все решения уравнения (1.9).

В этом параграфе мы приведем методы интегрирования в квадратурах некоторых простейших уравнений первого порядка.

I. Уравнения в полных дифференциалах

Рассмотрим уравнение вида

правая часть которого представлена в виде отношения двух функций g(t,x) и h(t,x). Предполагается, что функции g(t,x) иh(t,x) определены и непрерывны на некотором открытом множестве D плоскости переменных (t,x) и знаменатель h(t,x) не обращается в нуль ни в одной точке этого множества. Уравнение (1.11) часто символически записывают в виде

Уравнение (1.11) называется уравнением в полных дифференциалах, если левая часть равенства (1.12) представляет собой полный дифференциал некоторой функции F(t,x) на всем множестве D, т.е.

Таким образом,

Справедливо следующее утверждение:

Для каждого решения x =(t) уравнения (1.11) имеет место тождество

Обратно, каждая функция x =(t), заданная на некотором интервале и определяемая как неявная функция из уравнения

(C - произвольная постоянная), является решением дифференциального уравнения (1.11).

Действительно, пусть x =(t) - решение уравнения (1.11) с интервалом определения r₁ < t < r₂. Тогда мы имеем, что

Отсюда получаем

В силу (1.14) тогда имеем

т.е.

Таким образом, F(t,(t)) есть константа на всем интервале (r₁,r₂).

Обратно, предположим что x =(t) есть решение уравнения (1.15), определенное на некотором интервале, так что

Дифференцируя это тождество по t, мы в силу (1.14) получаем:

Отсюда видно, что x = (t) есть решение дифференциального уравнения (1.11). Утверждение доказано.

Из сказанного выше ясно, что решение конкретного уравнения в полных дифференциалах состоит в практическом нахождении функции F(t,x). Если функции h(t,x) и g(t,x) обладают непрерывными частными производными по t и x, то из (1.14) следует соотношение

Тождество (1.16), как известно, является необходимым, а в случае односвязной области D и достаточным условием того, что выражение

есть полный дифференциал некоторой функции F(t,x). Из курса математического анализа известно, что функцию F(t,x) можно определить по ее полному дифференциалу hdxgdt, взяв криволинейный интеграл от h(t,x)dx  g(t,x)dt по любому пути L, соединяющему некоторую фиксированную точку (t₀, x₀) и точку (t,x) с текущими координатами:

Часто бывает возможным выбрать в качестве пути L ломаную, состоящую из двух звеньев, параллельных осям координат; в этом случае

В некоторых случаях, когда левая часть уравнения (1.12) не является полным дифференциалом, легко удается подобрать такую функцию (t,x), после умножения на которую левая часть уравнения (1.12) превращается в полный дифференциал

Такая функция  называется интегрирующим множителем. (Заметим, что умножение на интегрирующий множитель может привести к появлению лишних частных решений, обращающих функцию  в нуль). Из соотношения (1.17) следует, что

Если функции , h и g непрерывно дифференцируемы в D, то из (1.18) следует равенство

Если область D односвязна, то равенство (1.19) является (подобно (1.16)) не только необходимым, но и достаточным условием существования функции F(t,x), для которой выполняется тождество (1.17).

В общем случае интегрирование (т.е. нахождение функции ) уравнения (1.19) в частных производных является задачей не более простой, чем решение исходного уравнения (1.11), однако в некоторых случаях подбор частного решения уравнения (1.19) не представляет затруднений.

II. Линейные уравнения

Линейным уравнением первого порядка называют уравнения

где a(t), b(t) - заданные функции переменной t. Предположим, что функции a(t) и b(t) определены и непрерывны на некотором интервале r₁ < t < r₂ (возможно, что r₁ = , r₂ = + одновременно или выполнено одно из этих соотношений). Таким образом, открытое множество D, на котором задана правая часть уравнения (1.20) представляет собой полосу r₁ < t < r₂ на плоскости (t,x), если r₁ и r₂ конечны; полуплоскость, если конечна только одна из величин r₁, r₂ и плоскость, если бесконечны обе величины r₁, r₂. Правая часть уравнения (1.20) непрерывна вместе со своей частной производной по x на всем множестве D и поэтому удовлетворяет (по x) условию Липшица. Итак, для уравнения (1.20) условия теоремы  выполнены.

Пусть t₀ - некоторая точка интервала (r₁,r₂). Положим

Функция A(t), очевидно, определена на интервале r₁ < t < r₂. Докажем, что совокупность всех решений уравнения (1.20)задается формулой

где x₀ - произвольная константа. Для вывода формулы (1.22) рассмотрим сначала однородное уравнение, соответствующее (1.20), т.е. уравнение

Это уравнение в полных дифференциалах. В самом деле, символически его можно записать в виде

Соответствующая функция F(t,x) легко вычисляется:

где A(t) определена по формуле (1.21). В таком случае, согласно вышесказанному, решения уравнения (1.23) определяются как неявные функции из соотношения

Отсюда находим   или

где C может принимать любые действительные значения.

Для получения с помощью формулы (1.24) решения неоднородного уравнения (1.20) применяется так называемый метод вариации постоянной.То есть решение уравнения (1.20) ищется в виде (1.24), но C уже не константа, а некоторая неизвестная функция переменного t. Подставляя выражение

в уравнение (1.20), получим:

или, что то же

Отсюда находим

где x₀ - константа интегрирования. На основании (1.25), (1.26) получаем формулу (1.22).

Некоторые дифференциальные уравнения путем замены переменных могут быть сведены к линейным. К таким уравнениям относится так называемое уравнение Бернулли, имеющее вид

Это уравнение заменой переменной   сводится к линейному. Действительно, так как

то произведя подстановку, получим линейное уравнение

Рассмотрим уравнение Риккати:

Это уравнение в общем виде квадратурой не интегрируется, но может быть заменой переменных сведено к уравнению Бернулли, если известно одно частное решение этого уравнения. Действительно, если x₁ = x₁(t) - известное частное решение, то полагая

получим

Так как

то приходим к уравнению Бернулли

III. Уравнения с разделяющимися переменными

Так называются уравнения

Предположим, что функция f(t) определена и непрерывна на интервале r₁ < t < r₂, а функция g(x) определена, непрерывна и не обращается в нуль на интервале q₁ < x < q₂. Рассматриваемое уравнение есть уравнение в полных дифференциалах. Именно, оно может быть символически записано в виде

а соответствующая функция F(t,x) задается формулой

Здесь x₀  (q₁,q₂),  t₀  (r₁,r₂) - фиксированные точки, а x и t изменяются на этих же интервалах. В силу сказанного в разделе I все решения уравнения (1.27) получаются как неявные функции из соотношения

IV. Однородные уравнения

Уравнение первого порядка

называется однородным, если f(t,x) есть однородная функция своих аргументов нулевой степени однородности, т.е. имеет место тождество

Полагая в (1.28)  , получаем тождество

Таким образом, правая часть по существу зависит только от отношения переменных. Обозначая

видим, что однородное уравнение всегда можно представить в виде

Будем предполагать, что функция h(y) определена и непрерывна на интервале a₁ < y < a₂ и что на этом интервале функцияh(y)  y в нуль не обращается.

Уравнение (1.29) решается посредством замены переменных. Точнее, вместо неизвестной функции x(t) введем новую неизвестную функцию y(t):

Произведя такую подстановку, для новой неизвестной функции y получаем уравнение

Мы получили уравнение с разделяющимися переменными, которое решается способом, указанным в III.

Замечание. Если h(y)  y, то уравнение (1.29) имеет вид

и интегрируется методом разделения переменных (его общее решение - x = Ct). Если h(y)  y обращается в нуль при y = y₀, то кроме решений, получающихся из (1.30), имеется решение  .