Махов а.М.

Сетевые методы планирования

Санкт-Петербург

2013

Введение

Возможность широкого применения сетевых методов анализа и оптимизации в экономических и управленческих задачах обусловлена двумя причинами. Во-первых, современное общество отчасти можно рассматривать как систему сетей, предназначенных для транспортирования, передачи, распределения электроэнергии, товаров и информации. Поскольку каждая из подсистем имеет весьма сложную структуру и является дорогостоящей, возникает необходимость в эффективном использовании уже существующих технических средств и в рациональном проектировании новых. При проектировании и усовершенствовании больших и сложных систем, а также при поиске путей их наиболее рационального использования существенное значение могут иметь методы сетевого анализа.

Во-вторых, для многих задач, не являющихся сетевыми по постановке, при сведении их к задаче на графе, процедура решения может быть существенно упрощена и сделана более наглядной, что является немаловажным в аргументации при реализации полученных результатов на практике.

Данное методическое пособие для обеспечения для самостоятельной работы студентов посвящено двум наиболее часто встречающимся сетевым задачам: построению плана замены оборудования и задаче коммивояжера. Следующие параграфы посвящены краткому изложению необходимого для выполнения работ математического аппарата.

I. Введение в теорию графов Перечень используемых в дальнейшем обозначений

x B - элемент x принадлежит множеству B;

B  A - множество B является подмножеством множества A;

B  A - множество B включает множество A (A  B);

A\B - разность множеств (множество, содержащее все элементы A, не входящие в B);

A В  A  B - множество, являющееся объединением (суммой) множеств A и B;

A B  A  B - множество, являющееся пересечением (произведением) множеств A и B;

{...} - обозначение множества;

 - пустое множество;

A  {B, С} - множество A состоит из подмножеств B и C;

A  {a_i, i N} - множество A состоит из элементов a_i, каждый из которых полностью характеризуется некоторым конкретным значением признака i, все значения которого составляют множество N;

A  B - между всеми элементами множеств A и B установлено взаимно однозначное соответствие;

x_i- сумма значений величины x, характеризуемой признаком i, по всем возможным в промежутке [a, b] значениям этого признака;

x_i- сумма значений величины x, характеризуемой признаком i, по всем возможным значениям этого признака;

a  F (b) - величина a является функцией (зависит от) величины b;

- любой;

: - такой, что;

- бесконечность;

- существует.

1. Определения

С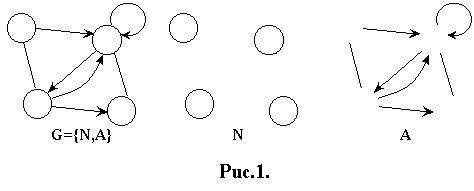 етью (графом) G может быть назван любой объект, который можно представить как совокупность множества узлов N и множества дуг A, соединяющих их. G  {N, A}. Каждый элемент множества A есть пара (i, j) элементов множества N. Примеры графического представления сетей и задающих их множеств см. рис. 1.

Узлы также называют вершинами или точками, а дуги - ребрами, звеньями, линиями или ветвями. Граф G конечен, если конечны оба задающие его множества N и A.

Сеть (граф) G₁, состоящую из узлов и дуг, входящих в сеть G, называют подграфом сети G; то есть G₁  {N₁, A₁} - подграф G  {N, A}, если N₁ N и A₁ A. Наиболее простое представление сети получается, если использовать в качестве элементов {N}натуральные числа - номера узлов. Тогда каждая дуга характеризуется парой чисел - номерами узлов, которые она связывает.

Однако каждый узел и дуга сети характеризуются еще одной числовой величиной, смысл которой определяется в конкретных задачах. В общем случае такое поставленное в соответствие узлу число называют его интенсивностью d. Узлы называют источниками (если d > 0), стоками (если d < 0) и нейтральными узлами (если d  0). Таким образом: N  {N_} {N_-} {N_o}; N_  {n : d_n > 0}, N_-  {n : d_n < 0}, N_o  {n : d_n  0}.

Аналогично, поставленное в соответствие дуге (i, j) число той же природы, что и интенсивность узла, называют пропускной способностью дуги r_ij.

Потоком F  {f_ij : (i, j) A} в сети G называют совокупность величин f_ij - потоков в дугах, удовлетворяющих соотношениям:

f_ij - f_ji  d_i, i N; 0  f_{ij } r_ij. (1)

Здесь первое выражение отражает закон сохранения потока в сети, а второе задает допустимую область изменения потоков в дугах. Во многих задачах на сетях для каждой дуги вводят дополнительную числовую характеристику - обобщенную стоимость c_ij прохождения единицы потока по дуге, не имеющую аналога для узлов. В таком случае может быть поставлена задача об оптимальном по суммарной обобщенной стоимости потоке:

c_ij f_ij  opt (2)

при одновременном выполнении условий (1). В результате эта задача принимает вид стандартной задачи линейного (если c_ij  const), либо нелинейного (если c_ij  F (f_kl), (k, l) A) программирования.

При решении задач в дальнейшем будут упоминаться методы и алгоритмы.

Метод - путь, способ получения решения; совокупность приемов, операций, направленных на достижение некоторой цели.

Алгоритм - последовательность четко определенных правил (команд) для получения решения за конечное число шагов.

Любой алгоритм - метод; но не любой метод является алгоритмом.